Radiálne zaťaženie Ako sa vypočítava, vyriešené cvičenia

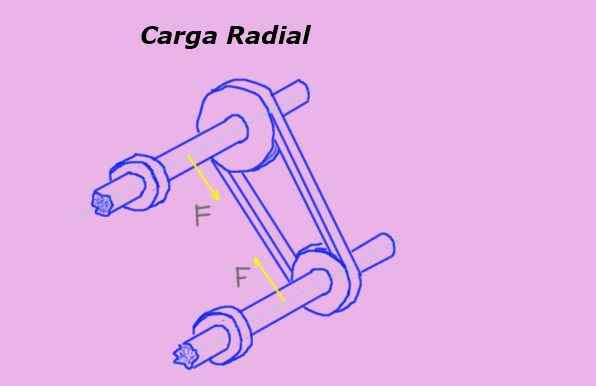
Ten Zaťaženie Je to sila, ktorá sa cvičí kolmo na os symetrie objektu a ktorej línia akcie prechádza touto osou. Napríklad pás na kladke ukladá radiálne zaťaženie ložiska alebo ložiska osi tej istej.

Na obrázku 1 žlté šípky predstavujú radiálne sily na osiach v dôsledku napätia pásu, ktorý prechádza cez remenice.

postava 1. Radiálne zaťaženie na osi kladky. Zdroj: Self Made.

Jednotka miery radiálneho zaťaženia v medzinárodnom systéme alebo ak je to Newton (n). Na jeho meranie sa však používajú aj iné silové jednotky, ako napríklad kilogramová sila (kg-f) a sila libry (LB-F).

[TOC]

Ako sa vypočítava? 

Na výpočet hodnoty radiálneho zaťaženia v prvkoch štruktúry sa musia dodržiavať nasledujúce kroky:

- Vytvorte schému síl na každom prvku.

- Uplatňovať rovnice, ktoré zaručujú translačný zostatok; to znamená, že súčet všetkých síl je nula.

- Zvážte rovnicu krútiacich momentov alebo momentov, aby sa splnila rotačná rovnováha. V tomto prípade musí byť suma všetkých krúžkov null.

- Vypočítajte sily na identifikáciu radiálnych zaťažení, ktoré pôsobia v každom z prvkov.

Vyriešené cvičenia

-Cvičenie 1

Nasledujúci obrázok zobrazuje kladku, cez ktorú prechádza napätá kladka s napätím T. Kladka je namontovaná na os, ktorá spočíva na dvoch chummacerách. Stred jedného z nich je vo vzdialenosti l₁ zo stredu kladky. Na druhom konci je druhá Chumacera, vo vzdialenosti l₂.

Môže vám slúžiť: Higroskopická: koncept, hygroskopické látky, príklady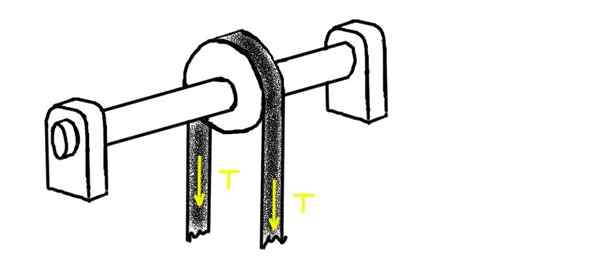Obrázok 2. Kladka, cez ktorú prechádza napätý popruh. Zdroj: Self Made.

Stanovte radiálne zaťaženie na každom z chummacerov, za predpokladu, že hmotnosť osi a kladky je pomerne nižšia ako aplikované napätie.

Berte ako hodnotu pre 100 kg-f napätie remienkov a pre vzdialenosti l₁= 1 ma l₂= 2 m.

Riešenie

V prvom rade sa vyrába diagram síl pôsobiacich na osi.

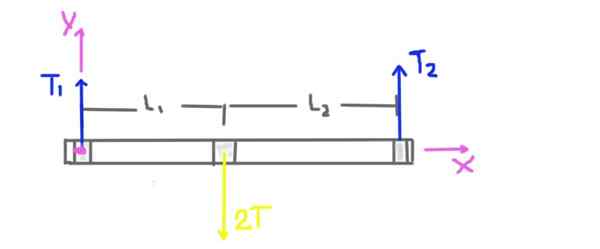Obrázok 3. Diagram cvičebných síl 1.

Napätie kladky je T, ale radiálne zaťaženie na osi v polohe kladky je 2T. Hmotnosť osi a kladky sa nezohľadňuje, pretože vyhlásenie o probléme nám hovorí, že je oveľa nižší ako napätie aplikované na pás.

Radiálna reakcia podpory podpory je spôsobená radiálnymi silami alebo zaťažením T1 a T2. Vzdialenosti L1 a L2 podpery v strede kladky sú tiež uvedené v diagrame.

Zobrazí sa aj súradnicový systém. Krútiaci moment alebo celkový moment na osi sa vypočíta ako centrum pôvodu súradníckeho systému a bude pozitívny v smere Z.

Rovnováha

Rovnovážné podmienky sú teraz stanovené: súčet rovnakej nuly a súčet krútiacich momentov sa rovná nule.

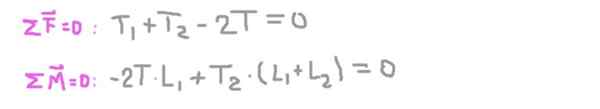
Z druhej rovnice radiálna reakcia na osi na podpere 2 (t₂), nahradenie v prvom a vyčistení radiálnej reakcie na osi na podpere 1 (t₁).

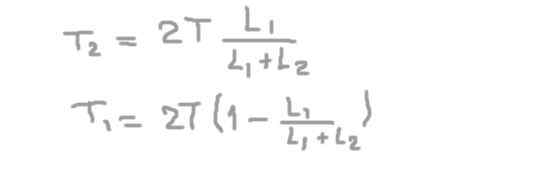Ak nahradíme numerické údaje, získame, že radiálne zaťaženie alebo sila na osi v polohe podpory 1 je:

Tón₁= (2/3) t = 66,6 kg-f

Môže vám slúžiť: Kalibračná krivka: Na čo je to, ako to urobiť, príklady

A radiálne zaťaženie osi na podpore podpory 2 je:

Tón₂= (4/3) t = 133,3 kg-f.

Cvičenie 2

Nasledujúci obrázok zobrazuje systém zložený z troch kladiek A, B, C všetky rádio R. Remenice sú spojené pásom, ktorý má napätie T.

Sekery A, B, C Pass MASICKÉ LOŽISKY. Oddelenie medzi centrami osí A a B je 4 -násobok polomeru r. Podobne je oddelenie osí B a C tiež 4R.

Stanovte radiálne zaťaženie osí kladiek A a B, za predpokladu, že napätie pásu je 600 N.

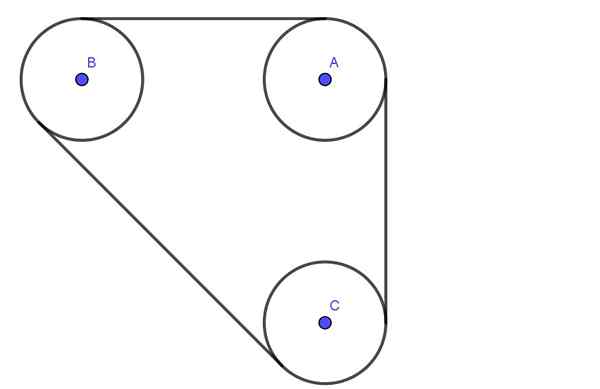Obrázok 4. Kladka. Cvičenie 2. (Vlastné rozpracovanie)

Riešenie

Začína sa nakreslením diagramu síl pôsobiacich na kladku A a B. Na prvom máte obidve napätie₁ a t₂, ako aj sila f_Do Že ložisko vyvíja na os kladke.

Podobne na kladke B máte napätie t₃ , Tón₄ a sila f_B že ložisko vyvíja na osi toho istého. Radiálne zaťaženie na osi kladky A je sila f_Do a radiálne zaťaženie na B je sila f_B.

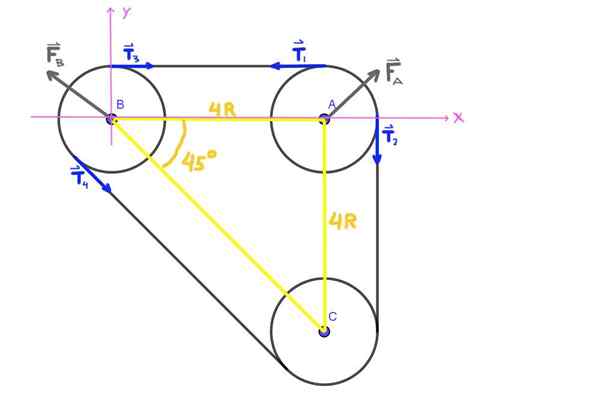Obrázok 5. Schéma síl, cvičenie 2. (Vlastné rozpracovanie)

Ako osi A, B, C tvoria trojuholník izorectangle, uhol ABC je 45 °.

Všetky napätia t₁ , Tón₂ , Tón₃ , Tón₄ zobrazené na obrázku majú rovnaký modul t, ktorým je napätie pásu.

Podmienka rovnováhy pre kladku a

Teraz píšeme rovnovážnu podmienku pre kladku, ktorej nie je nič iné ako súčet všetkých síl, ktoré konajú na kladke A, musia byť neplatné.

Oddelenie komponentov X a Y od síl a pridanie (vektorovo) Získa sa nasledujúci pár skalárnych rovníc:

Môže vám slúžiť: Titan (satelit)

F_DoX - T = 0; F_DoA - T = 0

Tieto rovnice vedú k nasledujúcej rovnosti: f_Sekera = F_Oh = T.

Preto má radiálne zaťaženie dané veľkosťou:

F_Do = (T² + t²)^1/2 = 2^1/2∙ t = 1,41 ∙ t = 848,5 n. Smer 45 °. 

Podmienka rovnováhy pre kladku B

Podobne píšeme rovnovážnu podmienku pre kladku B. Pre komponent X máte: f_BX + T + t ∙ cos45 ° = 0

A pre komponent y: f_BA + T ∙ sen45 ° = 0

Teda:

F_BX = - t (1+2^-1/2) a f_Podľa = -T ∙ 2^-1/2

To znamená, že veľkosť radiálneho zaťaženia na kladke B je:

F_B = ((1+2^-1/2) ² + 2^-1)^1/2∙ t = 1,85 ∙ t = 1108,66 n a jeho adresa je 135 °.

Odkazy

1. Beer F, Johnston E, Dewolf J, Mazurek, D. Mechanika materiálov. Piaty vydanie. 2010. MC Graw Hill. 1-130.
2. Gere j, goodno, b. Mechanika materiálov. Ôsme vydanie. Učenie sa. 4-220.
3. Giancoli, D. 2006. Fyzika: Princípy s aplikáciami. 6^Tth Edimatizovať. Sála. 238-242.
4. Hibbeler R. Mechanika materiálov. Ôsme vydanie. Sála. 2011. 3-60.
5. Valera Negrete, J. 2005. Všeobecné fyzikálne poznámky. Žobrák. 87-98.