Charakteristiky štvorca

Pravidelný štvorec. S licenciou

Hlavný Charakteristika štvorca Je to skutočnosť, že je tvorená štyrmi stranami, ktoré majú presne rovnaké opatrenia. Tieto strany sú organizované tak, aby tvorili štyri priame uhly (90 °).

On námestie Je to základná geometrická postava, objekt štúdie plochej geometrie, pretože je to dvojrozmerná postava (ktorá má širokú a vysokú, ale chýba mu hĺbka).

Štvorce sú polygóny. Konkrétnejším spôsobom sú to polygóny (a) štvoruholníky na to, aby mali štyri strany, b) rovnostranné prostriedky na strany, ktoré merajú to isté a c) rovníngulos pre uhly s rovnakou amplitúdou.

Tieto posledné dve vlastnosti štvorca (rovnostranný a rovnomerný) možno zhrnúť v jednom slove: pravidelné. To znamená, že štvorce sú pravidelnými štvornásobnými polygónmi.

Rovnako ako ostatné geometrické figúrky, štvorec má oblasť. Toto sa dá vypočítať vynásobením jednej zo svojich strán sama o sebe. Napríklad, ak máme štvorec, ktorý meria 4 mm, jeho oblasť bude 16 mm².

Štvorcové charakteristiky

1. Počet strán a rozmer

Štvorce sa skladajú zo štyroch strán, ktoré merajú rovnako. Okrem toho sú štvorce dve rozmerové postavy, čo znamená, že majú iba dve rozmery: široké a vysoké.

2. Polygón

Štvorce sú polygóny. To znamená, že štvorce sú geometrické čísla vymedzené uzavretou čiarou tvorenou po sebe idúcimi segmentmi čiary (uzavretá polygonálna čiara).

Konkrétne je to štvorstranný polygón, pretože má štyri strany.

3. Rovnostranný polygón

Hovorí sa, že polygón je rovnostranný, keď majú všetky jeho strany rovnaké opatrenie. To znamená, že ak jedna strana štvorca meria 2 metre, všetky strany zmerajú 2 metre.

Môže vám to slúžiť: Čo by sa stalo, keby bola Zem bližšie k slnku?

4. Polygón

Hovorí sa, že polygón je rovnomerným, keď všetky uhly, ktoré tvoria uzavretú polygonálnu čiaru, majú rovnaké opatrenie.

Všetky štvorce sú vyrobené zo štyroch priamych uhlov (tj 90 ° uhly), bez ohľadu na to.

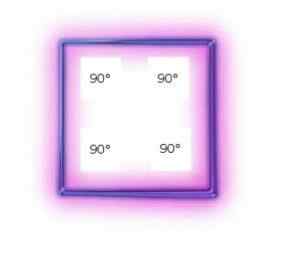
Všetky štvorce sú Equiangulos, pretože ich uhly majú rovnakú amplitúdu. To znamená 90 °.

5. Pravidelný polygón

Ak je polygón rovnostranný a zároveň v Estváre.

Pretože štvorec má strany, ktoré merajú rovnaké a uhly rovnakej amplitúdy, možno povedať, že ide o pravidelný mnohouholník.

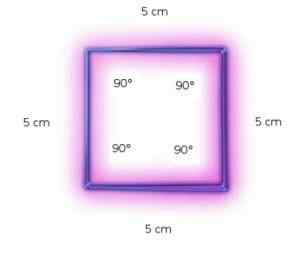
Štvorce majú obe strany rovnakej miery a uhly rovnakej amplitúdy, takže sú to pravidelné polygóny.

6. Oblasť štvorca

Oblasť štvorca sa rovná produktu na jednej strane na druhej strane. Pretože obe strany majú presne rovnaké opatrenie, vzorec sa dá zjednodušiť tvrdením, že oblasť tohto mnohouholníka sa rovná jednej zo svojich strán štvorcových, to znamená (bočné)².

Niektoré príklady výpočtu oblasti štvorca sú:

- Štvorec so stranami 2 m: 2 m x 2 m = 4 m²

- Štvorce so stranami 52 cm: 52 cm x 52 cm = 2.704 cm²

- Štvorec s 10 mm strany: 10 mm x 10 mm = 100 mm²

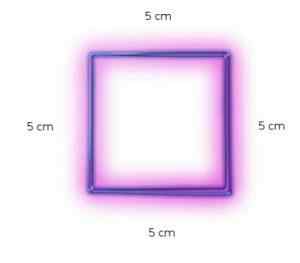
Štvorec prezentovaný na obrázku má 5 cm strany.

Vaša oblasť bude produktom 5 cm x 5 cm alebo čo je rovnaké (5 cm)²

Môže vám slúžiť: Hydrologia: Čo je, história, aké štúdie

V tomto prípade je štvorec štvorca 25 cm²

7. Štvorce sú rovnobežné logy

Paralegramy sú typom kvadrilaterálneho, ktoré majú dva páry paralelných strán. To znamená, že pár strán sa navzájom smeruje, zatiaľ čo to isté sa deje s ostatným krútiacim momentom.

Existujú štyri typy rovnobežní: obdĺžniky, kosoštvorc.

Štvorce sú rovnobežné logy, pretože majú dva páry strany, ktoré sú rovnobežné.

Strany (a) a c) sú rovnobežné.

Strany (b) a (d) sú rovnobežné.

8. Opačné uhly sú zhodné a po sebe idúce sa dopĺňajú

To, že dva uhly sú zhodné, znamená, že majú rovnakú amplitúdu. V tomto zmysle, keďže štvorec má všetky svoje uhly rovnakej amplitúdy, možno povedať, že opačné uhly sú zhodné.

Skutočnosť, že dva po sebe idúce uhly sú doplnkové, znamená, že súčet týchto dvoch sa rovná plochému uhlu (ten, ktorý má amplitúdu 180 °).

Uhly štvorca sú priame uhly (90 °), takže jeho súčet 180 °.

9. Sú postavené z obvodu

Na vybudovanie štvorca sa nakreslí obvod. Následne sa z tohto obvodu nakreslia dva priemery. Tieto priemery musia byť kolmé a vytvárajú kríž.

Akonáhle sa priemery vypracujú, budeme mať štyri body, v ktorých segmenty čiary znížili obvod. Ak sú tieto štyri body spojené, urobí sa štvorec.

10. Diagonály sú vyrezané v ich strede

Diagonálne sú priame čiary, ktoré sú nakreslené z uhla k inému, ktorý je oproti. Na štvorci je možné nakresliť dve diagonály. Tieto diagonály prechádzajú v strede námestia.

Môže vám slúžiť: Bibliografický výskum: Definícia, typy, techniky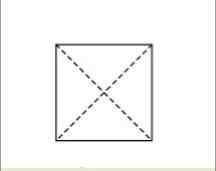

Na obrázku bodkované čiary predstavujú diagonály. Ako je zrejmé, tieto čiary prechádzajú presne uprostred štvorca.

Odkazy

1. Štvorcový a jeho vlastnosti. Zotavené z Mathonpenref.com
2. Vlastnosti kosoštvorcov, obdĺžnikov a štvorcov. Figuríny sa zotavili.com