Vektorové sumy

Čo sú vektorové sumy?

Ten Vektorové množstvo, alebo vektor, ako ten, pre ktorý je potrebné špecifikovať jeho veľkosť alebo modul (s príslušnými jednotkami) a ich adresa.

Na rozdiel od vektorového množstva má skalárne množstvo iba veľkosť (a jednotky), ale nie adresované. Niektoré príklady skalárnych množstiev sú okrem iného teplota, objem objektu, dĺžka, hmotnosť a čas.

Rozdiel medzi vektorovým množstvom a lezením

V nasledujúcom príklade sa môžete naučiť rozlíšiť skalárne množstvo od vektorového množstva:

Rýchlosť 10 km/h je skalárne množstvo, zatiaľ čo rýchlosť 10 km/h na sever je vektorové množstvo. Rozdiel je v tom, že v druhom prípade je špecifikovaná adresa, okrem veľkosti.

Vektorové množstvá majú nekonečno aplikácií, najmä vo svete fyziky.

Grafika a označenie vektorového množstva

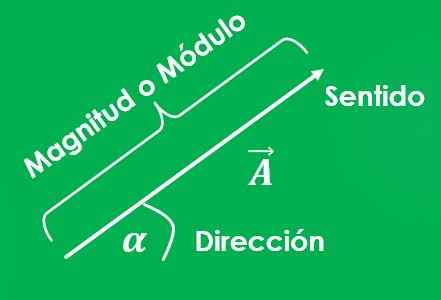
Spôsob, ako označiť vektorovú sumu, je umiestnenie šípky (→) na písmeno, ktoré sa má použiť, alebo písanie písmena tučným písmom (do).

Na graf vektorového množstva je potrebný referenčný systém. V tomto prípade sa karteziánska rovina použije ako referenčný systém.

Graf vektora je čiara, ktorej dĺžka predstavuje veľkosť; a uhol medzi uvedenou čiarou a osou x meraný v anti -horskom zmysle predstavuje jeho adresu.

Musí sa určiť, čo je východiskový bod vektora a aký je bod príchodu. Šípka je tiež umiestnená na konci čiary, ktorá ukazuje na bod príchodu, čo naznačuje, aký je smer vektora.

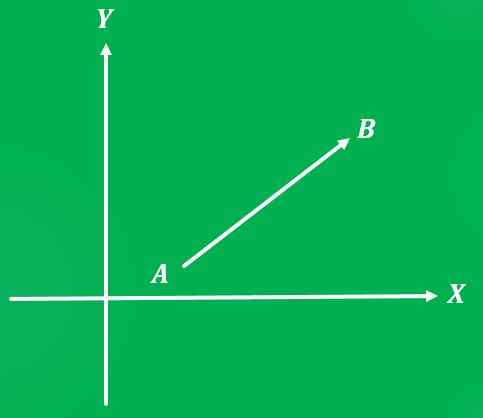
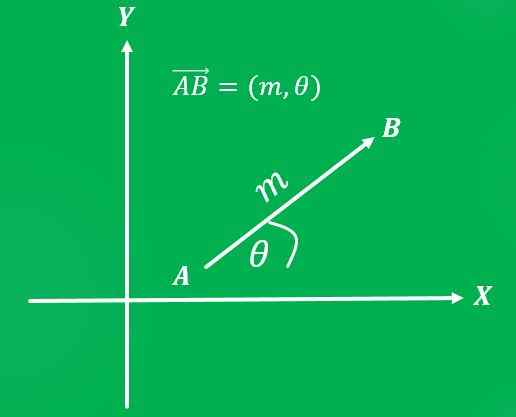
Akonáhle je referenčný systém nastavený, môžete napísať vektor ako usporiadaný pár: Prvá súradnica predstavuje jeho veľkosť a druhá súradnica jeho adresa.

Príklady vektorových sumy

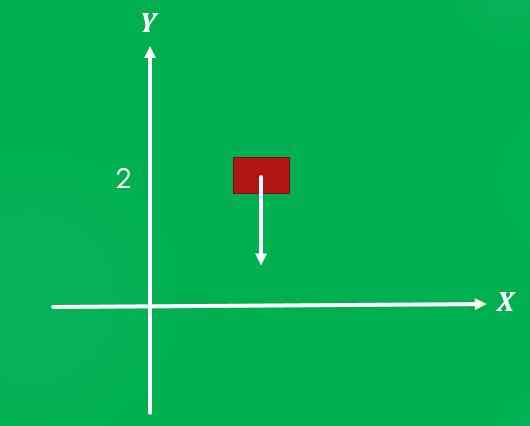
1- Gravitácia pôsobiaca na objekt

Ak je objekt umiestnený vo výške 2 metre nad zemou a uvoľňuje sa, gravitácia naň pôsobí s veľkosťou 9,8 m/s² a smerom kolmá na zem v smere.

2- Pohyb lietadla

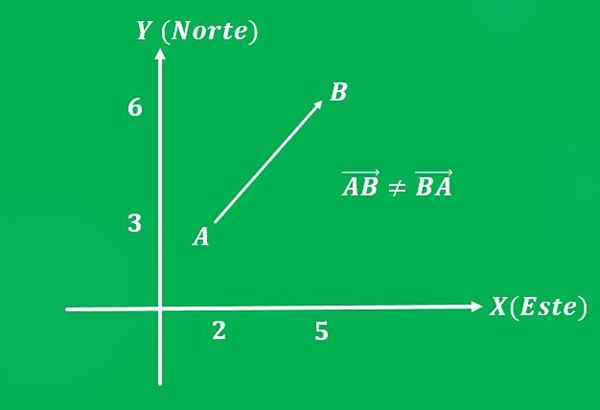
Rovina, ktorá sa pohybovala z bodu A = (2,3) do bodu B = (5,6) karteziánskej roviny, s rýchlosťou 650 km/h (veľkosť). Smer trajektórie je 45 ° na severovýchod (čo znamená).

Je potrebné poznamenať, že ak je objednávka obrátená, vektor má rovnakú veľkosť a rovnaký smer, ale iný význam, ktorý bude juhozápadný.

3- Sila aplikovaná na objekt

Juan sa rozhodne zatlačiť stoličku so silou 10 libier, v smere rovnobežne so zemou. Možné zmysly aplikovanej sily sú: vľavo alebo vpravo (v prípade karteziánskej roviny).

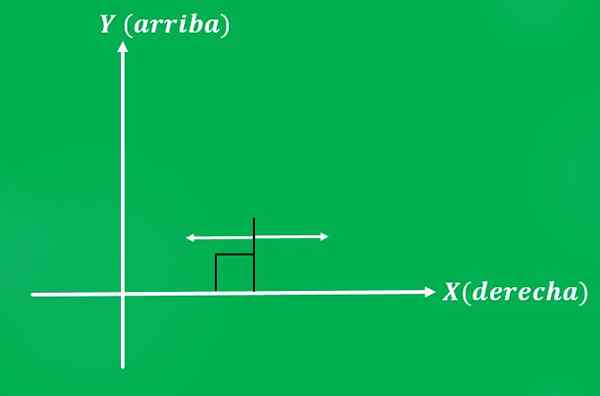
Rovnako ako v predchádzajúcom príklade význam, ktorý sa Juan rozhodne dať silu, prinesie iný výsledok.

To nám hovorí, že dva vektory môžu mať rovnakú veľkosť a smer, ale byť odlišné (prinášajú rôzne výsledky).

Je možné pridať a odpočítať dva alebo viac vektorov, pre ktoré existujú veľmi užitočné výsledky, napríklad zákon o rovnobežníku. Môžete tiež vynásobiť vektor skalárnym.