Koncept bezplatného konceptu, rovnice, cvičenia vyriešené

Ten voľný pád Je to vertikálny pohyb, ktorý objekt prežíva, keď je spadnutý z určitej výšky blízko povrchu Zeme. Je to jeden z najjednoduchších a najpriamejších pohybov, ktoré sú známe: v priamke a s konštantným zrýchlením.

Všetky objekty, ktoré sú vyhodené alebo ktoré sú vyhodené vertikálne nahor alebo nadol, sa pohybujú s zrýchlením 9.8 m/s² poskytnuté závažnosťou Zeme, bez ohľadu na jej hmotu.

Voľný pád z útesu. Zdroj: pexels.com.

Táto skutočnosť môže byť dnes akceptovaná bez problémov. Pochopenie skutočnej povahy voľného pádu však chvíľu trvalo. Gréci to už opísali a interpretovali veľmi v podstate smerom k štvrtému storočia.

[TOC]

Rovnice pohybu voľného pádu

Akonáhle je presvedčený, že zrýchlenie je rovnaké pre všetky telá uvoľnené pri pôsobení gravitácie, je čas zistiť potrebné rovnice na vysvetlenie tohto pohybu.

Je dôležité zdôrazniť, že v tomto prvom pohybe sa nezohľadňuje odpor vzduchu. Výsledky tohto modelu sú však veľmi presné a blízko reality.

Vo všetkom, čo nasleduje, bude predpokladať model častíc, to znamená, že rozmery objektu sa nezohľadňujú, za predpokladu, že celá hmotnosť je koncentrovaná v jednom bode.

Pre rovnomerne zrýchlený priamy pohyb sa považuje za osá na os a. Pozitívny zmysel je vzatý a negatívny dole.

Kinematické veľkosti

Týmto spôsobom sú rovnice polohy, rýchlosť a zrýchlenie v závislosti od času:

Zrýchlenie

A = g = -9.8 m/s² (-32 stôp/s²)

Pozícia v závislosti od času: a (t)

y = y_ani + vložka_ani . T + ½ GT²

Kde a kde_ani Je to počiatočná poloha mobilného mobilného telefónu a V_ani je počiatočná rýchlosť. Pamätajte, že pri vertikálnom spustení sa počiatočná rýchlosť nevyhnutne líši od 0.

Ktoré možno napísať ako:

a - a_ani = v_ani . T + ½ GT²

Δy = v_ani . T + ½ GT²

S δa byť posunom vyrobeným mobilnou časticou. V jednotkách medzinárodného systému sú pozícia aj posunutie uvedené v metroch (M).

Rýchlosť v závislosti od času: V (t)

v = v_ani + g . tón

Rýchlosť v závislosti od posunu

Je možné odvodiť rovnicu, ktorá spája posunutie rýchlosťou bez času na intervenciu času. Za týmto účelom sa vyčistí čas poslednej rovnice:

Môže vám slúžiť: kvantový mechanický model atómu

 A nahradí sa v rovnici posunu:

Δy = v_ani . T + ½ GT²

Štvorec je vyvinutý pomocou pozoruhodného produktu a výrazy sa preskupili.

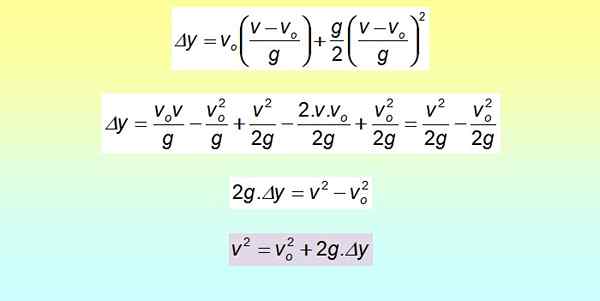
Táto rovnica je užitočná, keď čas nie je k dispozícii, ale namiesto toho existujú rýchlosti a posuny, ako bude vidieť v časti vyriešených príkladov.

Príklady voľného pádu

Pozorný čitateľ si všimne prítomnosť počiatočnej rýchlosti v_ani. Predchádzajúce rovnice sú platné pre vertikálne pohyby pod pôsobením gravitácie, keď objekt spadne z určitej výšky, akoby bol vyhodený vertikálne nahor alebo nadol.

Keď objekt klesne, je jednoducho hotový vložka_ani = 0 a rovnice sa zjednodušujú nasledovne.

Zrýchlenie

A = g = -9.8 m/s² (-32 stôp/s²)

Pozícia v závislosti od času: a (t)

y = y_ani+ ½ GT²

Rýchlosť v závislosti od času: V (t)

v = g . tón

Rýchlosť v závislosti od posunu

vložka² = 2G. D Y

D Y Bude to tiež negatívne, odvtedy vložka² Musí to byť kladná suma. Stane sa to tak, ak pôvod ani nula súradnicového systému v štartovom bode alebo na zemi.

Ak ho čitateľ uprednostňuje, môže sa vydať smerom nadol ako pozitívny. Gravitácia bude naďalej konať, ak sa predpokladá, že je + 9.8 m/s². Musíte však byť v súlade s vybranými značnými dohovorom.

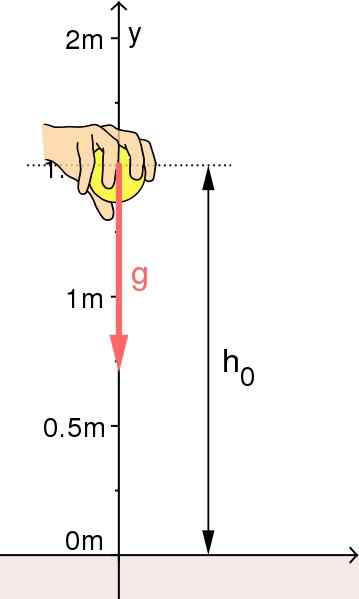Voľný pád objektu: Pôvod referenčného systému bol vybraný na zemi. Zdroj: Zdroj: Mikerun [CC BY-SA 4.0 (https: // creativeCommons.Org/licencie/By-SA/4.0)]

Vertikálne spustenie

Tu samozrejme nemôže byť počiatočná rýchlosť null. Musíme poskytnúť objekt pre impulz, ktorý by mohol ísť hore. Podľa poskytnutej počiatočnej rýchlosti sa objekt zvýši na väčšiu alebo menšiu výšku.

Samozrejme, bude okamih, keď sa objekt na chvíľu zastaví. Potom sa dosiahne maximálna výška vzhľadom na štartovací bod. Tiež zrýchlenie je stále dole. Pozrime sa, čo sa stane v tomto prípade.

Výpočet dosiahnutej maximálnej výšky

Výber ma = 0:

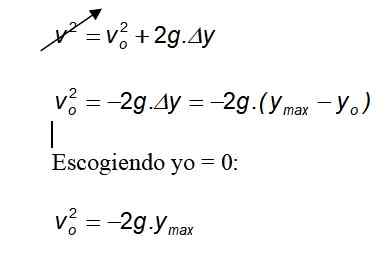
Keď gravitácia vždy ukazuje na zem v zápornom smere, záporné znamienko je zrušené.

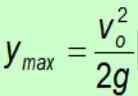
Maximálny časový výpočet

Podobný postup slúži na nájdenie času, ktorý potrebuje, aby objekt dosiahol maximálnu výšku.

v = v_ani + g . tón

Robí v = 0

vložka_ani = - g . tón_Maximálny

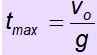
Čas letu je čas, ktorý objekt vydrží vo vzduchu. Ak sa objekt vráti do východiskového bodu, čas nárastu sa rovná času zostupu. Preto je čas letu 2. T max.

Môže vám slúžiť: mikroskopická stupnica: vlastnosti, počítanie častíc, príklady

Je dvakrát T T_Maximálny Celkový čas, ktorý objekt vydrží vo vzduchu? Áno, pokiaľ sa objekt začína od bodu a vráti sa k nemu.

Ak je uvedenie na trh vykonané z určitej výšky na zemi a objekt sa k tomu môže pokračovať, čas letu už nebude dvakrát väčší ako maximálny čas.

Vyriešené cvičenia

V rozlíšení nasledujúcich cvičení sa bude brať do úvahy nasledujúce:

1-výška, odkiaľ je predmet vyhodený, je malá v porovnaní s polomerom Zeme.

2-odpor vzduchu je opovrhnutý.

3-Hodnota zrýchlenia gravitácie je 9.8 m/s²

4-čo sú to problémy s jedným mobilom, najlepšie sa vyberie a_ani = 0 vo východiskovom bode. To zvyčajne uľahčuje výpočty.

5-na menší ako naopak, je uvedený smer nahor sa považuje za pozitívny.

6 -V stúpajúcich a zostupných kombinovaných pohyboch rovnice, ktoré sa použijú priamo, ponúkajú správne výsledky, pokiaľ sa konzistencia udržiava so znakmi: pozitívne, dole negatívne a závažnosť -9.8 m/s² alebo -10 m/s² Ak uprednostňujete zaokrúhlenie (pre viac pohodlia pri výpočte).

Cvičenie 1

Guľa sa vyhodí zvisle s rýchlosťou 25.0 m/s. Odpovedaj na nasledujúce otázky:

a) Koľko to stúpa?

b) ako dlho trvá, kým sa dosiahne najvyšší bod?

c) ako dlho trvá lopta, aby sa dotkla povrchu Zeme po dosiahnutí svojho najvyššieho bodu?

d) Aká je vaša rýchlosť, keď sa vrátite na úroveň, kde sa začala?

Riešenie

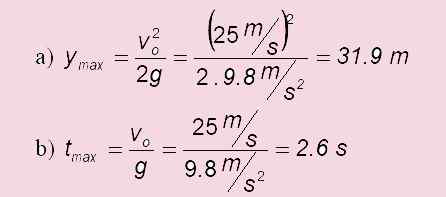
c) V prípade spustenia úrovne: tón_let = 2 . tón_Maximálny = 2 x6 s = 5.1 s

d) Keď sa vráti do východiskového bodu, rýchlosť má rovnakú veľkosť ako počiatočná rýchlosť, ale opačný smer, preto musí byť - 25 m/s. Ľahko sa skontroluje nahradením hodnôt v rovnici rýchlosti:

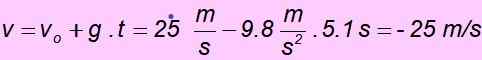
Cvičenie 2

Z vrtuľníka, ktorý zostupuje s konštantnou rýchlosťou 1, sa uvoľňuje malý poštový kufor.50 m/s. Po 2.00 s vypočítať:

a) Aká je rýchlosť kufra?

b) ako ďaleko je kufor pod vrtuľníkom?

c) Aké sú vaše odpovede na oddiely a) a b) ak vrtuľník stúpa konštantnou rýchlosťou 1.50 m/s?

Riešenie

Oddiel a

Pri opustení vrtuľníka je preto kufrí vložka_ani = -1.50 m/s. S uvedeným časom sa rýchlosť zvýšila vďaka zrýchleniu gravitácie:

Môže vám slúžiť: nebeské telá

v = v_ani + g . t = -1.50 - (9.8 x 2) m/s = - 21.1 m/s

Oddiel B

Pozrime sa, koľko kufra zostúpila vzhľadom na východiskový bod v tom čase:

Kufor: Dy = v_ani . T + ½ GT² = -1.50 x 2 + ½ (-9.8) x 2² M = -22.6 m

Bolo vybrané a_ani = 0 Na začiatku, ako je uvedené na začiatku sekcie. Záporné znamenie naznačuje, že kufor zostúpil 22. 6 m pod východiskovým bodom.

Medzitým vrtuľník Upadlo rýchlo -1.50 m/s, predpokladáme neustále, preto v uvedenom čase 2 sekundy, vrtuľník cestoval:

Vrtuľník: δy = v_ani.t = -1.päťdesiat x 2 m = -3 m.

Preto sú kufor a vrtuľník po 2 sekundách oddelené vzdialenosťou od:

D =| -22.6 - (-3) | M = 19. 6 m.

Vzdialenosť je vždy pozitívna. Na zdôraznenie tejto skutočnosti sa používa absolútna hodnota.

Oddiel C

Keď vrtuľník stúpa, má rýchlosť + 1.5 m/s. S touto rýchlosťou vyjde kufor, takže po 2 s už nosí:

v = v_ani + g . T = +1.50 - (9.8 x 2) m/s = - 18.1 m/s

Ukázalo sa, že rýchlosť je negatívna, pretože po 2 sekundách sa kufor pohybuje nadol. Sa zvýšila vďaka gravitácii, ale nie toľko ako v časti a.

Teraz zistíme, koľko kufra zostúpila s ohľadom na východiskový bod počas prvých 2 sekúnd cestovania:

Valija: δy = v_ani . T + ½ GT² = +1.50 x 2 + ½ (-9.8) x 2² M = -16 .6 m

Medzitým vrtuľník Zastával Pokiaľ ide o východiskový bod a urobil to konštantnou rýchlosťou:

Vrtuľník: δy = v_ani.T = +1.päťdesiat x 2 m = +3 m.

Po 2 sekundách sú kufor a vrtuľník oddelené vzdialenosťou od:

D =| -16.6 - (+3) | M = 19.6 m

Vzdialenosť, ktorá ich oddeľuje, je v oboch prípadoch rovnaká. Kufor cestuje v druhom prípade menej vertikálnu vzdialenosť, pretože jej počiatočná rýchlosť bola nasmerovaná nahor.

https: // youtu.be/w2uvetxwsfk

Odkazy

1. Kirkpatrick, L. 2007. Fyzika: pohľad na svet. 6^{ubytovať sa} Skrátene vydanie. Učenie sa.  23 - 27.
2. Rex, a. 2011. Základy fyziky. Pearson. 33 - 36
3. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14^th. Edimatizovať. Objem1. 50 - 53.
4. Serway, r., Vulle, C. 2011. Základy fyziky. 9^nat Edimatizovať. Učenie sa. 43 - 55.
5. Wilson, J. 2011. Fyzika 10. Pearson Vzdelanie. 133 - 149.