Konjugovaný binomický, ako je vyriešený, príklady, cvičenia

A Konjugovaný binomický Z iného binomialu je ten, v ktorom sa líšia iba znakom operácie. Binomén, ako už názov napovedá, je algebraická štruktúra, ktorá pozostáva z dvoch termínov.

Niektoré príklady binomiálov sú: (A + b), (3m - N) a (5x - y). A ich príslušné konjugované binomialy sú: (a - b), (-3m - n) a (5x + y). Ako je vidieť okamžite, rozdiel je v znamení.

postava 1. Binomický a jeho konjugovaný binomén. Majú rovnaké výrazy, ale líšia sa v znamení. Zdroj: f. Zapata.

Binomén znásobený jeho konjugátom vedie k pozoruhodnému produktu, ktorý sa veľa používa v algebre a vede. Výsledkom množenia je odčítanie štvorcov pojmov pôvodného binomialu.

Napríklad, (X - y) Je binomický a jeho konjugát je (x + y). Potom je produkt týchto dvoch binomiálov rozdielom štvorcov pojmov:

(X - y).(x + y) = x² - a²

[TOC]

Ako je vyriešený konjugovaný binomén?

Pravidlo stanovené s konjugovanými binomialmi je nasledujúce: 

Produkt dvoch konjugátových binomiálov sa rovná štvorcovi prvého obdobia mínus štvorca druhého funkčného obdobia. Tento výsledok sa nazýva štvorcový rozdiel.

Ako príklad aplikácie začneme preukázaním predchádzajúceho výsledku, ktorý sa dá urobiť pomocou distribučnej vlastnosti produktu vzhľadom na algebraic sum.

(x - y) (x + y) = x.x + x.a - a.X - y.a

Predchádzajúce násobenie sa získalo podľa týchto krokov:

- Prvé funkčné obdobie prvého binomialu sa vynásobí prvým funkčným obdobím druhého

- Potom prvý z prvého, druhý z druhej

- Potom druhý z prvého prvého z druhej 

- Nakoniec druhý z prvého pre druhú druhú.

Môže vám slúžiť: Vektorová algebra

Teraz urobme malú zmenu pomocou komunistického majetku: a.x = x.a. Zostáva to takto:

(x - y) (x + y) = x.x + x.y - x.a - a.a

Pretože existujú dva rovnaké výrazy, ale inak (zvýraznené vo farbe a podčiarknutí), sú zrušené a zjednodušené:

(x - y) (x + y) = x.X - y.a

Nakoniec sa uplatňuje, že vynásobenie čísla samo osebe je rovnocenné s jeho zdvíhaním štvorca, tak X.x = x² a tiež a.y = y².

Týmto spôsobom sa v predchádzajúcej časti zdôraznilo, že produktom súčtu pre jeho rozdiel je rozdiel štvorcov:

(X - y).(x + y) = x² - a²

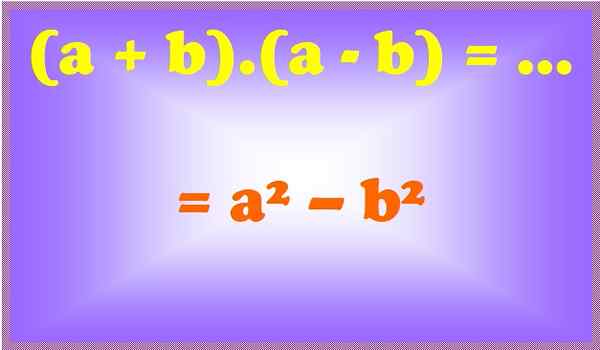Obrázok 2. Suma pre jeho rozdiel je rozdiel štvorcov. Zdroj: f. Zapata.

Príklady

- Konjugované binomialy rôznych výrazov

Príklad 1

Nájdite konjugát (a² - 3y).

Odpoveď: (a² + 3y)

Príklad 2

Získajte produkt (a² - 3y) pre jeho konjugát.

Odpoveď: (a² - 3y) (a² + 3y) = (a²)² - (3y)² = y⁴ - 3² a² = y⁴ - 9y²

Príklad 3

Vyvíjať produkt (1 + 2a).(2a -1).

Odpoveď: Predchádzajúci výraz je ekvivalentný (2a + 1).(2a -1), to znamená, že zodpovedá produktu binomialu pre jeho konjugát.

Je známe, že produkt binomialu pre jeho konjugovaný binomén sa rovná rozdielu štvorcov binomických výrazov:

(2a + 1) (2a -1) = (2a)² - 1² = 4 a² - 1

Príklad 4

Napíšte produkt (x + y + z) (x - y - z) ako rozdiel štvorcov.

Odpoveď: Trinomiály môžeme asimilovať pred formou konjugovaných binomiálov, čím dôkladne využívajú zátvorky a štvorcové držiaky:

(x + y + z) (x - y - z) = [x + (y + z)] [x - (y + z)]

Týmto spôsobom je možné uplatniť rozdiel štvorcov:

(x + y + z) (x - y - z) = [x + (y + z)].[x - (y+z)] = x² - (Y+z)²

Príklad 5

Vyjadriť produkt (m² - m -1).(m² + m -1) ako rozdiel v štvorci.

Môže vám slúžiť: 120 deliteľov

Odpoveď: Predchádzajúci výraz je produktom dvoch trinomiálov. Po prvé, musí byť prepísaný ako produkt dvoch konjugovaných binomialov:

(m² - m -1) (m² + m -1) = (m² - 1 - m) (m² -1 + m) = [(m² -1) - M].(M² -1) +m)]

Uplatňujeme skutočnosť, že produkt binomialu jeho konjugátom je kvadratickým rozdielom v jeho podmienkach, ako je vysvetlené:

(M² -1) - M].(M² -1) +m)] = (m² -1)² - m²

Cvičenia

Ako vždy, začína to najjednoduchšími cvičeniami a potom zvyšuje úroveň zložitosti.

- Cvičenie 1

Escrida (9 - a²) ako produkt.

Riešenie

Najprv prepíšeme výraz ako rozdiel štvorcov, aby sme použili to, čo vysvetlilo predtým. Preto:

(9 - a²) = (3² - do²)

Okamžite faktorom, čo je rovnocenné s písaním tohto rozdielu štvorcov ako produktu, ako sa požaduje vo vyhlásení:

(9 - a²) = (3² - do²) = (3 + a) (3 -a)

- Cvičenie 2

Faktorizovať 16x² - 9y⁴.

Riešenie

Faktor a výraz znamená písať ako produkt. V tomto prípade je potrebné predtým prepísať expresiu, aby sa získal rozdiel štvorcov.

Nie je ťažké to urobiť, pretože starostlivo pozorovanie, všetky faktory sú perfektné štvorce. Napríklad 16 je štvorec 4, 9 je štvorec 3, a⁴ je štvorec a² a X² je štvorec X:

16x² - 9y⁴  = 4²X² - 3²a⁴ = 4²X²  - 3²(a²)²

Potom, čo už vieme, je aplikované: že rozdiel v štvorci je produktom konjugovaných binomialov:

(4x)² - (3 a²)² = (4x - 3 a²) . (4x + 3 a²)

- Cvičenie 3

Napíšte (a - b) ako binomický produkt

Riešenie

Predchádzajúci rozdiel by sa mal napísať ako štvorcové rozdiely

(√a)² -(√b)²

Potom sa aplikuje, že rozdiel v štvorci je produktom konjugovaných binomiálov

Môže vám slúžiť: zníženie podobných výrazov

(√a - √b) (√a + √b)

- Cvičenie 4

Jedným z použití konjugovaného binomialu je racionalizácia algebraických výrazov. Tento postup spočíva v eliminácii koreňov menovateľa frakčného výrazu, ktorý pri mnohých príležitostiach uľahčuje operácie. Žiada sa, aby použil konjugovanú binomiálnu hodnotu na racionalizáciu nasledujúceho výrazu:

√ (2 -x) / [√3 - √ (2+x)]]]]]]]

Riešenie

Prvým je identifikácia konjugovaného binomického menovateľa: [√3 + √ (2 + x)]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]].

Teraz znásobujeme čitateľ a menovateľ pôvodného expresie konjugovaným binomiálnym prúdom:

√ (2 -x) [√3+√ (2+x)] /[√3 - √ (2+x)].[√3 + √ (2 + x)]

V menovateľovi predchádzajúceho výrazu rozpoznávame produkt rozdielu súčtom, ktorý už vieme, že zodpovedá rozdielu štvorcov binomiálov:

√ (2-x) .[√3 + √ (2 + x)] /(√3)² - [√ (2+x)]² 

Zjednodušenie menovateľa je:

√ (2-x).[√3+√ (2+x)] / [3 - (2+x)] = √ (2 -x). [√3 + √ (2 + x)] / (1 - x)

Teraz sa staráme o čitateľa, pre ktorý budeme uplatňovať distribučnú vlastnosť produktu s ohľadom na sumu:

√ (2-x) .[√3 + √ (2 + x)] / (1 - x) = √ (6-3x) + √ [(2 -x) (2 + x)] / (1 - x)

V predchádzajúcej expresii rozpoznávame produkt binomického (2-x) pre jeho konjugát, čo je pozoruhodný produkt rovnajúci sa rozdielom štvorcov. Týmto spôsobom sa konečne získa racionalizovaný a zjednodušený výraz:

[√ (6-3x) + √ (4-x²)] / (1 - x)

- Cvičenie 5

Vypracujte nasledujúci produkt pomocou vlastností konjugovaného binomialu:

[2^{(x + 3y)} - Tretí^{(x - 3y)}].[2^{(x + 3y)} + Tretí^{(x - 3y)}]

Riešenie

4^{(2x + 6y)} - 9^{(2x - 6y)} = 4a^(2x) .do^(6y) - 9^(2x) .do^(-6y)= [4a^(6y) - 9^(-6y)] .do^(2x)

Pozorný čitateľ si všimne spoločný faktor, ktorý bol zvýraznený farbou.

Odkazy

1. Baldor, a. 1991. Algebra. Venezuelské kultúrne redaktory.Do.
2. González J. Konjugované binomické cvičenia. Zotavené z: akadémie.Edu.
3. Matematika Alex. Pozoruhodné výrobky. Obnovené z YouTube.com.
4. Matematika. Konjugované binomialy/ významné výrobky. Obnovené z YouTube.com.
5. Konjugované binomické výrobky. Získané z: LMS.Colbachenlinea.mx.
6. Obdivovaný. Konjugované binomialy. Obnovené z: YouTube.com.