Antidevačné vzorce a rovnice, príklady, cvičenia

A antidevatívny F (x) funkcia Fx) sa tiež nazýva primitívny alebo jednoducho neurčitý integrál uvedenej funkcie, ak v danom intervale Jo, Je pravda, že F '(x) = f (x)

Zoberme si napríklad nasledujúcu funkciu:

f (x) = 4x³

Antiderivative tejto funkcie je f (x) = x⁴, Pretože odvodením F (x) pravidlom derivácie pre právomoci:

Sa získava presne f (x) = 4x³.

Je to však iba jeden z mnohých antiderivátov F (x), pretože táto ďalšia funkcia: g (x) = x⁴ + 2 Je to tiež, pretože odvodením g (x) vzhľadom na x je to isté, získané späť f (x).

Skontrolujme to:

Pamätajte, že ten odvodený z konštanty je 0. Preto do termínu x⁴ Môžete pridať akúkoľvek konštantu a jej derivát bude naďalej 4x³.

Dospelo sa k záveru, že akákoľvek funkcia všeobecnej formy f (x) = x⁴ + C, kde C je skutočná konštanta, slúži ako antiderivácia F (x).

Predchádzajúci ilustratívny príklad možno vyjadriť takto:

df (x) = 4x³ Dx

Nedefinovaný antidevatívny alebo integrál je vyjadrený so symbolom ∫, preto:

F (x) = ∫4x³ dx = x⁴ + C

Kde funkcia f (x) = 4x³  To sa nazýva integrácia, a C je Konštanta.

[TOC]

Príklady antiderivátov

postava 1. Anti -hotley nie je ničím iným ako neurčitým integrálom. Zdroj: Pixabay.

Nájdenie antiderivácie funkcie je jednoduché v niektorých prípadoch, keď sú deriváty dobre známe. Napríklad je to funkcia f (x) = sen x, uniderivovaná pre ňu je iná funkcia f (x), takže pri odvodení sa získa f (x).

Táto funkcia môže byť:

F (x) = - cos x

Skontrolujme, či je to pravda:

F '(x) = (- cos x)' =- (-sen x) = sin x

Preto môžeme napísať:

∫sen x dx = -cos x + c

Okrem poznania derivátov existujú základné a jednoduché pravidlá integrácie na nájdenie neurčitého antidevatívneho alebo integrálneho.

Môže vám slúžiť: následné deriváty

Buďte skutočnou konštantou:

1.- ∫kdx = k ∫dx = kx + c

2.- ∫kf (x) dx = k ∫f (x) dx

Ak je možné funkciu H (x) vyjadriť ako súčet alebo odčítanie dvoch funkcií, potom je jeho neurčitý integrál:

3.- ∫h (x) dx = ∫ [f (x) ± g (x)] dx = ∫f (x) dx ± ∫g (x) dx

Toto je vlastnosť linearity.

Ten Výkon Pre integrály sa dá zriadiť týmto spôsobom:

Toto pravidlo má zjavné obmedzenie: od menovateľa N +1 To nedá urobiť 0, teda n ≠ -1.

V prípade n = -1 sa používa toto pravidlo:

5.- ∫X ^-1 Dx = ln x +c

Je ľahké preukázať, že derivát Ln x Je to presne X ^-1.

Diferenciálne rovnice

Diferenciálna rovnica je taká, v ktorej je neznáma ako derivát.

Teraz, z predchádzajúcej analýzy, je ľahké si uvedomiť, že inverzná operácia derivátu je nedefinovaná antidevatívna alebo integrálna.

Nech f (x) = y '(x), to znamená odvodené z určitej funkcie. Na označenie tohto derivátu môžeme použiť nasledujúci zápis:

To okamžite nasleduje:

dy = f (x) dx

Neznámym z diferenciálnej rovnice je funkcia y (x), ktorá je derivátom F (x). Na jeho vyčistenie je predchádzajúci výraz integrovaný na obidvoch stranách, čo je ekvivalentné uplatňovaniu antiderivatívnych:

∫dy = ∫f (x) dx

Ľavý integrál je vyriešený integračným pravidlom 1, s k = 1, a preto je vyhľadávaný -awaite vyčistený:

a (x) = ∫f (x) dx = f (x) + c

A keďže C je skutočná konštanta, aby som vedel, čo je v každom prípade vhodné, vyhlásenie musí obsahovať dostatok ďalších informácií na výpočet hodnoty C. Toto sa volá Úvodná podmienka.

Uvidíme príklady toho všetkého v nasledujúcej časti.

Môže vám slúžiť: Prebužný odhad

Antidevidované cvičenia

- Cvičenie 1

Uplatňujte pravidlá integrácie na získanie nasledujúcich nedefinovaných antideitív alebo integrálov uvedených funkcií, čo čo najviac zjednodušuje výsledky. Je vhodné overiť výsledok deriváciou.

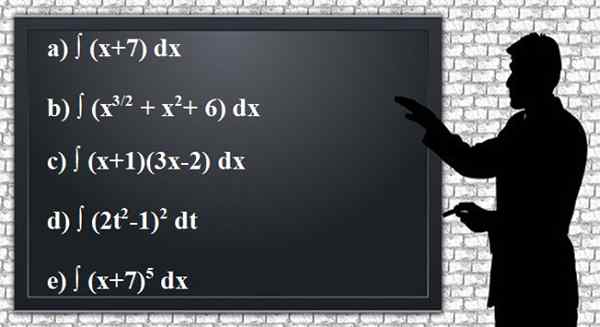Obrázok 2. Definované predné alebo integrálne cvičenia. Zdroj: Pixabay.

Roztok

Najprv uplatňujeme pravidlo 3, pretože integrácia je súčet dvoch výrazov:

∫ (x +7) dx = ∫ xdx +∫7dx

Pre prvý integrál sa uplatňuje pravidlo právomocí:

∫ xdx = (x² /2)+C₁

V druhom integrálnom pravidle 1 sa uplatňuje, je k = 7:

∫7dx = 7∫dx = 7x + c₂

A teraz sa pridávajú výsledky. Tieto dve konštanty sú zoskupené do jednej, všeobecne nazývané C:

∫ (x+7) dx = (x² /2) + 7x + c

Riešenie B

Linearity sa tento integrálny rozkladá do troch jednoduchých integrálov, na ktoré sa bude uplatňovať pravidlo právomocí:

∫ (x^3/2 + X² + 6) dx = ∫x^3/2 Dx + ∫x² dx +∫6 dx =

= (2/5) x^5/2 + (1/3) x³ + 6x + c

Všimnite si, že pre každého integrálu sa objaví integračná konštanta, ale stretávajú sa v jednom volaní C.

Riešenie c

V tomto prípade je vhodné uplatniť distribučnú vlastnosť násobenia na vývoj integrácie. Potom použijete pravidlo právomocí na nájdenie každého integrálu osobitne, ako v predchádzajúcom roku.

∫ (x+1) (3x-2) dx = ∫ (3x²-2x+3x-2) dx = ∫ (3x² + X - 2) dx

Pozorný čitateľ bude pozorovať, že dva centrálne výrazy sú podobné, preto sa pred integráciou znížia:

∫ (x+1) (3x-2) dx = ∫3x² dx + ∫ x dx + ∫- 2 dx = x³ + (1/2) x² - 2x + c

Riešenie e

Spôsob, ako vyriešiť integrál, by bolo vyvinúť silu, ako sa to stalo v príklade D. Avšak, keď je exponent vyšší, bolo by potrebné vykonať premennú zmenu, takže nemusíte robiť taký dlhý vývoj.

Môže vám slúžiť: Kontinuálna náhodná premenná

Zmena premennej je nasledovná:

U = x + 7

Odvodenie na oboch stranách Tento výraz:

du = dx

Integrál sa transformuje na jednoduchšiu s novou premennou, ktorá je vyriešená pravidlom právomocí:

∫ (x+7)⁵ Dx = ∫ u⁵ du = (1/6) u⁶ + C

Nakoniec sa zmena vráti a vráti sa do pôvodnej premennej:

∫ (x+7)⁵ Dx = (1/6) (x+7)⁶ + C

- Cvičenie 2

Častica je spočiatku v pokoji a pohybuje sa pozdĺž osi x. Jeho zrýchlenie pre t> 0 je dané funkciou a (t) = cos t. Je známe, že pri t = 0 je pozícia x = 3, všetko v jednotkách medzinárodného systému. Žiada sa, aby sa našla rýchlosť v (t) a poloha x (t) častice.

Riešenie

Pretože zrýchlenie je prvý odvodený z rýchlosti vzhľadom na čas, máte nasledujúcu diferenciálnu rovnicu:

a (t) = v '(t) = cos t

Z toho vyplýva:

v (t) = ∫ cos t dt = sin t + c₁

Na druhej strane vieme, že rýchlosť je zase derivátom polohy, preto sa znova integrujeme:

x (t) = ∫ v (t) dt = ∫ (sin t + c₁) dt = ∫sen t dt + ∫c₁ dt = - cos t + c₁ t + c₂

Integračné konštanty sú určené z informácií uvedených vo vyhlásení. Najprv hovorí, že častica bola spočiatku v pokoji, preto V (0) = 0:

V (0) = sin 0 + c₁ = 0

C₁ = 0

Potom musíte x (0) = 3:

x (0) = - cos 0 + c₁ 0 + c₂ = - 1 + c₂ = 3 → c₂ = 3+1 = 4

Funkcie rýchlosti a polohy sú určite také:

v (t) = sen t

x (t) = - cos t + 4

Odkazy

1. Engler, a. 2019. Integrálny počet. Národná univerzita pobrežia.
2. Larson, R. 2010. Výpočet premennej. 9NA. Vydanie. McGraw Hill.
3. Bezplatné matematické texty. Antiderivát. Získané z: matematiky.Libretexts.orgán.
4. Wikipedia. Antidevatívny. Zdroj: In.Wikipedia.orgán.
5. Wikipedia. Neurčitá integrácia. Obnovené z: je.Wikipedia.orgán.