Definícia zrýchlenia centripetalu, vzorce, výpočet, cvičenia

Ten zrýchlenie do_c, Tiež sa nazýva radiálne alebo normálne, je to zrýchlenie, ktoré nesie mobilný objekt pri opise kruhovej trajektórie. Jeho veľkosť je vložka²/r, kde r Je to polomer kruhu, je nasmerovaný do stredu jeho stredu a je zodpovedný za to, aby mobil zostal na svojej trase.

Rozmery zrýchlenia centripetálu sú dĺžka za jednotku času. V medzinárodnom systéme sú m/s². Ak z nejakého dôvodu zmizne zrýchlenie centripetálne.

Revolvingové objekty majú centripetálne zrýchlenie, ktoré je nasmerované do stredu trajektórie. Zdroj: Pixabay

To sa stane s autom, ktoré sa snaží dať krivku na plochej a mrazovej dráhe, pri ktorej trenie medzi podlahou a kolesami je nedostatočné, aby auto vzalo krivku. Preto jediná možnosť, že ste zostali, je pohybovať sa v priamke, a preto sa dostanete z krivky.

[TOC]

Kruhové pohyby

Keď sa objekt pohybuje v kruhu, vždy je zrýchlenie centripetálu radiálne nasmerované do stredu obvodu, smer, ktorý je kolmý na trajektóriu.

Pretože rýchlosť je vždy dotyčená do trajektórie, takže rýchlosť a centripetálne zrýchlenie sa ukázalo ako kolmo. Preto rýchlosť a zrýchlenie nemajú vždy rovnaký smer.

Za týchto okolností má mobil možnosť opísať obvod konštantnou alebo variabilnou rýchlosťou. Prvý prípad je známy ako jednotný alebo kruhový pohyb MCU svojou skratkou, druhým prípadom bude variabilný kruhový pohyb.

Môže vám slúžiť: Čo je to emisné utierky? (S príkladmi)

V obidvoch prípadoch je zrýchlenie centripetálneho zrýchlenia zodpovedné za udržiavanie mobilného krúžku a zaberajú, že rýchlosť sa líši iba v smere a smerovaní.

Avšak, aby ste mali variabilný pohyb kruhu, bola by potrebná ďalšia zložka zrýchlenia v rovnakom smere rýchlosti, ktorá je zodpovedná za zvýšenie alebo znižovanie rýchlosti. Táto zložka zrýchlenia je známa ako Tangenciálne zrýchlenie.

Variabilný kruhový pohyb a zakrivený pohyb vo všeobecnosti majú obidve zložky zrýchlenia, pretože krivočiary pohyb si dokáže predstaviť ako trasa cez nespočetné oblúky obvodov, ktoré tvoria zakrivenú trajektóriu.

Centripetálna sila

Teraz je sila zodpovedná za zabezpečenie zrýchlenia. Pre satelit, ktorý obieha Zem, je to sila gravitácie. A keďže gravitácia vždy pôsobí kolmá na trajektóriu, nezmení rýchlosť satelitu.

V tomto prípade gravitácia pôsobí ako a dostredivá sila, že to nie je špeciálna trieda alebo okrem sily, ale v prípade satelitu je radiálne nasmerovaná do stredu Zeme.

V iných typoch kruhového pohybu, napríklad automobilu, ktorý má krivku, je úloha centripetálnej sily interpretovaná statickou silou rubb, ktorá núti mobil otočiť.

Vzorce pre centripetálne zrýchlenie

Centripetálne zrýchlenie sa vypočíta výrazom:

Ac = vložka²/r

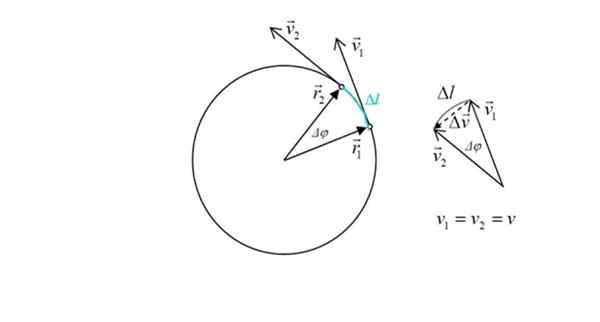Schéma na výpočet zrýchlenia centripetálu v mobile s MCU. Zdroj: Zdroj: Ilevanat [CC BY-SA 3.0 (https: // creativeCommons.Org/licencie/By-SA/3.0)]

Tento výraz sa odvodí nižšie. Zrýchlenie je podľa definície variáciou rýchlosti v čase:

Môže vám slúžiť: Svetelné zdroje: Typy a zariadenia, ktoré vyžarujú svetlo

Horný diagram zobrazuje na ľavom obrázku, dva body, cez ktoré mobilný mobilný telefón prechádza, ktorý sa pohybuje po rádiovom kruhu r V zmysle antihorária. Všimnite si, že veľkosť rýchlosti je v oboch prípadoch rovnaká, ale nie smer alebo význam.

Mobilný používa čas δtón Na prehliadke, ktorá je malá, pretože body sú veľmi blízko.

Obrázok tiež zobrazuje dva polohové vektory r₁ a r₂, ktorého modul je rovnaký: rádio r obvodu. Uhol medzi oboma bodmi je δφ. V zelenej klonovať sa Prehliadka mobilu, označená ako ΔL.

Na obrázku napravo je zrejmé, že veľkosť δvložka, Zmena rýchlosti je približne úmerná AL, pretože uhol δφ je malý. Ale zmena rýchlosti súvisí presne na zrýchlenie. Trojuholník je varovaný sumou vektorov, ktoré:

vložka₁ + Δvložka = vložka₂ → δv = v₂ - vložka₁

Δvložka Je to zaujímavé, pretože je úmerné centripetálnemu zrýchleniu. Z obrázku je varované, že byť malý uhol Δφ, vektor δvložka Je to v kolmej podstate oboje vložka₁ Páči sa mi to vložka₂ a ukazuje na stred obvodu.

Aj keď vektory vynikajú tučným písmom, pre účinky geometrickej povahy, ktoré nasledujú, pracujeme s modulmi alebo veľkosťami týchto vektorov, bez ohľadu na vektorový zápis.

Niečo iné: Musíte použiť definíciu centrálneho uhla, čo je:

Δφ= Δl/r

Teraz sa porovnávajú obe čísla, ktoré sú úmerné od uhla δφ je to bežné:

Môže vám slúžiť: Čo je polarizované svetlo?

 

Rozdelenie medzi Δt:

 Pretože definíciou rýchlosti je v = ΔL/ Δt. Ale δV/ Δtón Je to presne rozsah centipetálneho zrýchlenia, čo sa hľadá. Týmto spôsobom sa dosiahne výraz opísaný na začiatku:

do_c= v²/r

Cvičenie

Častica sa pohybuje v kruhu 2.70 m rádio. V určitom čase je jeho zrýchlenie 1.05 m/s² V smere, ktorý robí uhol 32.0 ° s riaditeľstvom hnutia. Vypočítajte svoju rýchlosť:

a) V tom čase

b) 2.00 sekúnd neskôr za predpokladu konštantného tangenciálneho zrýchlenia.

Odpoveď

Je to rozmanitý kruhový pohyb, pretože vyhlásenie naznačuje, že zrýchlenie má daný uhol so smerom pohybu, ktorý nie je alebo 0 ° (nemohol to byť kruhový pohyb) alebo 90 ° (bol by to rovnomerný kruhový pohyb).

Preto dve zložky - radiálne a tangenciálne - koexistujú. Bude označený ako_c už_tón a javí sa nakreslený na nasledujúcom obrázku. Zelený vektor je čistý vektor zrýchlenia alebo jednoducho zrýchlenie do.

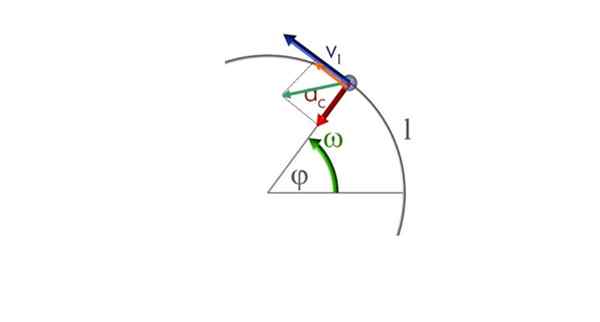Častica sa pohybuje v kruhovej trajektórii v antihorárnom zmysle a rôznorodý pohyb kruhu. Zdroj: Commons.Wikimedia.orgán

a) Výpočet komponentov zrýchlenia

do_c = a.cos θ = 1.05 m/s² . cos 32.0 ° = 0.89 m/s² (v červenej)

do_tón = a.hriech θ = 1.05 m/s² . Sen 32.0 ° = 0.57 m/s² (v oranžovej)

Výpočet mobilnej rýchlosti

Od a_c = vložka²/r, tak:
b) 2 sekundy neskôr rýchlosť vložka sa zvýši vďaka tangenciálnej zložke zrýchlenia

v = v_ani +do_tón. T = 1.6 m/s + (0.57 x 2) m/s = 2.74 m/s

Odkazy

1. Giancoli, D. Fyzika. 2006. Zásady s aplikáciami. Šieste vydanie. Sála. 107-108.
2. Hewitt, Paul. 2012. Koncepčná fyzická veda. Piaty vydanie.Pearson.106 - 108.