X na druhú

Vysvetľujeme, čo je X na druhé, jeho vlastnosti, príklady a cvičenia vyriešené

Oblasť štvorca „x“ strany je X na druhej strane. Zdroj: f. Zapata.

Algebraická prevádzka “X na druhú„Vykonáva sa vynásobením množstva„ x “dvakrát. Je súčasťou potenciálnych operácií a v matematických symboloch sa vyjadruje týmto spôsobom:

x ∙ x = x²

Toto je konkrétny prípad posilnenia, v ktorom „x“ predstavuje základňa A „2“ je exponent. Ak sa v operácii zobrazí termín X², Znie presne ako „X Squared“ alebo „X Square vyvýšené“.

Prirodzene sú možné ďalšie exponenty, napríklad, ak je exponent 3, potom je sila napísaná ako:

x ∙ x ∙ x = x³

A čítajte ako „x na tri“, „X zdvihnuté na kocku“ alebo jednoducho „x do kocky“.

Všeobecne platí, že exponent, na ktorý je základňu vysoký, môže byť akékoľvek číslo, nazývané „N“, a v takom prípade je napísaný príslušná sila:

Xⁿ = x ∙ x ∙ x ∙… ∙ x

Tu podnetové body naznačujú, že „x“ sa musí vynásobiť samotným „N“, to znamená toľkokrát, ako to naznačuje exponent.

Niekoľko jednoduchých príkladov „X Squared“ s číslami sú nasledujúce:

3² = 3 ∙ 3 = 9

(−4)² = (−4) ∙ (−4) = 16

Neskôr sú opísané rôzne aplikácie, pre ktoré je to potrebné.

Potenciálne vlastnosti

Všeobecne platí, že produkt akéhokoľvek sumy sám so sebou, n krát sa nazýva potenciácia. Výpočet X na druhej strane je iba konkrétny prípad zosilnenia, dva ďalšie prípady sa objavia, keď chcete zvýšiť sumu na exponent 1, čo v dôsledku toho získava rovnakú sumu:

Môže vám slúžiť: zákony exponentov

Pretože tieto operácie sú časté, spolupracovať so základňami a exponentmi, dodržiavajú sa niektoré jednoduché prevádzkové pravidlá, ktoré sa nazývajú Zákony exponentov, ktoré sú uvedené nižšie:

Zákony exponentov

V nasledujúcom texte sú exponenty „X“ a „n“ a „m“.

1.- Produkt rovnakých základných síl

Vynásobením dvoch (alebo viacerých) síl rovnakej bázy sa získa základňa zvýšená na súčet exponentov:

Xⁿ∙ x^m = x^n+m

V prípade x vysokých sa toto pravidlo uplatňuje nasledovne a nahradí N a M za 1:

X¹∙ x¹ = x¹⁺¹ = x²

2.- Divízia právomocí rovnakej základne

Rozdeľovaním sily tej istej základne sa získa základňa, zvýšená na odčítanie medzi príslušnými exponentmi čitateľa a menovateľom:

Xⁿ ÷ x^m = x^N-m

Pretože delenie 0 nie je definované, musí sa splniť za predpokladu, že x ≠ 0.

3.- Sila

Výsledok výkonu energie sa rovná základne zvýšenej na produkt exponentov:

(X^m)ⁿ = x^m∙n

Je možné získať znova x štvorcový, keď robíte m = 1 a n = 2:

(X¹)² = x^1∙2 = x²

4.- Negatívny exponent

Pre negatívnych exponentov je operácia, ktorá sa má vykonať,:

Kedykoľvek x ≠ 0. Všimnite si, že v tomto prípade sa sila stáva zlomkom s čitateľom rovnajúcim sa 1.

5.- Frakčný exponent

Frakčné exponenty môžu byť napísané ako koreň základne:

Pod podmienkou, že n sa líši od 0. Táto hodnota sa stáva koreňovým indexom, zatiaľ čo m sa stáva exponentom množstva pod koreňom, čo je v tomto prípade x.

Môže vám slúžiť: čo je usmernenie? (Geometria)

Výrobky a kvocienty rôznych základní

Ak musíte vylepšiť produkty a kvocienty rôznych základní „X“ a „Y“, dodržiavajú sa tieto pravidlá:

1.- Výkonnosť produktu

Na vykonanie tejto sily sa každá suma zvýši na exponent n a výsledný produkt je stanovený:

(x ∙ y)ⁿ = xⁿ ⋅ aⁿ

2.- Pomer kvocientu

Opäť sa musí každá suma zvýšiť na exponent n osobitne a stanoviť kvocient, ktorý výsledkom je podľa pravidla, že suma „y“ sa líši od 0, v prípade pozitívneho „N“:

(x ÷ y)ⁿ = xⁿ ÷ yⁿ

Ak je „n“ negatívny, musí sa venovať opatrnosť, z dôvodu majetku 4 predchádzajúcej časti sa čitateľ stáva menovateľom. V takom prípade sa obe sumy musia líšiť od 0, pretože deleniu o 0 sa treba za každú cenu vyhnúť.

Príklady

Príklad 1: Štvorce prírodných čísel

Štvorce prvých desiatich prírodných čísel sú:

• 1²= 1 × 1 = 1
• 2²= 2 × 2 = 4
• 3²= 3 × 3 = 9
• 4²= 4 × 4 = 16
• 5²= 5 × 5 = 25
• 6²= 6 × 6 = 36
• 7²= 7 × 7 = 49
• 8²= 8 × 8 = 64
• 9²= 9 × 9 = 81
• 10²= 10 × 10 = 100

Príklad 2: Štvorec záporných čísel

Štvorec záporného čísla je vždy pozitívny, pretože sa teda vynásobia dve sumy rovnakého znaku:

(-x) · (-x) = x ∙ x = x²

Napríklad:

(-2) · (-2) = (-2)² = 4

Príklad 3: Square sumy a rozdielu

Často je potrebné vypočítať štvorec súčtu dvoch množstiev alebo jeho rozdielov, ktoré sú zahrnuté v kategórii významných výrobkov.

Operácia je vyriešená s uvedenými indikáciami a pomocou distribučnej vlastnosti:

Štvorec

Nechajte dve sumy „x“ a „y“ a vy chcete nájsť štvorec svojej sumy (x + y)²:

Môže vám slúžiť: hierarchia operácií

(x + y)² = (x + y) ∙ (x + y) = x ∙ x + x ∙ y + y ∙ x + y ∙ y = x² + 2x ∙ y + a²

Tento výraz znie takto: „Square prvého plus dvojitý produkt prvého pre druhý plus štvorec druhého“.

Štvorcový rozdiel

Je to vyriešené analogicky, ale berúc do úvahy negatívne znamenie:

(x - y)² = (x - y) ∙ (x - y) = x ∙ x - x ∙ y + y ∙ x - y ∙ y = x² - 2x ∙ a + a²

Príklad 4: Oblasť štvorca

Štvorec je 4 -vedený polygón, ktorý má rovnaké opatrenie. Nech ℓ je bočné meranie, potom oblasť A obrázku je daná:

A = ℓ²

Príklad 5: Pythagorasova veta

Táto veta sa vzťahuje na obdĺžnikové trojuholníky, na ktorých dve strany tvoria rovný uhol. Tieto strany sú známe ako „kategórie“ a zvyšná strana je „hypotenus“.

Veta ustanovuje, že štvorec hypotenusa sa rovná súčtu štvorcov kategórií. Veta je napísaná „A“ a „B“ do kategórií a „C“ k hypotenuse, veta je napísaná ako:

c² = a² + b²

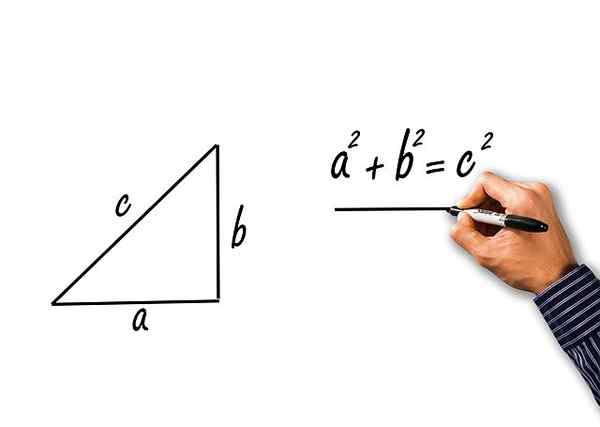Pythagorská veta pre obdĺžnikový trojuholník mačiek A a B a hypotenusa c

Vyriešené cvičenia

Cvičenie 1

Vypočítajte štvorec hypotenusu, ktorého nohy merajú 3 a 5 jednotiek.

Riešenie

Podľa Pythagorasovej vety je štvorec hypotenusu:

c² = a² + b²

Výmena hodnôt:

c² = 3² + 5²= (3 × 3) + (5 × 5) = 9 + 25 = 34

Cvičenie 2

Stanovte plochu bočného štvorca ℓ = 6 cm

Riešenie

A = ℓ² = (6 cm)² = 36 cm²