Zväzok

Vysvetľujeme, aký je objem, jeho vzorce, jednotky, ako ich vypočítať a uviesť niekoľko príkladov

Aký je objem?

On zväzok tela je numerická hodnota, ktorá meria množstvo priestoru, ktorý je obsadený. Vysoká, šírka a hĺbka určujú objem, čím väčší, čím väčší je okupovaný priestor.

Koncept objemu je veľmi dôležitý, pretože svet je trojrozmerný a všetky objekty majú šírku, výšku a hĺbku, preto majú objem. Ľudia ho často používajú, napríklad odhadom, či nábytok, ktorý chcú kúpiť, zapadá do svojej izby alebo či vstúpia do určitej veľkosti oblečenia.

V určitých oblastiach vedy a inžinierstva, napríklad pri práci s tekutkami, či užmi kvapalina alebo plyny, obsadený objem získava veľký význam: Pri plnení kontajnerov a čerpacích kvapalín, ako je voda, alebo pri návrhu lode pre loď, aby ste sa uistili Neopadneš. To všetko je nevyhnutné určiť to pre mnoho procesov.

Existujú vzorce na výpočet objemu geometrických telies v pravidelných tvaroch, ako sú hranoly, gule, valce a kužele, napríklad v závislosti od niektorých jeho rozmerov. A existujú aj spôsoby, ako zistiť objem nepravidelných objektov, ako bude opísané o niečo neskôr.

Objemové vzorce v geometrických číslach

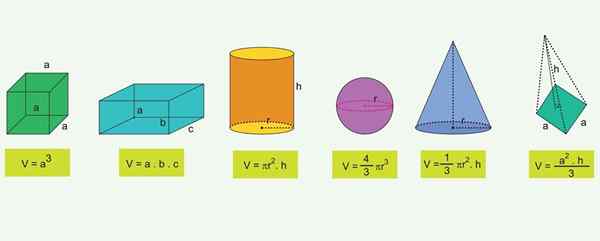Zoznam najbežnejších geometrických čísel a vzorec ich zväzkov

Pre najznámejšie geometrické objekty existujú vzorce, ktoré umožňujú vypočítať jeho objem:

• Kocka

V = ℓ³ 

Kde v predstavuje objem a ℓ je okraj (strana) kocky.

• Rovnobežný

Paralepiped je obdĺžnikový box so šírkou „a“, dlhá ℓ a „h“ výška. Jeho objem je daný produktom svojich troch rozmerov:

V = a ∙ ℓ ∙ h

• Sféra

Objem gule závisí od jej polomeru R:

Môže vám slúžiť: Nicolás Copernico

• Kruhový valec

Objem rovného kruhového valca je produkt medzi plochou jeho základne a výškou „H“. Pretože základňa je rozhlasový album „R“, ktorého oblasť je a = π · r², Zväzok zostáva:

V = πr²∙ h

• Kunda

Objem kužeľa je tretina produktu medzi plochou kruhovej bázy A a výškou H. Ako a = πr², tak:

• Pyramída

Pre pyramídu, ktorej základná oblasť je a má výšku „H“, je objem daný:

Ak má pyramída štvorcový základ na strane „A“, ako na obrázku, základná plocha základne je² A objem pyramídy je:

V = (1/3) ⋅a²⋅h

• Hranol

Objem hranolu je produkt medzi oblasťou základne A a výškou „H“:

V = a ∙ h

Objemové jednotky

V medzinárodnom systéme jednotiek je jednotkou pre objem kubický meter alebo m³, Zatiaľ čo v anglo -saxonovom systéme je to kubická noha alebo ft³ (z Nohy, čo v angličtine znamená „nohu“).

Existuje mnoho ďalších jednotiek podľa veľkosti okupovaného priestoru. Napríklad kubické kilometre kubické³ Pre väčšie objemy alebo kubické milimetre mm³ Pre malé zväzky. Existujú aj jednotky miestneho používania.

Je tiež potrebné spomenúť kapacitné jednotky, úzko súvisiace s objemovými jednotkami, ktoré sa najlepšie používajú pre kvapaliny. Jednotka centrálnej kapacity je liter, skrátená L, ktorá je rovnocenná s DM³ (Kubický decimeter).

Ostatné jednotky, ktoré sa oplatí spomenúť, sú galón, kubický palec, šálka a dna, ktoré sa používali na dávku liekov.

Môže vám slúžiť: porovnávacia metóda

Ako sa meria objem?

Objem tela, rovnako ako akékoľvek iné opatrenie, sa vykonáva v porovnaní s primeraným vzorom, v tomto prípade jednotka objemu.

Objemová jednotka je definovaná ako kocka, ktorej hrana meria 1 jednotku. Táto jednotka môže byť meter, centimeter, noha, palec alebo akékoľvek iné. Potom objem objektu zodpovedá množstvu kubických jednotiek obsadených obrázkom a je vždy kladným množstvom.

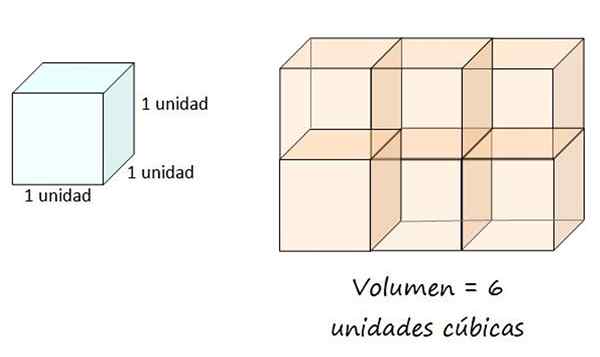Kubická jednotka je definovaná ako objem vedra s okrajom rovnajúcou sa 1, takže políčka vpravo má objem 6 kubických jednotiek. Zdroj: f. Zapata.

Objem geometrického tela

Pokiaľ ide o geometrické telo, ako už bolo uvedené, objem sa vypočíta prostredníctvom príslušného vzorca, ktorý merá rozmery označené vzorcom.

Napríklad, ak chcete poznať objem gule, je potrebné zmerať jej priemer a je známy jeho polomer, čo je polovica. Ak ide o obdĺžnikový box, meria sa šírka, výška a hĺbka.

Potom sa vložia hodnoty požadované vo vzorci, pričom sa dá pozor, aby všetky jednotky boli rovnaké, požadované operácie sa vykonávajú, existuje objem objektu.

Objem nepravidelného tela

Nepravidelné tuhé látky nemajú geometrický tvar, napríklad kameň alebo žmurknutie. Napriek tomu nájdete jeho objem pomocou absolventovanej nádoby plnej vody pomocou metódy posunu kvapaliny.

V prvom rade je určený objem obsadený vodou a potom je nepravidelný objekt úplne ponorený a meria nový objem, ktorý je väčší ako pôvodný. Objem nepravidelného objektu je rozdiel medzi týmto objemom a objemom vody samotnej.

Môže vám slúžiť: Genie Wiley, divoké dievča, ktoré len poznalo jej meno

Aby táto metóda fungovala, objekt by nemal byť vyrobený z žiadnej látky, ktorá sa ľahko rozpustí vo vode, musí zostať úplne ponorená a samozrejme musíte mať odstupňovaný nádobu potrebnej veľkosti, aby ste ju úplne prispôsobili.

Objemové príklady

Približný objem niektorých známych objektov je:

• Zem: 1,08321 × 10¹² km³
• Rieka Amazonas: 225.000 m³/s (objem na jednotku času sa nazýva „tok“)
• Veľká pyramída Gízy: 2.600.000 m³
• Futbalový loptička: 5600 cm³
• Batoh: 50 dm³

Objem a hmotnosť

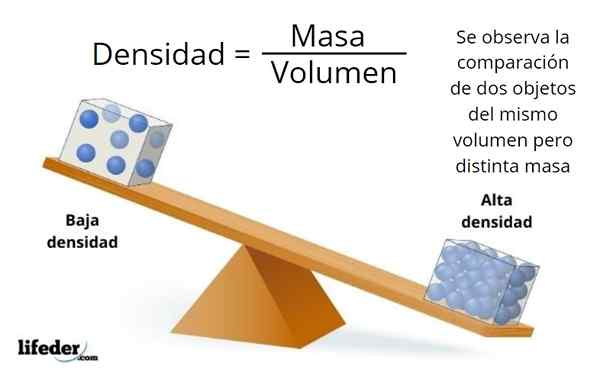
Objem a hmotnosť nie sú synonymá, prvé sú spojené s rozmermi objektu a druhým k množstvu hmoty, ktorú obsahuje.

V objekte malých rozmerov môže byť veľa hmoty alebo veľmi málo vo veľkom predmete, ktorý závisí od hustoty materiálu, čo je pomer medzi hmotnosťou a objemom objektu:

Vyriešené cvičenia

Cvičenie 1

Vypočítajte objem obdĺžnikovej škatule, ktorej rozmery sú 34 cm x 22 cm × 8 cm.

• Riešenie

Objem obdĺžnikového boxu je jednoducho produktom jeho troch rozmerov:

Vložka = 34 cm x 22 cm × 8 cm = 5984 cm³

Cvičenie 2

Základ kvadrangulárnej pyramídy má plochu 16 cm² A jeho výška je 6 cm. Vypočítajte objem uvedenej pyramídy.

• Riešenie

Vyššie uvedený vzorec pre objem pyramídy sa používa, známa oblasť jej základne:

A číselné hodnoty sa vymieňajú:

V = (1/3) × 16 cm² × 6 cm = 32 cm³