Areolárna rýchlosť, ako sa vypočítava a vyriešite cvičenia

Ten Areolárna rýchlosť Je to zametacia oblasť na jednotku času a je konštantná. Je to typické pre každú planétu a vyplýva z opisu Keplerovho druhého zákona matematickým spôsobom. V tomto článku vysvetlíme, z čoho pozostáva a ako sa vypočíta.

Boom, ktorý predstavuje objav planét mimo slnečnej sústavy, reaktivoval záujem o planétový pohyb. Nič neverí, že tieto exo-planéty dodržiavajú iné zákony, ako sú už známe a platné pre slnečnú sústavu: Keplerove zákony.

Johannes Kepler bol astronómom, ktorý bez pomoci ďalekohľadu a používania pozorovaní svojho mentora Tycha Braheho vytvoril matematický model, ktorý popisuje pohyb planét okolo slnka.

Zanechal tento model vyjadrený v troch zákonoch, ktoré nesú jeho meno a ktoré zostávajú rovnako platné ako v roku 1609, keď založil prvé dva a 1618, dátum, kedy tretí.

[TOC]

Kepler zákony

V súčasnom jazyku hovoria Keplerove tri zákony takto:

1. Obežné dráhy všetkých planét sú eliptické a slnko je zamerané.

2. Vektor polohy, ktorý prechádza zo slnka na planétu, zametá rovnaké oblasti v rovnakých časoch.

3. Štvorec orbitálnej periódy planéty je úmerný kocke polopriepustnej elipsy opísanej elipsy.

Planéta bude mať lineárnu rýchlosť, ako každý známy objekt, ktorý sa pohybuje. A je toho viac: pri písaní Keplerovho druhého zákona v matematickej podobe, nový koncept nazývaný Areolar Speed, typická pre každú planétu.

Prečo sa planéty pohybujú elipticky okolo slnka?

Zem a ostatné planéty sa pohybujú okolo slnka vďaka skutočnosti, že na ne vyvíja silu: gravitačnú príťažlivosť. To isté platí pre akúkoľvek inú hviezdu a planéty, ktoré zodpovedajú vášmu systému, ak ich máte.

Môže vám slúžiť: citlivé teplo: koncept, vzorce a cvičenia vyriešené

Toto je sila typu známeho ako centrálna sila. Hmotnosť je ústrednou silou, s ktorou sú všetci oboznámení. Objekt, ktorý uplatňuje centrálnu silu, či už ide o slnko alebo vzdialená hviezda, priťahuje planéty smerom k ich stredu a pohybujú sa opisujúcou uzavretú krivku.

V zásade sa táto krivka môže aproximovať ako obvod, ako to urobil Nicolás Copernico, poľský astronómový tvorca heliocentrickej teórie,.

Zodpovedná sila je gravitačná príťažlivosť. Táto sila závisí priamo od masiek hviezdy a danej planéty a je nepriamo úmerná štvorcovi vzdialenosti, ktorá ich oddeľuje.

Problém nie je taký ľahký, pretože v slnečnej sústave všetky prvky interagujú týmto spôsobom a zvyšujú zložitosť tejto záležitosti. Nie sú to tiež častice, pretože hviezdy a planéty majú merateľnú veľkosť.

Z tohto dôvodu nie je centrálny bod obežnej dráhy alebo okruhu cestovaný planétami presne sústredenými na hviezdu, ale na bod známeho ako ťažisko systému sol-plany.

Výsledná obežná dráha je eliptická. Zobrazí ho nasledujúci obrázok, pričom ako príklad sa berie na zem a Slnko:

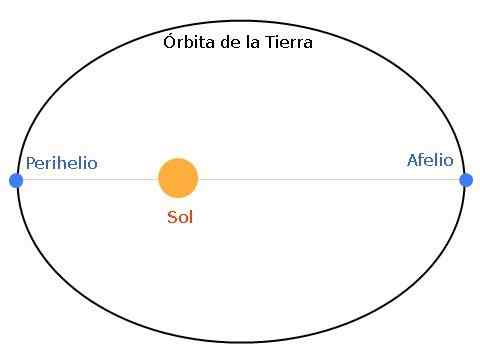postava 1. Obežná dráha Zeme je eliptická, pričom slnko sa nachádza v jednom z ohnísk. Keď sú Zem a slnko v maximálnej vzdialenosti, hovorí sa, že Zem je v afériu. A ak je vzdialenosť minimálna, hovoríme o Perihelio.

Apelium je najvzdialenejšou polohou od Zeme po slnko, zatiaľ čo perihelium je najbližším bodom. Elipsa môže byť viac -menej sploštená podľa charakteristík hviezdneho systému - planéta.

Hodnoty ASEL a Perihelio sa každoročne líšia, pretože ostatné planéty spôsobujú poruchy. Pre iné planéty sa tieto pozície nazývajú podpora a odborné znalosti.

Veľkosť lineárnej rýchlosti planéty nie je konštantná

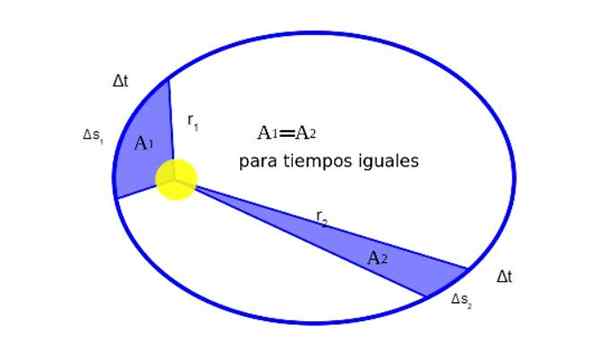
Kepler zistil, že keď planéta obieha okolo slnka, počas pohybu Barra rovnaké oblasti v rovnakých časoch. Obrázok 2 graficky zobrazuje význam tohto:

Môže vám slúžiť: Aká je rovnováha častíc? (S príkladmi)Obrázok 2. Pozícia vektora planéty vzhľadom na slnko je r. Keď planéta opisuje svoju obežnú dráhu, cestuje po elipse oblúk AS v čase ΔT.

Matematicky skutočnosť, že₁ rovnať sa₂ Vyjadruje sa takto:

Trasy oblúkov sú malé, takže každá oblasť sa môže priblížiť k oblasti trojuholníka:

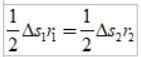
Ako δs =vložkaΔtón, Kde v je lineárna rýchlosť planéty v danom bode, pri výmene máme:

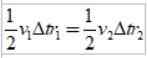
A keďže časový interval AT je rovnaký, získa sa:

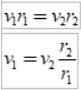
Ako r₂ > r₁, Potom v₁ > v₂, Inými slovami, lineárna rýchlosť planéty nie je konštantná. V skutočnosti je Zem rýchlejšie, keď je v periheliu, ako keď je v apheliu.

Preto lineárna rýchlosť Zeme alebo akejkoľvek planéty okolo slnka nie je veľkosťou, ktorá slúži na charakterizáciu pohybu uvedenej planéty.

Areolárna rýchlosť

Keplerov druhý zákon naznačuje novú veľkosť nazývanú areolárna rýchlosť. Je definovaný ako oblasť zametaná na jednotku času a je konštantná. Na jeho výpočet sa používa nasledujúci obrázok:

Obrázok 3. Vektor pozície Zeme (alebo planéta) vzhľadom na slnko je R a pri pohybe zem prežije posun, tiež vektor Δr.

Pri vykonávaní eliptického obvodu sa vyberie malá oblasť zametaná Zemou, čo označíme, ako ΔA. Čas potrebný na to je Δt.

Obrázok 3 zobrazuje vektor polohy Zeme vzhľadom na slnko, označený R. Keď sa Zem pohybuje, zažite vytesnenie ΔR.

Táto oblasť zodpovedá polovici oblasti obdĺžnika znázornenej na obrázku 3:

Kvocient AR/AT je presne lineárna rýchlosť Zeme, takže areolárna rýchlosť zostáva:

Vložka_Do V medzinárodnom systéme sú:

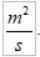
Všimnite si, že zatiaľ čo sa obidve R aj V líšia, produkt zostáva konštantný. To zmení areolárnu rýchlosť na veľmi vhodnú veľkosť na charakterizáciu pohybu planéty okolo jej hviezdy.

Môže vám slúžiť: Antoínové konštanty: vzorce, rovnice, príklady

Produkt R a V je veľkosť uhlovej hybnosti L, takže areolárna rýchlosť sa dá vyjadriť ako:

Výpočet lineárnej rýchlosti a areolárnej rýchlosti

S nasledujúcim príkladom ukážeme, ako vypočítať areolárnu rýchlosť, keď sú známe parametre planétového pohybu:

Cvičenie

Podľa Keplerových zákonov sa okolo Elliptickej obežnej dráhy pohybuje exo-planét okolo slnka. Keď je v experi, jeho rádiový vektor je r₁ = 4 · 10⁷ km, a keď je na podpore, je r₂ = 15 · 10⁷ km. Lineárna rýchlosť vo svojej odbornosti je V₁ = 1 000 km/s.

Vypočítať:

A) Rozsah rýchlosti v podpore.

B) Areolárna rýchlosť exo-planetu.

C) Dĺžka hlavnej semi -axie elipsy.

Odpoveď na)

Používa sa rovnica:

v ktorých sa nahradia číselné hodnoty.

Každý výraz je identifikovaný takto:

vložka₁ = Rýchlosť podpory; vložka₂ = Rýchlosť v odborníkovi; r₁= Vzdialenosť autora,

r₂= Vzdialenosť od odborníka.

S týmito hodnotami sa získa:

Odpoveď b)

Rovnica, ktorá sa má použiť

v ktorých je možné nahradiť pár hodnôt R a V expertra alebo podporu, pretože v_Do Je to planéta konštanta:

Odpoveď c)

Dĺžka hlavnej poloxle elipsy je Semi -Semi -Semi -Semi -Semi -Seismum a odbornosť:

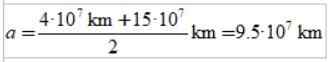
Bibliografia

1. Serway, r., Jewett, J. (2008). Fyzika pre vedu a inžinierstvo. Zväzok 1. Mexiko. Redaktori učenia sa Cengage. 367-372.
2. Stern, D. (2005). Tri Keplerov zákony planétového hnutia. Zdroj z PWG.GSFC.hrniec.Vláda
3. Poznámka: Navrhované cvičenie bolo prijaté a upravené z nasledujúceho textu knihy McGrawhill. Bohužiaľ ide o izolovanú kapitolu vo formáte PDF, bez názvu alebo autor: Mheducation.ES/BCV/Guide/Chapter/844817027X.PDF