Fyzický

Definícia uhlovej rýchlosti, vzorec, výpočet a cvičenia

Definícia uhlovej rýchlosti, vzorec, výpočet a cvičenia

Ten uhlová rýchlosť Je to miera rýchlosti otáčania a je definovaná ako uhol, ktorý otáča polohový vektor objektu, ktorý sa otáča, na jednotku času. Je to veľkosť, ktorá veľmi dobre popisuje pohyb mnohých objektov, ktoré sa neustále otáčajú všade: CD, automobilové kolesá, stroje, zem a mnoho ďalších.

Na nasledujúcom obrázku je možné vidieť schému „London Eye“. Predstavuje pohyb cestujúceho predstavovaného bodom P, ktorý sleduje kruhovú trajektóriu nazývaný C:

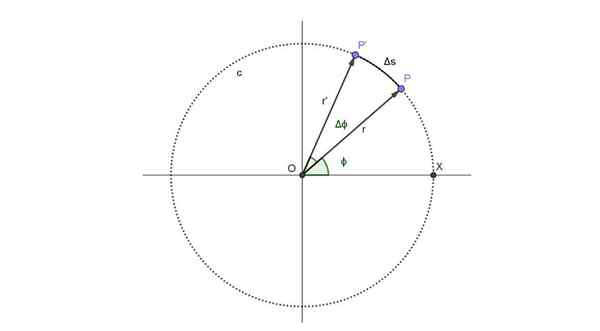Schematické znázornenie obežnej trajektórie, ktorá sleduje cestujúcich „London Eye“. Zdroj: Self Made.

Cestujúci zaberá polohu P v okamihu T a uhlová poloha zodpovedajúca tomuto okamihu je ϕ.

Od okamihu, keď uplynie časové obdobie Δt. V tomto období je nová poloha presného cestujúceho p 'a uhlová poloha zvýšila uhol Δϕ.

[TOC]

Ako sa vypočítava uhlová rýchlosť ?

Pre rotačné veľkosti sa široko používajú grécke písmená, aby sa odlíšili od lineárnych veľkostí. Takže spočiatku je definovaná priemerná uhlová rýchlosť Ωm Keď uhol cestoval v danom časovom období.

Potom kvocient ϕ/δt bude predstavovať priemernú uhlovú rýchlosť Ωm Medzi momentmi t a t+Δt.

Ak chcete vypočítať uhlová rýchlosť Práve v čase t sa potom musí kvocient δ8/δt vypočítať, keď ΔT ➡0:

 Jednotka miery uhlovej rýchlosti je rad/s.

Vzťah medzi lineárnou a uhlovou rýchlosťou

Lineárna rýchlosť vložka, Je to kvocient medzi cestovanou vzdialenosťou a časovým obdobím, ktoré sa používa na jeho cestovanie.

Na obrázku vyššie je trasa oblúka δs. Ale tento oblúk je úmerný prejdenému uhlu a polomeru, ktorý spĺňa nasledujúci vzťah, ktorý je platný, pokiaľ sa meria Δϕ v radiánoch:

Môže vám slúžiť: Metóda rovnobežníka: príklady, vyriešené cvičenia

ΔS = R ・ ϕ

Ak rozdelíme predchádzajúci výraz medzi časové obdobie ΔT a zaujme limit pri ΔT ➡0, dostaneme:

v = r ・ Ω

Jednotný pohyb rotácie

Fotografia je slávny „London Eye“, 135 m vysoké otáčajúce koleso, ktoré sa pomaly otáča, aby ľudia mohli nastúpiť na kabínu na svojej základni a vychutnať si londýnsku krajinu. Zdroj: Pixabay.

Pohyb rotácie je rovnomerný, ak je kedykoľvek pozorovaný, uhol je rovnaký v rovnakom časovom období.

Ak je rotácia rovnomerná, potom sa uhlová rýchlosť kedykoľvek zhoduje s priemernou uhlovou rýchlosťou.

V rovnomernom rotácii v čase, keď sa kompletný zákrut nazýva obdobie a označuje s t.

Okrem toho, keď je uhol otočený, je 2π (ekvivalent k 360 °). Preto v rovnomernej rotácii je uhlová rýchlosť Ω spojená s periódou T pomocou nasledujúceho vzorca:

Frekvencia je definovaná F jednotnej rotácie, ako je kvocient medzi počtom zákrut a časom stráveným pri ich cestovaní. Ako 1 návrat to cestuje v čase t (obdobie) má nasledujúci vzťah:

F = 1/t

Inými slovami, v rovnomernej rotácii je uhlová rýchlosť spojená s frekvenciou podľa:

Ω = 2π ・ f

Vyriešené cvičenia s uhlovou rýchlosťou

Cvičenie 1

Kabíny veľkého rotujúceho kolesa známe ako “Londýnske oko„Pohybujú sa pomaly. Rýchlosť kabín je 26 cm/s a koleso má priemer 135 m.

Pri týchto údajoch vypočítajte:

Môže ti slúžiť: slnko

i) uhlová rýchlosť kolesa

ii) Frekvencia rotácie

iii) Čas, ktorý sa otočí v kabíne.

Odpovede:

Jo) Rýchlosť V v m/s je: v = 26 cm/s = 0,26 m/s.

Rádio je polovica priemeru: r = (135 m) / 2 = 67,5 m

v = r ・ Ω => Ω = v/r = (0,26 m/s)/(67,5 m) = 0,00385 rad/s

Ii) Ω = 2π ・ f => f = Ω / 2π = (0,00385 rad / s) / (2π rad) = 6,13 x 10-4 zákruty

F = 6,13 x 10^-4 otočte.

Iii) T = 1 / f = 1/21 otáčanie / hodinu = 0,45311 čas = 27 min 11 s

Cvičenie 2

Hračkárska auto sa pohybuje na kruhovej dráhe polomeru 2 m. Pri 0 s je jeho uhlová poloha 0 rad, ale po čase je jeho uhlová poloha daná:

φ (t) = 2 ・ t 

Určiť:

i) uhlová rýchlosť 

ii) lineárna rýchlosť kedykoľvek.

Odpovede:

Jo) Uhlová rýchlosť je derivát uhlovej polohy: Ω = φ '(t) = 2.

Inými slovami.

Ii) Lineárna rýchlosť vozidla je: v = r ・ Ω = 2 m ・ 2 rad/s = 4 m/s = 14,4 km/h

Cvičenie 3

Rovnaké auto predchádzajúceho cvičenia sa začína zastaviť. Jeho uhlová poloha ako funkcia času je daná nasledujúcim výrazom:

φ (t) = 2 ・ t - 0,5 ・ t2 

Určiť:

i) uhlová rýchlosť kedykoľvek

ii) lineárna rýchlosť kedykoľvek

iii) Čas, ktorý potrebujete na zastavenie od okamihu, keď začnete spomaľovať

iv) uhol cestoval 

v) na vzdialenosti prešla

Odpovede:

Jo) Uhlová rýchlosť je derivát uhlovej polohy: Ω = φ '(t)

Ω (t) = φ '(t) = (2 ・ t - 0,5 ・ t2) '= 2 - t

Ii) Lineárna rýchlosť vozidla kedykoľvek je daná:

v (t) = r ・ Ω (t) = 2 ・ (2 - t) = 4 - 2 t

Môže vám slúžiť: relatívna rýchlosť: koncept, príklady, cvičenia

Iii) Čas, ktorý preberá okamih, keď sa začína spomaľovať.

v (t) = 4 - 2 t = 0 => t = 2

To znamená, že sa zastaví 2 s po začatí zastavenia.

Iv) V období 2 s, od času, keď sa začne zastaviť, až kým sa prevezme uhol daný φ (2):

φ (2) = 2 ・ 2 - 0,5 ・ 2^2 = 4 - 2 = 2 rad = 2 x 180 / π = 114,6 stupňov

V) V rozpätí 2 s chápaných, pretože sa začne zastaviť, až kým nezastaví vzdialenosť daná:

S = r ・ φ = 2m ・ 2 rad = 4 m

Cvičenie 4

Kolesá automobilu majú priemer 80 cm. Ak sa auto pohybuje rýchlosťou 100 km/h. Nájdite: i) uhlová rýchlosť rotácie kolesa, ii) frekvencia rotácie kolies, iii) počet kôl, ktoré koleso dáva na 1 hodinovej trase.

Odpovede:

Jo) V prvom rade otočíme rýchlosť auta km/h a m/s

V = 100 km / h = (100/3.6) m/s = 27,78 m/s

Uhlová rýchlosť rotácie kolies je daná:

Ω = v/r = (27,78 m/s)/(0,4 m) = 69,44 rad/s

Ii) Frekvencia otáčania kolies je daná:

F = Ω / 2π = (69,44 rad / s) / (2π rad) = 11,05 otáčania / s

Frekvencia rotácie sa zvyčajne vyjadruje v otáčaniach za minútu r.p.m.

F = 11,05 Turn/s = 11,05 Turn/(1/60) min = 663,15 r.p.m

Iii)  Počet zákrut, ktoré koleso dáva na 1 hodinovú trasu, sa vypočíta s vedomím, že 1 hodinu = 60 minút a že frekvencia je počet zákrut n vydelený časom, v ktorom sú tieto n.

F = n / t => n = f ・ t = 663,15 (zákruty / min) x 60 min = 39788,7 zákruty.

Odkazy

  1. Giancoli, D. Fyzika. Zásady s aplikáciami. 6. vydanie. Sála. 106-108.
  2. Resnick, r. (1999). Fyzický. Zväzok 1. Tretie vydanie v španielčine. Mexiko. Kontinentálna redakčná spoločnosť s.Do. c.Vložka. 67-69.
  3. Serway, r., Jewett, J. (2008). Fyzika pre vedu a inžinierstvo. Zväzok 1. 7. Vydanie. Mexiko. Redaktori učenia sa Cengage. 84-85.
  4. Geogebra.orgán