Charakteristické vektory jednotiek, ako to dostať von, príklady

Ten vektory sú tí, ktorých modul, veľkosť alebo veľkosť sa rovná numerickej hodnote One. Jednotkové vektory sú užitočné na označenie smeru iných vektorov, ktoré nie sú unitované.

Pripomeňme, že vektory sú matematické entity, ktoré matematicky predstavujú fyzikálne veľkosti, ktoré závisia od smeru, ako je sila, rýchlosť, zrýchlenie a ďalšie.

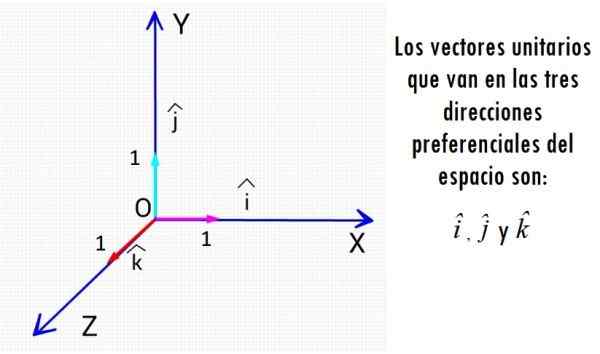
Najznámejšie jednotkové vektory sú tri vektory, ktoré idú v smere karteziánskych osí. Zdroj: f. Zapata.

Bez ohľadu na fyzickú veľkosť, ktorá je spojená, jednotkové vektory sú entitami, ktoré chýbajú jednotky merania a ich veľkosť je vždy 1, čisté číslo.

Napríklad rýchlosť častice, ktorá sa pohybuje pri 3 m/s a ide v pozitívnom smere osi karteziánskej x, je označená:: vložka = (3 m/s) Jo, kde sa výrazné písmeno používa na označenie sumy vektora. V tomto príklade modul vložka Je 3 m/s a modul jednotkového vektora Jo je 1 (bez jednotiek).

[TOC]

Modul, smer a význam

Vzhľadom na dôležité. V čase reprezentácie vektora je potrebné tieto aspekty jasne uviesť.

Teraz môže mať jednotkový vektor akýkoľvek smer a význam, ktorý je preferovaný, ale veľkosť sa musí vždy rovnať 1.

Jednotkové vektory sa používajú na označenie súkromnej adresy vo vesmíre alebo v lietadle. Ak napríklad musíme pracovať so všetkými silami, ktoré pôsobia pozdĺž vodorovnej osi, pretože jednotkový vektor v tomto smere nám pomáha rozlíšiť tieto sily od ostatných smerovaných iným smerom.

A aby sa ich odlíšili od vektorov, ktoré nie sú unitmi, tučný tučný stav sa zvyčajne používa v tlači a umiestni napríklad obvodový prízvuk na vrchol:

Môže vám slúžiť: Stacionárna teória štátu: História, vysvetlenie, správy

Pre ručne písané texty stačí umiestniť obirflejo, aby sme pochopili, že ide o jednotkový vektor.

Charakteristiky jednotkového vektora

Matematicky vektor jednotky:

Je to prvok, ktorý patrí do vektorového priestoru ℛ dimenzie n, takže |vložka| = 1, kde pruhy znamenajú „modul“.

Takže to môžeme zistiť:

-Jednotný vektorový modul je vždy 1, nezáleží na tom, či ide o pevnosť, rýchlosť alebo iný vektor.

-Jednotkové vektory majú určitý smer, ako aj smer, ako napríklad jednotkový vektor vo vertikálnom smere, ktorý môže mať zmysel hore alebo dole.

-Jednotkové vektory majú bod pôvodu. Ak je predstavený karteziánskym súradnicovým systémom, uvedený bod sa zhoduje s pôvodom systému: (0,0) Ak je to rovina alebo (0,0,0), ak je vektor v trojrozmernom priestore.

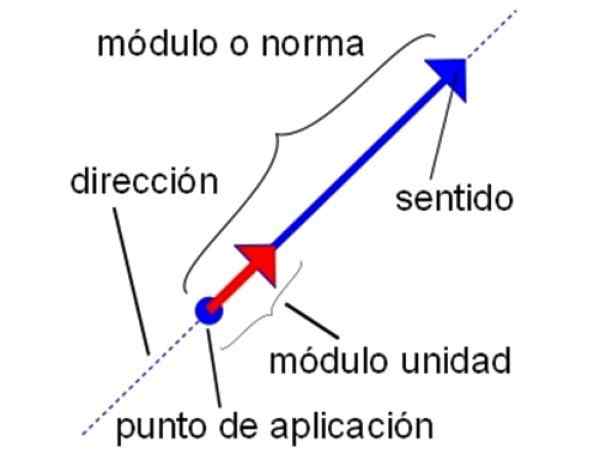Charakteristiky vektora jednotky. Zdroj: Wikimedia Commons.

-Tiež s jednotkovými vektormi je možné vykonať všetky operácie súčtu, odčítania a násobenia vektorov, ktoré sú vyrobené bežnými vektormi. Preto je platné vynásobiť jednotkový vektor skalárnym, ako aj vykonať bodový produkt a krížový produkt.

-S jednotkovým vektorom v určitom smere je možné vyjadriť aj iné vektory, ktoré sú tiež orientované v tomto smere.

Jednotkové vektory vo vesmíre

Na vyjadrenie akéhokoľvek vektora vo vesmíre alebo v rovine môžete použiť sadu jednotných vektorov kolmých na seba, ktoré tvoria ortonormálnu základňu. Každý z troch preferenčných smerov priestoru má svoj vlastný jednotkový vektor.

Vráťme sa k príkladu síl nasmerovaných pozdĺž horizontálnej osi. Toto je os x, ktorá má dve možnosti: smer doprava a smer doľava. Predpokladajme, že na osi X je vektor jednotky a nasmerovaný doprava, ktorý môžeme označiť v ktorejkoľvek z týchto foriem:

Môže vám slúžiť: Thomson Atomic Model: Charakteristiky, postuláty, subatomické častice

Ktorýkoľvek z nich je platný. Teraz predpokladajme silu F₁ veľkosti 5 n pozdĺž tejto osi a nasmerované doprava, takáto sila by sa mohla vyjadriť ako:

Keby bola sila nasmerovaná pozdĺž osi x, ale v opačnom smere, to znamená vľavo, potom by sa na stanovenie tohto rozdielu mohla použiť negatívny znak.

Napríklad, 8 N sila veľkosti, umiestnená na osi X a nasmerovaná doľava by bola takáto:

Alebo tak:

A pre vektory, ktoré nie sú namierené pozdĺž karteziánskych osí, existuje aj spôsob, ako ich reprezentovať, pokiaľ ide o ortogonálne vektory jednotiek prostredníctvom svojich karteziánskych komponentov.

Ako odstrániť/vypočítať vektor jednotky?

Na výpočet vektora jednotky v smere ľubovoľného ľubovoľného vektora vložka, Použije sa nasledujúci vzorec:

Kde:

Je to modul alebo veľkosť vektora vložka, ktorého štvorec sa počíta takto:

|vložka|² = (v_X)² +  (v_a)²+  (vložka_z)²

Ľubovoľný vektor z hľadiska jednotkového vektora

Alternatívne vektor vložka Môže sa vyjadriť takto:

To znamená produkt jeho modulu zodpovedajúcim jednotkovým vektorom. To je presne to, čo sa stalo predtým, keď hovoril o sile 5 n veľkosti nasmerovanej pozdĺž kladnej osi x.

Grafická reprezentácia

Graficky to, čo sa hovorí, je vidieť na tomto obrázku, kde vektor vložka Je v modrej farbe a zodpovedajúci vektor jednotky v jeho smere je červený.

V tomto príklade vektor vložka Má veľkosť väčšie ako veľkosť jednotkového vektora, ale vysvetlenie je dokonca platné, ak sa tak nestane. Inými slovami, môžeme mať vektory, ktoré sú napríklad 0.25 -násobok vektora jednotky.

Môže vám slúžiť: hmotnosť (fyzická): výpočet, jednotky, príklady, cvičenia

Príklady jednotkových vektorov

Kolmé vektory jednotiek I, J a K

Ako sme videli predtým, kolmé vektory jednotiek Jo, J a klimatizovať Sú veľmi užitočné na reprezentáciu akéhokoľvek iného vektora v lietadle alebo priestore a vykonávajú vektorové operácie. Pokiaľ ide o uvedený vektor, je ľubovoľný vektor V reprezentovaný ako:

vložka = v_X Jo + vložka_a J + vložka_z klimatizovať

Kde v_X, vložka_a a v_z sú obdĺžnikové komponenty vektora vložka, ktoré sú výstupy-.

Coulombov zákon

Unitárne vektory sa často objavujú vo fyzike. Tam máme napríklad Coulombov zákon, ktorý kvantitatívne opisuje interakciu medzi dvoma konkrétnymi elektrickými nábojmi.

To naznačuje, že sila F príťažlivosti alebo odporu medzi týmito zaťaženiami je úmerná ich produktu, nepriamo úmerne k štvorcovi vzdialenosti, ktorá ich oddeľuje a je nasmerovaná v smere vektora jednotky, ktorý spája zaťaženie.

Tento vektor je zvyčajne reprezentovaný:

A Coulombov zákon je taký, vo vektorovej podobe:

Kde klimatizovať Je to elektrostatická konštanta, Otázka₁ a Otázka₂ Sú to záťaže a r Je to vzdialenosť, ktorá ich oddeľuje.

Cvičenie

Nájdite vektor jednotky v smere vektora vložka = 5Jo + 4J -8klimatizovať, Uvedené v ľubovoľných jednotkách.

Riešenie

Vymedzenie vyššie uvedeného definície jednotného vektora je uvedené vyššie:

Najprv však musíte vypočítať vektorový modul, ktorý má tri komponenty, je určený:

|vložka|² = (v_X)² +  (v_a)² +  (v_z)²

Zostať:

|vložka|² = (5)² +  (4)² +  (-8)²= 25 + 16 + 64 = 105

Preto modul vložka je:

|vložka| = √105

Vyhľadaný jednotný vektor je jednoducho:

To nás nakoniec vedie k:

vložka = 0.488 Jo + 0.390 J - 0.781 klimatizovať

Odkazy

1. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill.
2. Bedford, 2000. Do. Mechanika pre inžinierstvo: statické. Addison Wesley.
3. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 1. Kinematika. Editoval Douglas Figueroa (USB).
4. Giambattista, a. 2010. Fyzika. Druhý. Edimatizovať. McGraw Hill.
5. Resnick, r. (1999). Fyzický. Zvuk. 1. 3. vydanie. v španielčine. Kontinentálna redakčná spoločnosť s.Do. c.Vložka.