Úmerná variácia

Čo je proporcionálna variácia?

Proporcionálna variácia medzi dvoma premennými „x“ a „y“ dochádza k vynásobeniu jednej z nich jednou konštantou, druhá je tiež vynásobená alebo vydelená rovnakou konštantou. Mnoho situácií skutočného sveta s nimi možno správne opísať.

Proporcionalita medzi premennými môže byť priama alebo inverzná. V priamej proporcionalite je vzťah typu:

y = k ∙ x

Alebo ekvivalentne:

K = y/x

Kde k je konštanta volá primeranosť ani pomer proporcionality. Všimnite si, že ak sa „x“ zvýši, „y“ to urobí v rovnakom pomere a ak „x“ klesne, bude tiež „y“. Keď je vzťah medzi premennými grafy, získa sa priama čiara, ktorá prechádza pôvodom súradníckeho systému (pozri cvičenie vyriešené neskôr).

Priama variácia sa môže vyskytnúť aj medzi jednou premennou a jednou silou druhej, napríklad „y“ môže byť priamo úmerná x², X³ a tak.

Na druhej strane, v opačnej proporcionalite sú premenné spojené výrazom:

x ∙ y = k

Tento výraz znamená, že produkt premenných je konštanta. Pri grafe vzťahu medzi premennými je hyperbola. Tiež, ak je produkt premennej s jednou silou druhej konštantný, predstavuje tiež prípad spätnej proporcionality, napríklad:

X²∙ y = k; X³∙ y = k ..

Príklady

Aplikácia proporcionálnych variácií je rozloženie máp

Mnoho zákonov fyziky a chémie sa vyjadruje matematicky ako rozmery. Napríklad sila, ktorá uplatňuje pružinu a predĺženie,, vzťah medzi tlakom a objemom v plyne pri konštantnej teplote, perióda jednoduchého kyvadla a druhej druhej korene jeho dĺžky a mnoho ďalších. Poznanie modelu, ktorý riadi tento jav, môžete zistiť svoje správanie pre akúkoľvek hodnotu premenných.

Môže vám slúžiť: Existencia a jedinečnosť veta: demonštrácia, príklady a cvičenia

A nielen to, že sa uplatňujú aj v nespočetných situáciách, ako sú tieto:

• Odovzdajte vzor odevu menšej veľkosti na väčšiu veľkosť (alebo naopak).
• V konverzných faktoroch sa presunúť z jednej jednotky na druhú, ako sú kilometre na míle, galóny do litrov a ďalšie.
• Vypočítajte ingrediencie receptu pre 6 ľudí, ktorí poznajú požiadavku 4 ľudí.
• Určiť sumu určitých daní v súlade so získaným príjmom.
• Pri výpočte jednoduchého záujmu.
• Pri kreslení lietadiel na stupnici.
• Ak musíte vypočítať cenu množstva výrobkov, ktorí poznajú jednotkovú cenu.
• V podobnosti trojuholníkov.

Ďalej, podrobne, existujú dve zaujímavé situácie, v ktorých sa uplatňujú proporčné variácie:

Príklad 1

Na stupnici mesta merala Hermitage Avenue 3.2 cm, čo je skutočná dĺžka 400 m. Na druhej strane, ulica La Fuente, ktorá skutočne meria 180 me. Aká je veľkosť mŕtvice?

Vyhlásenie ponúka úplné informácie o ulici Ermita: Nech je skutočná dĺžka cesty a ℓ jej dĺžka v rovine, pretože variácia je priamej proporcionality, musí:

L = k ∙ ℓ

Z údajov na Hermitage Avenue môžete poznať hodnotu proporcionality konštanty k, ale predtým, ako je potrebné nechať všetky dĺžky v rovnakých jednotkách:

3.2 cm = 0.032 m

Tak:

400 m = k ∙ 0.032 m

Preto konštanta proporcionality je:

Môže vám slúžiť: Aké sú prvky podobenstva? (Časti)

K = 400 /0.032 = 12500

Teraz je známe, že:

L = 12500 ∙ ℓ

Tento výsledok sa interpretuje takto: dĺžka ulíc na tejto mape je 12500 -krát menšia ako jej skutočná dĺžka. Preto opatrenia na ulici La Fuente:

ℓ = 180 m/ 12500 = 0.0144 m = 1.44 cm

Príklad 2

Analytik má nasledujúcu tabuľku hodnôt pre premenné „x“ a „y“ získané experimentálne a chce vedieť, či tieto údaje zodpovedajú modelu priamej proporcionálnej variácie alebo jednej z inverznej proporcionálnej variácie.

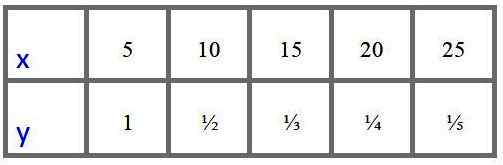
Čo by ste mali vedieť, aby ste to vedeli?

V prvom rade sa zistilo, že keď sa „x“ zvyšuje, „y“ klesá, takže má v každom prípade podozrenie na spätnú proporcionalitu, aby sa zabezpečilo, že analytik má možnosť posúdiť, či je kvocient a/x konštantné (proporcionálne (proporčné priame variácie) alebo ak je produkt x.a je konštantná (inverzná proporcionálna variácia).

Testovanie s prvou možnosťou:

1 ÷ 5 = 0.2

½ ÷ 10 = 0.05

⅓ ÷ 15 = 0.022 ..

Dospelo sa k záveru, že nejde o priamu proporcionálnu variáciu, pretože kvocient a/x poskytujú rôzne hodnoty pre každých pár údajov.

Musíme skontrolovať, či je produkt X ∙ konštantný:

5 × 1 = 5

10 × ½ = 5

15 × ⅓ = 5

20 × ¼ = 5

25 × ⅕ = 5

A ako produkt x ∙ y = 5 sa dospelo k záveru, že variácia je reverznej proporcionality.

Tieto informácie slúžia na poznanie hodnôt, ktoré nie sú v tabuľke, napríklad, aká by bola hodnota „y“, keď x = 30?

Z x ∙ y = 5 sa „y“ vymaže a vymení x = 30:

y = 5/x

y = 5/30 = 1/6

Cvičenie

Ak stojí tkanina meter.75 dolárov a s vedomím, že cena je priamo úmerná množstvu metrov na nákup, nájdite:

Môže vám slúžiť: Antidevatívne: vzorce a rovnice, príklady, cvičenia

a) Algebraický výraz, ktorý spája premenné „Cena za $“ a „počet metrov tkaniny“.

b) Pripravte tabuľku hodnôt s cenami za 3, 6, 9, 12, 15 a 18 metrov tkaniny.

c) graf Získané hodnoty.

Odpovedať

Nechajte „Y“ Cena premennej za $ “a„ X “Variabilné„ množstvo metrov látky “. Ako sú priamo proporcionálne, musíte:

y = k ∙ x

Pre x = 1 meter, y = 6.75 dolárov, preto k = 6.75 $/meter. Toto je jednotková cena látky, cena akejkoľvek inej textílií „X“ sa získa vynásobením tejto hodnoty, potom je požadovaný algebraický výraz:

y = 6.75 ∙ x

Odpoveď B

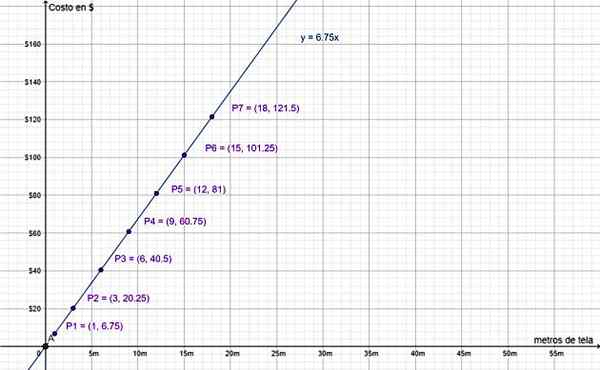
Tabuľka hodnôt s cenami za $ za 3, 6, 9, 12, 15 a 18 metrov je:

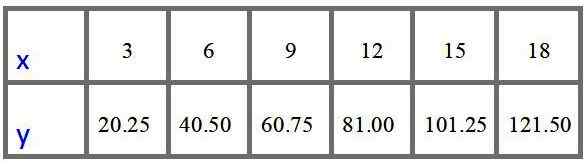
Odpoveď c

Nakoniec graf hodnôt v predchádzajúcej tabuľke potvrdzuje, že ide o priamu proporcionálnu variáciu:

Náklady na $ a množstvo metrov tkaniny sú priamo úmerné sumy. Zdroj: f. Zapata.

Všimnite si, že hodnota (0,0) je zahrnutá, pretože riadok y = 6.75 ∙ x prechádza pôvodom súradníckeho systému, ako je vysvetlené predtým. Dáva to zmysel, pretože nevykonávanie nákupu je rovnocenné s nákupom 0 m látky, ktorej hodnota je 0 $.

Odkazy

1. Larson, R. 2012. Predbežná časť. 8. Vydanie. Učenie sa.
2. Mexické sekretariát verejného vzdelávania. Proporcionálna variácia. Zdroj: PPS.K12.Alebo.my.
3. Stewart, J. 2007. Predklulácia: matematika na výpočet. 5. Vydanie. Učenie sa.
4. Žobrák. Sprievodcovia štúdie: matematika i. Získané z: Dirre.Žobrák.mx.
5. Zill, D. 2008. Predklulácia s výpočtovými pokrokmi. 4. Vydanie. McGraw Hill.