Nepretržité variabilné charakteristiky, príklady a cvičenia

- 2341
- 41
- Denis Škriniar
Ten Kontinuálna premenná Je to jeden, ktorý môže mať nekonečný počet číselných hodnôt medzi dvoma danými hodnotami, aj keď sú tieto dve hodnoty svojvoľne zatvorené. Používajú sa na opis merateľných atribútov; napríklad výška a hmotnosť. Hodnoty prijaté kontinuálnou premennou môžu byť racionálne čísla, reálne čísla alebo zložité čísla, hoci tento posledný prípad je v štatistike menej častý.
Hlavnou charakteristikou kontinuálnych premenných je, že medzi dvoma racionálnymi alebo skutočnými hodnotami sa dajú vždy nájsť a medzi tým ostatnými a prvými môže nájsť inú hodnotu, a tak na neurčito.
 postava 1. Krivka predstavuje nepretržité rozdelenie a tyče diskrétne. Zdroj: Pixabay
postava 1. Krivka predstavuje nepretržité rozdelenie a tyče diskrétne. Zdroj: Pixabay Predpokladajme napríklad premennú hmotnosti v skupine, kde má najväčšia hmotnosť 95 kg a najnižšiu hmotnosť 48 kg; To by bol rozsah premennej a počet možných hodnôt je nekonečný.
Napríklad medzi 50,00 kg a 50,10 kg môže byť 50,01. Ale medzi 50,00 a 50,01 opatrenie môže byť 50 005. To je kontinuálna premenná. Na druhej strane, ak v možných hmotnostných meriach sa vytvorila jedna desatinná presnosť, použitá premenná by bola diskrétna.
Kontinuálne premenné patria do kategórie kvantitatívnych premenných, pretože majú pridruženú číselnú hodnotu. S touto číselnou hodnotou je možné vykonať matematické operácie od aritmetických až po metódy nekonečného výpočtu.
[TOC]
Príklady
Väčšina premenných fyziky sú kontinuálne premenné, medzi nimi môžeme pomenovať: dĺžka, čas, rýchlosť, zrýchlenie, energia, teplota a ďalšie.
Nepretržité premenné a diskrétne premenné
V štatistike je možné definovať rôzne typy premenných, kvalitatívne aj kvantitatívne. Nepretržité premenné patria do tejto poslednej kategórie. S nimi je možné vykonať aritmetické a výpočtové operácie.
Napríklad premenná h, zodpovedá ľuďom s výškou medzi 1,50 m a 1,95 m, je to kontinuálna premenná.
Porovnajme túto premennú s touto inou: počet drahých pri spustení meny, ktorú zavoláme n.
Premenná n Môžete si však vziať hodnoty medzi 0 a nekonečno n Nie je to kontinuálna premenná, pretože nemôže mať hodnotu 1,3 alebo 1,5, pretože medzi hodnotami 1 a 2 nie je žiadny iný. Toto je príklad Diskrétna premenná.
Cvičenie nepretržitých premenných
Zoberme si nasledujúci príklad: Stroj vytvára zhody s fosforom a zabalí ich do svojho boxu. Sú definované dve štatistické premenné:
Môže vám slúžiť: izobarický proces: vzorce, rovnice, experimenty, cvičeniaPremenná 1: l = dĺžka plódy.
Premenná 2: n = počet ošípaných na krabicu.
Dĺžka nominálnych zápasov je 5,0 cm s toleranciou 0,1 cm. Počet ošípaných na krabicu je 50 s toleranciou 3.
a) Uveďte rozsah hodnôt, ktoré môžu trvať L a N.
b) Koľko hodnôt si môžete vziať L?
c) Koľko hodnôt si môžete vziať n?
Povedzte v každom prípade, ak ide o diskrétnu alebo kontinuálnu premennú.
Riešenie
Hodnoty L Sú chápané v intervale [5,0-0,1; 5,0+0,1]; to znamená, že hodnota L je v intervale [4,9 cm; 5.1 cm] a premenná L Medzi týmito dvoma opatreniami môžete brať nekonečné hodnoty. Je to potom kontinuálna premenná.
Hodnota premennej n je v intervale [47; 53]. Premenná n Môže trvať iba 6 možných hodnôt v intervale tolerancie, potom je to diskrétna premenná.
Cvičenie rozdelenia pravdepodobnosti
Ak je okrem kontinuálneho, hodnoty prijaté premennou spojené s určitou pravdepodobnosťou výskytu, potom je to Nepretržitá náhodná premenná. Je veľmi dôležité rozlíšiť, či je premenná diskrétna alebo kontinuálna, pretože pravdepodobnostné modely použiteľné navzájom sa líšia.
Kontinuálna náhodná premenná je úplne definovaná, keď sú známe hodnoty, ktoré môžu predpokladať, a pravdepodobnosť, že každý z nich musí dôjsť.
-Cvičenie 1 pravdepodobností
Zodpovedá továreň ich robí takým spôsobom, že dĺžka paličiek je vždy medzi hodnotami 4,9 cm a 5,1 cm a nula z týchto hodnôt. Existuje pravdepodobnosť získania tyčinky, ktorá meria medzi 5,00 a 5,05 cm, hoci by sme mohli tiež extrahovať jedného z 5.000 cm. Sú tieto hodnoty rovnako pravdepodobné?.
Môže vám slúžiť: relatívna hustota: výpočet, príklady, cvičeniaRiešenie
Predpokladajme, že hustota pravdepodobnosti je jednotná. Ďalej je uvedená šanca na nájdenie fosforu s určitou dĺžkou:
-Že fosfor je v rozsahu [4,9; 5,1] má pravdepodobnosť = 1 (alebo 100%), pretože stroj z týchto hodnôt nezbavuje zhody.
-Nájdenie fosforu, ktorý je medzi 4,9 a 5,0, má pravdepodobnosť = ½ = 0,5 (50%), pretože je to polovica rozsahu dĺžok.
-A pravdepodobnosť, že zhoda má dĺžku medzi 5,0 a 5,1, je tiež 0,5 (50%)
-Je známe, že neexistujú žiadne tyčinky fosforu, ktoré majú dĺžku medzi 5,0 a 5,2. Pravdepodobnosť: nula (0%).
Pravdepodobnosť nájsť palicu v určitom rozsahu
Teraz si uvedomme nasledujúce pravdepodobnosti, aby ste získali palice, ktorých dĺžka je medzi L1 a l2:
P = (l2 -l1) /(LMaximálny - Lblesk)
-P, že zhoda má dĺžku medzi 5,00 a 5,05, je označená ako P ([5,00; 5,05]):
P ([5,00; 5,05]) = (5,05 - 5,00)/(5,1 - 4,9) = 0,05/0,2 = ¼ = 0,25 (25%)
-P, že Cerrillo má dĺžku medzi 5,00 a 5,01, je:
P ([5,00; 5,01]) = (5,00 - 5,01)/(5,1 - 4,9) = 0,01/0,2 = 1/20 = 0,05 (5 %)
-P that the cerrillo has length between 5,000 and 5,001 is even lower:
P (5 000; 5 001) = 0,001/0,2 = 1/200 = 0,005 (0,5%)
Ak budeme naďalej znižovať interval, aby sme sa čoraz viac a viac priblížili k 5,00, pravdepodobnosť, že palica má presne 5,00 cm, je nula (0%). Čo máme, je pravdepodobnosť nájsť zhodu v určitom rozsahu.
Pravdepodobnosť nájsť niekoľko paličiek v určitom rozsahu
Ak sú udalosti nezávislé, pravdepodobnosť, že dve palice sú v určitom rozsahu, je produktom ich pravdepodobností.
-Pravdepodobnosť, že dve palice sú medzi 5,0 a 5,1, je 0,5*0,5 = 0,25 (0,25%)
-Pravdepodobnosť, že 50 paličiek je medzi 5,0 a 5,1, je (0,5)^50 = 9 × 10^-16, to je takmer nulové.
-Pravdepodobnosť, že 50 tyčiniek je medzi 4,9 a 5,1, je (1)^50 = 1 (100%)
-Cvičenie 2 pravdepodobností
V predchádzajúcom príklade sa predpokladalo, že pravdepodobnosť je v danom intervale rovnomerná, ale nie vždy tomu tak.
Môže vám slúžiť: hydrostatický tlak: vzorec, výpočet, príklady, cvičeniaV prípade skutočného stroja, ktorý produkuje palice, je možnosť, že palica je v centrálnej hodnote, je väčšia ako v jednej z extrémnych hodnôt. Z matematického hľadiska je to modelované pomocou funkcie F (x) známe ako hustota pravdepodobnosti.
Pravdepodobnosť, že miera je medzi A a B, sa vypočíta pomocou definovaného integrálu funkcie f (x) medzi A a B.
Predpokladajme, že chceme nájsť funkciu F (x), ktorá predstavuje rovnomerné rozdelenie medzi hodnotami 4,9 a 5,1 cvičenia 1.
Ak je rozdelenie pravdepodobnosti rovnomerné, potom sa F (x) rovná konštantnej C, ktorá je určená, že bude mať integrál medzi 4,9 a 5,1 C. Pretože tento integrál je pravdepodobnosť, takže výsledkom musí byť 1.
 Obrázok 2. Rovnomerná hustota pravdepodobnosti. (Vlastné rozpracovanie)
Obrázok 2. Rovnomerná hustota pravdepodobnosti. (Vlastné rozpracovanie) Čo znamená, že C má hodnotu 1/0,2 = 5. Inými slovami, rovnomerná funkcia hustoty pravdepodobnosti je F (x) = 5, ak 4,9 Poznámka ako v intervaloch rovnakej šírky (napríklad 0,02) Pravdepodobnosť je rovnaká v strede ako na konci kontinuálneho rozsahu premenných L (Dĺžka uhorky). Realistickejším modelom by bola funkcia hustoty pravdepodobnosti, ako je toto: -f (x) = -750 ((x-5,0)^2-0,01), ak 4,9 -0 mimo tohto rozsahu Na obrázku 3 je možné pozorovať, že je pravdepodobnosť nájdenia tyčiniek medzi 4,99 a 5,01 (šírka 0,02) väčšia ako nájdenie tyčiniek medzi 4,90 a 4,92 (šírka 0,02)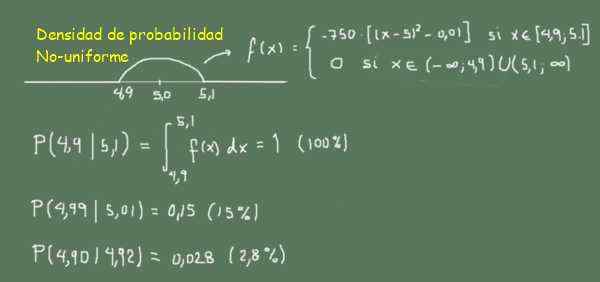 Obrázok 3. NEUSUNIformná funkcia hustoty pravdepodobnosti. (Vlastné rozpracovanie)
Obrázok 3. NEUSUNIformná funkcia hustoty pravdepodobnosti. (Vlastné rozpracovanie) Odkazy
- « Trvalo udržateľný pôvod architektúry, princípy, aplikácie, materiály
- Termodynamické premenné, ktoré sú a vyriešené cvičenia »

