História trojuholníkov, prvky, klasifikácia, vlastnosti

Ten trojuholníky Sú to ploché a uzavreté geometrické postavy, ktoré pozostávajú z troch strán. Trojuholník je určený tromi čiarami, ktoré sú rezané dva až dva a navzájom sa tvoria tri uhly. Trojuholníková forma plná symboliky je prítomná v nespočetných objektoch a ako prvok konštrukcie.

Pôvod trojuholníka sa stratí v histórii. Z archeologických dôkazov je známe, že primitívne ľudstvo ho poznalo dobre, pretože archeologické zvyšky potvrdzujú, že bol použitý v nástrojoch a zbraniach.

postava 1. Trojuholníky. Zdroj: verejné domény.

Je tiež zrejmé, že starí Egypťania mali solídne vedomosti o geometrii a najmä o trojuholníkovej podobe. Boli stelesnení v architektonických prvkoch svojich monumentálnych konštrukcií.

V Rhind Papyrus sú vzorce na výpočet trojuholníkov a lichobežníkov, ako aj niektoré zväzky a ďalšie koncepty základnej trigonometrie.

Na druhej strane je známe, že Babylončania boli schopní vypočítať oblasť trojuholníka a ďalšie geometrické postavy, ktoré použili na praktické účely, ako napríklad rozdiely v krajine. Tiež si boli vedomí mnohých vlastností trojuholníkov.

Boli to však starí Gréci, ktorí dnes systematizovali mnohé časté geometrické koncepty, hoci veľká časť týchto vedomostí nebola výlučná, pretože sa určite zdieľala s týmito ďalšími starodávnymi civilizáciami.

[TOC]

Prvky trojuholníka

Prvky akéhokoľvek trojuholníka sú uvedené na nasledujúcom obrázku. Existujú tri: vrcholy, boky a uhly.

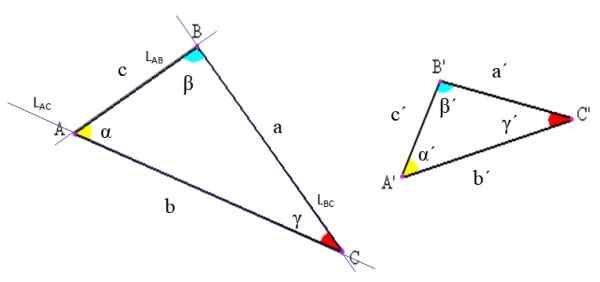Obrázok 2. Notácia trojuholníkov a ich prvkov. Zdroj: Wikimedia Commons, upravené f. Zapata

-Vrcholy: Toto sú križovatky liniek, ktorých segmenty určujú trojuholník. Napríklad na hornom obrázku čiara L_Ac ktorý obsahuje segment striedavého prúdu, pretína čiaru L_AB ktorý obsahuje segment AB práve v bode a.

-Strany: Medzi každým niekoľkým vrcholom je nakreslený segment čiary, ktorý predstavuje jednu stranu trojuholníka. Tento segment je možné označiť písmenami koncov alebo pomocou konkrétneho listu, aby ste ho nazvali. V príklade na obrázku 2 sa strana AB nazýva tiež „C“.

-Uhly: Medzi každou stranou so spoločným vrcholom je uhol, ktorého vrchol sa zhoduje s výškou trojuholníka. Uhol sa všeobecne označuje gréckym listom, ako je uvedené na začiatku.

Ak chcete zostaviť konkrétny trojuholník, s daným tvarom a veľkosťou, majú iba niektoré z nasledujúcich súborov údajov:

-Tri strany, celkom zrejmé v prípade trojuholníka.

-Dve strany a uhol medzi nimi a zostávajúca strana sa okamžite nakreslí.

-Dva uhly (vnútorné) a strana medzi nimi. Predĺženia sú nakreslené dve chýbajúce strany a trojuholník je pripravený.

Notácia

Všeobecne sa v zápise trojuholníkov používajú nasledujúce konvencie: vrcholy sú označené kapitálovými písmenami, bokmi s malými latinskými písmenami a uhlami gréckymi písmenami (pozri obrázok 2).

Týmto spôsobom je trojuholník pomenovaný podľa jeho vrcholov. Napríklad trojuholník vľavo na obrázku 2 je trojuholník ABC a ten vpravo je trojuholník a'b'c '.

Je tiež možné použiť iné zápisy; Napríklad uhol a na obrázku 2 je označený ako BAC. Všimnite si, že písmeno vrcholu ide do stredu a písmená sú napísané opačným smerom ako ihly s hodinami.

Môže vám slúžiť: vymedzenie problému

Inokedy je kladený prízvuk obvodu, ktorý označuje uhol:

Alebo sa používa symbol ∠, pretože predchádzajúci zápis nemusí byť v tlači ľahký, po ktorom nasleduje písmeno zodpovedajúce vrcholu:

α = ∠A

Typy trojuholníkov

Existuje niekoľko kritérií klasifikácie trojuholníkov. Najbežnejšie je ich klasifikovať podľa miery ich strán alebo podľa miery ich uhlov. V závislosti od miery ich strán môžu byť trojuholníky: Scalenes, Isosceles alebo Equilaterals:

-Vyskakovať: Jeho tri strany sú rôzne.

-Izoscely: Má dve rôzne strany a jedna.

-Rovnocenný: Tri strany sú rovnaké.

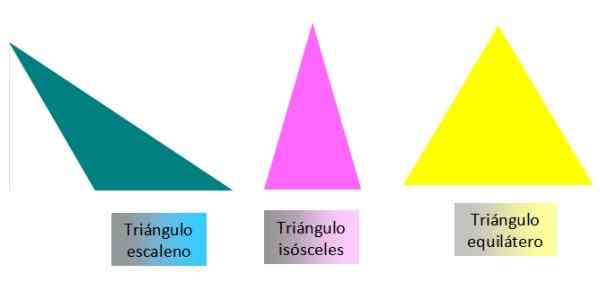Obrázok 3. Klasifikácia trojuholníkov na ich stranách. Zdroj: f. Zapata

Podľa miery ich uhlov sa trojuholníky nazývajú takto:

-Tupý, Ak je jeden z vnútorných uhlov väčší ako 90 °.

-Akulógový, Keď sú tri vnútorné uhly trojuholníka akútne, to znamená menej ako 90 °

-Obdĺžnik, V prípade, že jeden z jeho vnútorných uhlov má hodnotu 90 °. Strany, ktoré tvoria 90 °, sa nazývajú katetos a opačná strana k pravému uhlu je hypotenus.

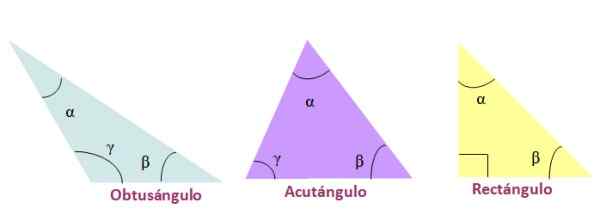Obrázok 4. Klasifikácia trojuholníkov podľa ich vnútorných uhlov. Zdroj: f. Zapata.

Zhoda trojuholníkov

Keď majú dva trojuholníky rovnaký tvar a majú rovnakú veľkosť, hovorí sa, že sú zhodní. Kongruencia samozrejme súvisí s rovnosťou, tak prečo v geometrii hovoríme o „dvoch zhodných trojuholníkoch“ namiesto „dvoch rovnakých trojuholníkov“?

Uprednostňuje sa, že pojem „kongruencia“ sa drží pravdy, pretože dva trojuholníky môžu mať rovnaký tvar a veľkosť, ale v rovine sa orientovať inak (pozri obrázok 3). Z hľadiska geometrie by už neboli prísne rovnaké.

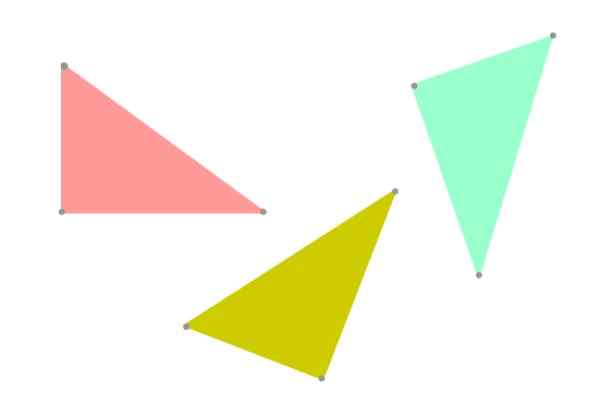Obrázok 5. Zhodné trojuholníky, ale nie nevyhnutne to isté, pretože jej orientácia v lietadle je iná. Zdroj: f. Zapata.

Zhodné kritériá

Dva trojuholníky sú zhodné, ak dôjde k niektorým z nasledujúcich situácií:

-Tri strany merajú rovnako (opäť je to najzreteľnejšie).

-Majú dve rovnaké strany a s rovnakým uhlom medzi nimi.

-Obidva majú dva rovnaké vnútorné uhly a strana medzi týmito uhlami je rovnaká.

Ako je vidieť, ide o dva trojuholníky spĺňajú potrebné podmienky, takže pri ich stavbe sú ich tvar a veľkosť presne rovnaké.

Kritériá zhody sú veľmi užitočné, pretože v praxi sa v praxi musia v sérii vyrábať nespočetné množstvo mechanických častí a častí, takže ich opatrenia a forma sú presne rovnaké.

Podobnosť trojuholníkov

Trojuholník je podobný inému, ak majú rovnaký tvar, aj keď majú inú veľkosť. Aby sa zabezpečilo, že tvar je rovnaký, je potrebné, aby vnútorné uhly mali rovnakú hodnotu a že strany sú proporcionálne.

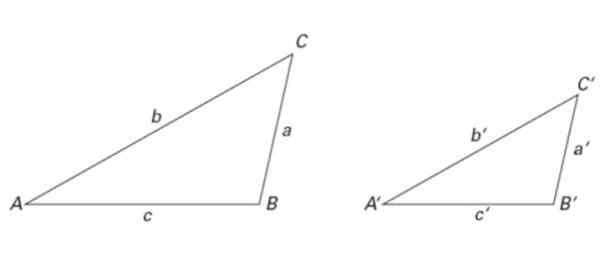Obrázok 6. Dva podobné trojuholníky: ich veľkosti sa líšia, ale ich rozmery sú rovnaké. Zdroj: f. Zapata.

Trojuholníky na obrázku 2 sú tiež podobné, ako aj na obrázku 6. Teda:

∠ A = ∠ A ', ∠ B = ∠ B 'a ∠ C = ∠ C '

Pokiaľ ide o strany, sú splnené nasledujúce dôvody podobnosti:

a/a '= b/b' = c/c '

Vlastnosti

Základné vlastnosti trojuholníkov sú nasledujúce:

-Súčet vnútorných uhlov akéhokoľvek trojuholníka je vždy 180 °.

-Pre akýkoľvek trojuholník sa súčet jeho vonkajších uhlov rovná 360 °.

Môže vám slúžiť: Základný výskum: Charakteristiky, definície, príklady

- Vonkajší uhol trojuholníka sa rovná súčtu dvoch vnútorných uhlov, ktoré nie sú v susedstve tohto uhla.

Vety

Prvá veta takýchto

Pripisujú sa gréckym filozofom a matematikom Tales of Miletus, ktorý vyvinul niekoľko vety súvisiacich s geometriou. Prvý z nich stanovuje nasledujúce:

Ak niekoľko paralelných čiar odreže dve priečne čiary, určujú segmenty, ktoré sú proporcionálne.

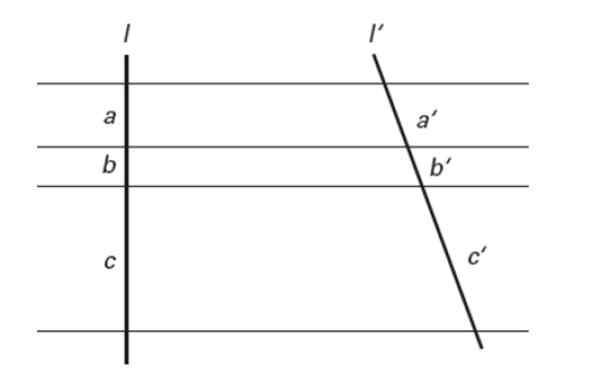Obrázok 7. Talesova veta. Zdroj: f. Zapata.

Inými slovami:

a/a '= b/b' = c/c '

Prvá veta, ktorá je taká, sa vzťahuje na trojuholník, napríklad na ľavej strane je modrý trojuholník ABC, ktorý je rezaný červenými paralelami doprava:

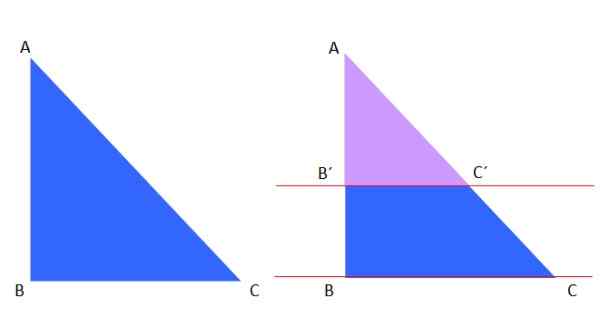Obrázok 8. Veta takýchto a podobných trojuholníkov.

Violet Triangle of Violet je podobný modrému trojuholníku ABC, a preto je možné podľa tejto vety napísať nasledujúce:

Ab '/ac' = ab/ac

A je to v súlade s tým, čo bolo vysvetlené vyššie v segmente podobnosti trojuholníkov. Mimochodom, paralelné čiary môžu byť tiež vertikálne alebo rovnobežné s hypotenusom a podobné trojuholníky sa získajú.

Druhá veta tohto

Táto veta sa tiež týka trojuholníka a obvodu centra alebo, rovnako ako tie, ktoré sú uvedené nižšie. Na tomto obrázku je AC priemerom obvodu a B je jeho bodom, ktorý sa líši od A a B.

Druhá veta takýchto štátov, že:

Uhol medzi segmentmi AB a BC je vždy 90 °, preto je trojuholník ABC obdĺžnik.

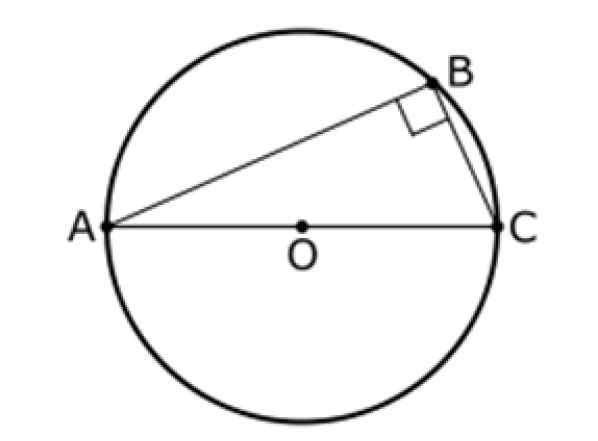Obrázok 9. Druhá veta takýchto. Zdroj: Wikimedia Commons. InduktiveLoad [verejná doména].

Pythagorová veta

Toto je jedna z najznámejších vety v histórii. Je to kvôli gréckym matematikom Pythagoras zo Samos (569 - 475 až. C.) a je použiteľný na pravý trojuholník. Hovorí áno:

Súčet štvorcov dĺžok kategórií obdĺžnika sa rovná dĺžke hypotenus vysokej ako štvorca.

Ak si uvedieme ako príklad modrý trojuholník na obrázku 8 alebo fialový trojuholník, pretože obidva sú obdĺžniky, potom sa dá povedať, že:

Ac² = Ab² + Bc² (Modrý trojuholník)

Ac '² = Ab '² + Bc '² (Fialový trojuholník)

Oblasť trojuholníka

Oblasť trojuholníka je daná produktom svojej základne do a jeho výška h, vydelené 2. A podľa trigonometrie možno túto výšku napísať ako H = b sinθ.

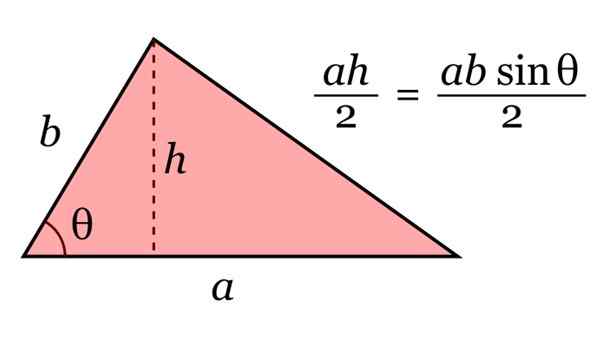Obrázok 10. Oblasť trojuholníka. Zdroj: Wikimedia Commons.

Príklady trojuholníkov

Príklad 1

Hovorí sa, že prostredníctvom svojej prvej vety sa takto podarilo zmerať výšku veľkej pyramídy v Egypte, jednej zo siedmich zázrakov starovekého sveta, meraním tieňa, ktorý premietal na zemi a ten, ktorý premieta do vkladu, v ktorej sa uviazli v porovnaní s vkladom zem.

Toto je schéma postupu, po ktorom nasleduje takáto:

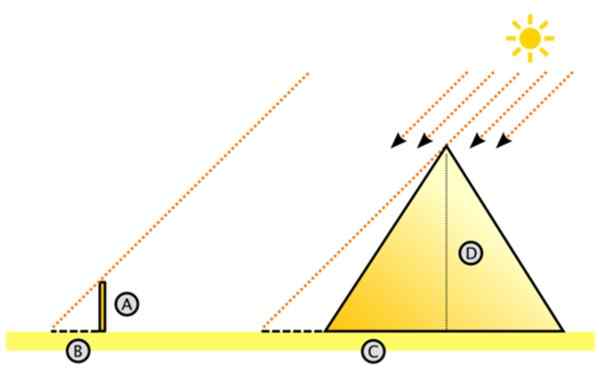Obrázok 11. Schéma na meranie výšky veľkej pyramídy podobnosťou trojuholníkov. Zdroj: Wikimedia Commons. Dake [CC By-SA 3.0 (http: // creativeCommons.Org/licencie/By-SA/3.0/]]

Takéto sa predpokladá, že slnečné lúče ovplyvňujú paralelne. S týmto vedomím si predstavoval trojuholník s pravou pravou.

Existuje výška pyramídy a C je vzdialenosť na zemi meraná od stredu po tieň vyčnievaný pyramídou na púštnej podlahe. Môže byť namáhavé merať C, ale je to určite jednoduchšie ako meranie výšky pyramídy.

Vľavo je malý trojuholník z mačiek A a B, kde A je výška vkladu uviaznutá vertikálne na podlahe a B je tieň, v ktorom projektuje. Obe dĺžky sú merateľné, rovnako ako C (C sa rovná dĺžke tieňa + polovica dĺžky pyramídy).

Môže vám slúžiť: Čo sú to hmatové podnety?

Potom podľa podobnosti trojuholníkov:

A/b = d/c

A výška veľkej pyramídy sa ukázala byť: d = c.(A/b)

Príklad 2

Civil Construction Armor sú konštrukcie založené na tenkých alebo kovových rovných tyčí, ktoré sa používajú ako podpora v mnohých budovách. Sú tiež známe ako mriežky, krovy alebo retikulované (Priehradka v angličtine).

V nich sú trojuholníky vždy prítomné, pretože tyče sú vzájomne prepojené v bodoch nazývaných uzly, ktoré môžu byť pevné alebo kĺbové.

Obrázok 12. Trojuholník je prítomný v ráme tohto mosta. Zdroj: pxhere.

Príklad 3

Metóda známa ako triangulácia vám umožňuje získať umiestnenie neprístupných bodov poznať ďalšie ľahšie vzdialenosti na meranie, pod podmienkou, že sa tvorí trojuholník, ktorý zahŕňa medzi jeho vrcholy požadované umiestnenie.

Napríklad na nasledujúcom čísle chcete vedieť, v akom okamihu je more loď označená ako b.

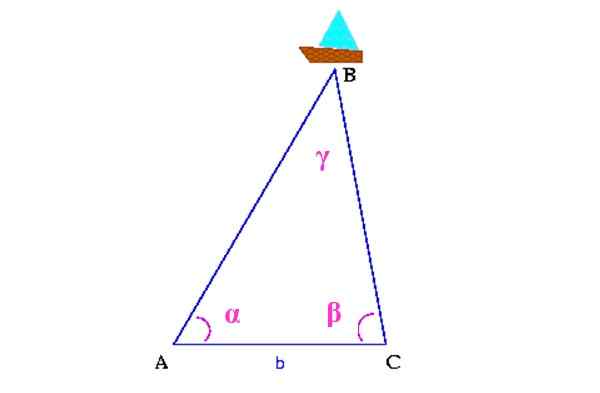Obrázok 13. Schéma triangulácie na lokalizáciu lode. Zdroj: Wikimedia Commons. Colette [CC BY-SA 3.0 (http: // creativeCommons.Org/licencie/By-SA/3.0/]]

Po prvé, meria sa vzdialenosť medzi dvoma bodmi na pobreží, ktoré na obrázku sú A a C. Potom musíte určiť uhly a a p pomocou a teodolit, Zariadenie, ktoré slúži na meranie vertikálnych a vodorovných uhlov.

So všetkými týmito informáciami je trojuholník postavený, na ktorom horným vrcholom je loď. Znížilo by to uhol γ, prostriedkom.

Cvičenia

Cvičenie 1

Na obrázku sú slnečné lúče rovnobežné. Týmto spôsobom 5 -meter vysoký strom vyčnieva 6 -meter tieň na zemi. V tom istom čase je tieň budovy 40 metrov. Po takejto vete takejto nájdite výšku budovy.

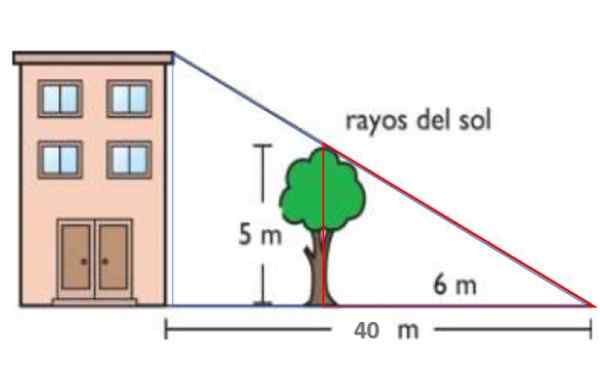Obrázok 14. Schéma pre rok vyriešená 1. Zdroj: f. Zapata.

Riešenie

Červený trojuholník má strany 5 a 6 metrov, zatiaľ čo modrá má výšku h - výšku budovy a základne 40 metrov. Oba trojuholníky sú preto podobné:

H / 40 = 5/6 → H = 40.(5/6) m = 33.3 m

Cvičenie 2

Musíte poznať vodorovnú vzdialenosť medzi dvoma bodmi Do a B, Ale nachádzajú sa vo veľmi nepravidelnom teréne.

Približne v strede (P_m) Z tejto krajiny vyniká význam 1.75 metrov vysoká. Ak opatrenie pásky naznačuje dĺžku 26 metrov meraných od A do významu a 27 metrov od B do toho istého bodu, nájdite vzdialenosť AB.

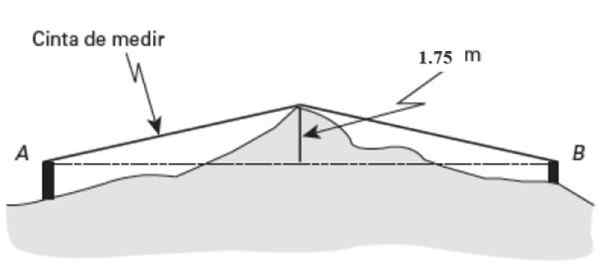Obrázok 15. Schéma pre cvičenie vyriešené 2. Zdroj: Jiménez, r. Matematika II. Geometria a trigonometria.

Riešenie

Veta Pythagoras sa aplikuje na jeden z dvoch obdĺžnikových trojuholníkov na obrázku. Počnúc tým vľavo:

Hypotenus = C = 26 metrov

Výška = a = 1.75 metrov

AP_m = (26² - 1.75²)^1/2 = 25.94 m

Teraz sa Pythagoras aplikuje v pravom trojuholníku, tentoraz c = 27 metrov, a = 1.75 metrov. S týmito hodnotami:

Bp_m= (27² - 1.75²)^1/2 = 26.94 m

Vzdialenosť AB pridáva tieto výsledky:

AB = 25.94 m +26.94 m = 52.88 m.

Odkazy

1. Baldor, J. Do. 1973.Geometria plochej a vesmíru. Stredoamerický kultúrny.
2. Barredo, D. Geometria trojuholníka. Získané z: ficus.pnent.Mec.je.
3. Jiménez, r. 2010. Matematika II. Geometria a trigonometria. Druhé vydanie. Pearson.
4. Wentworth, G. Geometria planéty. Získané z: Gutenberg.orgán.
5. Wikipedia. Trojuholník. Obnovené z: je. Wikipedia.orgán.