Tupý trojuholník

Vysvetlíme, čo je tupý trojuholník, jeho prvky, charakteristiky, typy, príklady a vyriešené cvičenie

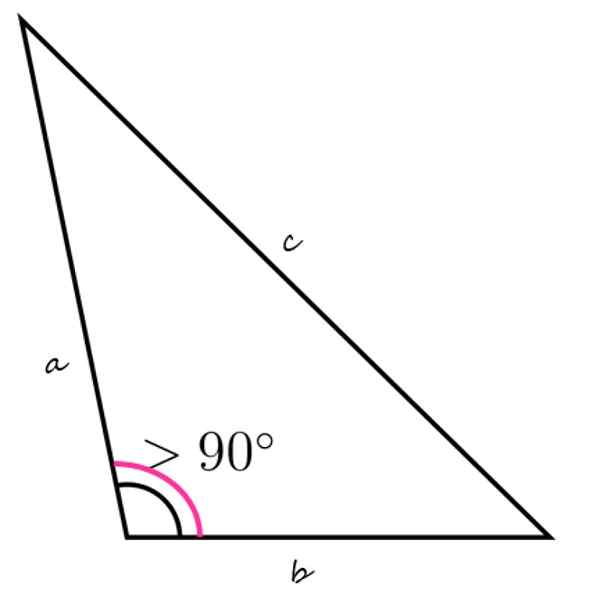Tupý trojuholník je charakterizovaný tým, že má vnútorný uhol väčší ako 90 °

Čo je tupý trojuholník?

A tupý trojuholník Je to plochá postava, uzavretá a s tromi stranami, ktoré tiež obsahujú tupý vnútorný uhol, to znamená väčší ako 90 ° a menej ako 180 °.

Každý trojuholník obsahuje 3 vnútorné uhly a ak je jeden z nich tupá, ďalšie dva sú silou, akútnou, pretože súčet vnútorných uhlov akéhokoľvek trojuholníka sa vždy rovná 180 °.

Horný obrázok zobrazuje príklad tupého trojuholníka, s ľavým vnútorným uhlom väčším ako 90 °. Zostávajúce vnútorné uhly musia pridať menej ako 90 °, iba týmto spôsobom je pravda, že súčet týchto troch sa rovná 180 °.

Okrem tupých trojuholníkov existujú aj akutangné trojuholníky, ak sú všetky jeho vnútorné uhly akútne a obdĺžnikové trojuholníky, keď jeden z vnútorných uhlov meria presne 90 °.

Prvky tupých trojuholníkov

Trojuholníky obtusángulos majú spoločné prvky pre všetky trojuholníky: sú to 3 -vedené ploché figúrky s 3 vnútornými uhlami a 3 vrcholmi. Okrem toho majú pozoruhodné segmenty, ktoré sa nazývajú Cevián, ako je výška, medián a mediatrix a body, kde sa ceviánci pretínajú.

Každý z týchto prvkov je stručne definovaný takto:

-Strany, sú segmenty, ktoré tvoria obrázok.

-Vrcholy, križovatka na každej pár susedných stranách.

-Vnútorné uhly, Sú medzi dvoma susednými stranami, na vnútornej strane obrázku, ktorá sa zhoduje s vrcholom uhla s uhlom trojuholníka.

-Vonkajšie uhly, Sú medzi jednou stranou a predĺžením susednej strany, mimo postavy, vrchol je bežný, a to z trojuholníka a uhla. Súčet opatrenia medzi vnútorným uhlom a jeho vonkajším susedným uhlom je 180 °, takže sú doplnkové uhly.

Môže vám slúžiť: Tukey Test: Čo je v prípade príkladu vyriešené cvičenie

-Výška, Je to miera kolmého segmentu, ktorý spája vrchol s opačnou stranou alebo s predĺžením tohto.

-Stredný, Čiara, ktorá je nasmerovaná zo vrcholu do stredu opačnej strany.

-Mediacia, segment kolmo na stranu a ktorý prechádza len cez jeho stred.

-Bisektor, Je to segment, ktorý sa delí na polovicu vnútorného uhla trojuholníka.

-Orocentro, križovatka v troch výškach.

-Barycenter, Tiež sa nazýva Centroid, je to bod, v ktorom sa tieto tri mediány pretínajú.

-Obvody, Tu sú strihané tri mediácie.

-Stimul, Bod bisektorov.

Po preskúmaní týchto konceptov sú uvedené niektoré z najvýznamnejších charakteristík tupých trojuholníkov nižšie.

Charakteristika

1.- Súčet troch vnútorných uhlov tupého trojuholníka je 180 °, preto iba jeden z jeho vnútorných uhlov môže byť väčší ako 90 °, zatiaľ čo súčet zostávajúcich dvoch je menší ako 90 °.

2.- Najdlhšia strana tupého trojuholníka je proti tupému uhlu.

3.- V tupom trojuholníku výšky z vrcholov, ktoré vytvárajú akútny uhol, prechádzajú predĺžením opačných strán.

4.- Ortocenter tupého trojuholníka je mimo obrázku.

5.- Z trojuholníka vypadne aj obvody tupého trojuholníka (k tomu nestane acutangle).

6.- Je možné zaregistrovať štvorec v tupom trojuholníku, ktorý podporuje jednu zo strán štvorca na najdlhšej strane trojuholníka. Môžu sa nakresliť dve štvorce, ktoré podopierajú stranu na najkratších stranách trojuholníka, čím sa vrchol nerešpektuje (ktorý sa nedotýka strany trojuholníka).

Môže vám slúžiť: Tidecágono

7.- Byť tupým trojuholníkom strán (a, b, c), ktorý je C najdlhšou stranou. Platí je to nasledujúca nerovnosť:

do²+b² < c²

8.- Sú to dva tupé trojuholníky, ktorých príslušné strany sú (a, b, c) a (u, v, w). Najdlhšie strany každého z nich sú C a W, takže sa splní nasledujúca nerovnosť:

A ∙ u + b ∙ v < c∙w

Typy brániacich trojuholníkov

Tupé trojuholníky môžu byť dvoch typov podľa dĺžky ich strán:

• Izoscely
• Vyskakovať

Sú stručne opísané nižšie:

Rovnoramenný trojuholník

Je to jedna, ktorá má dve rovnaké strany a iná, to znamená, že jeho strany sú (a, a, c).

Keď je Isosceles trojuholník tupý, strany merania „A“ sú kratšie a strana „C“ je najdlhšia. Uhol tupého uhla sa tvorí medzi rovnakými stranami, zatiaľ čo dva akútne uhly sú rovnaké a vytvárajú sa medzi stranymi „A“ a stranou „C“.

A ako je uvedené v predchádzajúcej časti, strana „C“, pretože je najdlhšia, je proti tupému uhlu.

Rôznostranný trojuholník

Tri strany Scalenovho trojuholníka majú odlišné meranie: (a, b, c).

Príklady

Príklad 1

Trojuholník znázornený na nasledujúcom obrázku je tupý. Tupý uhol je γ = 114.5. a je overené, že súčet troch vnútorných uhlov je 180 °:

114.5. + 36.8 ° + 28.6. ≈ 180 °

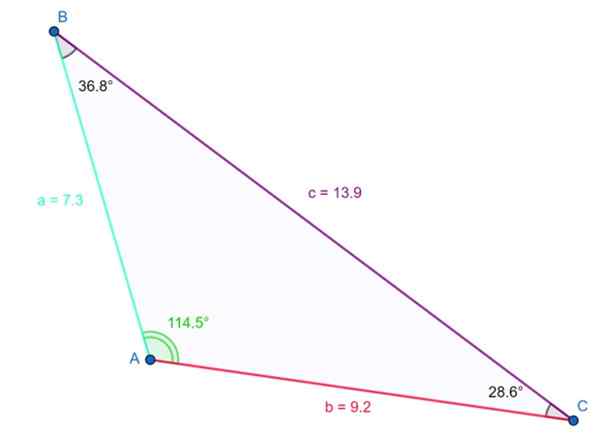Príklad tupého trojuholníka. Zdroj: f. Zapata

Najdlhšie vedľajšie opatrenia 13.9 jednotiek a je na rozdiel od tupého uhla. Splnená je aj vyššie uvedená nerovnosť:

do²+b² < c²

Môže vám slúžiť: Vzťahy proporcionality: koncept, príklady a cvičenia

ÁNO A = 7.3 a b = 9.2, potom:

7.3² + 9.2² < 13.9²

137.93 < 193.2

Príklad 2

V trojuholníku Calabi je možné umiestniť najväčší možný štvorec tromi rôznymi spôsobmi v trojuholníku, ako je znázornené na nasledujúcom obrázku.

Calabiho trojuholník je izoscely a tupé. Tupý uhol je približne 101.736 ° a akútne uhly na základni merajú obidve 39.13., tiež približne.

Cvičenie

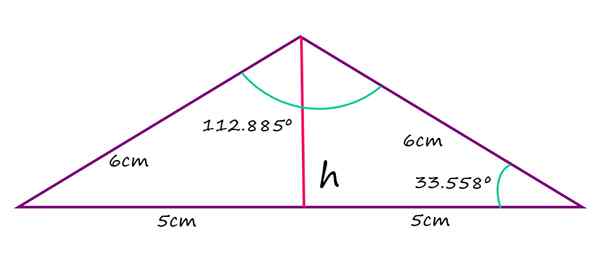
Rovnaké strany tupého trojuholníka Isosceles Meria 6 cm, zatiaľ čo najdlhšia bočná meria 10 cm. Vypočítajte hodnotu tupého uhla, hodnoty zostávajúcich uhlov Agudos a výšky od uvedeného vrcholu k základni.

Riešenie

Kozínová veta sa dá použiť na nájdenie kosínus tupého uhla. Potom s pomocou kalkulačky je určený príslušný uhol, označený ako y.

Cosenoova veta uvádza, že:

c² = a² +b² - 2ab ∙ cos γ

Kde y je uhol medzi stranami A a B. Pretože trojuholník sú izoscely, strany A a B sú rovnaké, preto:

c² = 2a² - 2²∙ cos γ

Clearing cos γ:

 Tupý uhol je oblúk Cosine -0.38889, čo je približne 112.885 °. Hodnota a, akútny uhol tvorený stranami 6 cm s 10 cm je:

2a + 112.885 ° = 180 °

a = (180 - 112.885)/2 = 33.558 °

Isosceles tupý trojuholník. Zdroj: f. Zapata

Pokiaľ ide o výšku trojuholníka, meraného zo základne, získa sa pozorovaním, že táto výška rozdeľuje trojuholník na dva rovnaké obdĺžniky, pričom hypotenusa sa rovná 6 cm a báza 5 cm. V takom prípade sa veta Pythagoras vzťahuje na priame nájdenie hodnoty H: