Trojuholník

Čo sú trojuholníky Acutangulus?

Ten Acutangulus trojuholníky Sú to tí, ktorých tri vnútorné uhly sú akútne uhly; to znamená, že miera každého z týchto uhlov je menšia ako 90 ° stupne. Tým, že nemáme žiadny pravý uhol, máme, že veta Pythagoras nie je pre túto geometrickú postavu splnená.

Preto, ak chceme mať nejaké informácie o ktorejkoľvek z jeho strán alebo uhlov, je potrebné používať iné vety, ktoré nám umožňujú mať prístup k týmto údajom. Tí, ktorých môžeme použiť, sú veta prsníka a kosínová veta.

Charakteristiky acutangleho trojuholníka

Medzi charakteristikami, ktoré má táto geometrická postava, môžeme zdôrazniť tie, ktoré sú dané jednoduchou skutočnosťou, že sú trojuholníkom. Medzi nimi musíme:

- Trojuholník je polygón, ktorý má tri strany a tri uhly.

- Súčet jeho troch vnútorných uhlov sa rovná 180 °.

- Súčet dvoch z jeho strán je vždy väčší ako tretí.

Ako príklad sa pozrime na nasledujúci trojuholník ABC. Vo všeobecnosti identifikujeme ich strany malým písmenom a ich uhlami s kapitálom, takže strana a ich opačný uhol majú rovnaké písmeno.

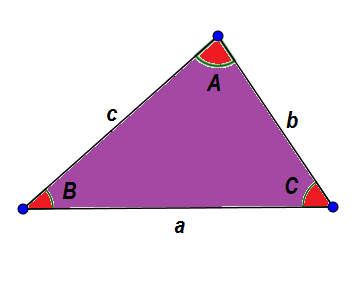
Z dôvodu, že už boli uvedené charakteristiky, vieme, že:

A + B + C = 180 °

A + b> c, a + c> b a b + c> a

Hlavnou charakteristikou, ktorá odlišuje tento typ trojuholníka od ostatných, je to, že, ako sme už spomenuli, jeho vnútorné uhly sú akútne; to znamená, že miera každého z jeho uhlov je menšia ako 90 °.

Acutangulus trojuholníky, spolu s tupými trojuholníkmi (tie, v ktorých má jeden z jeho uhlov meranie väčšie ako 90 °), sú súčasťou šikmej súpravy trojuholníkov. Táto súprava tvoria trojuholníky, ktoré nie sú obdĺžniky.

Môže vám slúžiť: Aké sú prvky podobenstva? (Časti)

Tým, že sme súčasťou šikmých trojuholníkov, musíme vyriešiť problémy, v ktorých Acutangulus Triangles zasahuje.

Veta

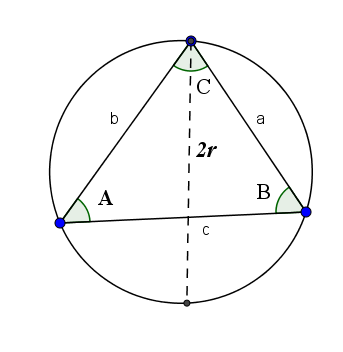
Veta prsníka potvrdzuje, že dôvod na jednej strane s lonom jeho opačného uhla sa rovná dvojnásobku polomeru kruhu tvoreného tromi vrcholmi uvedeného trojuholníka. To znamená:

2R = a/sin (a) = b/sen (b) = c/sen (c)

Coseno veta

Na druhej strane, Cosenoova veta nám dáva tieto tri rovnosti pre akýkoľvek trojuholník ABC:

do²= b² + c² -2BC*cos (a)

b²= a² + c² -2AC*cos (b)

c²= a² + b² -2ab*cos (c)

Tieto vety sú známe aj ako zákon sínusu a zákon Cosine, resp.

Ďalšou vlastnosťou, ktorú môžeme dať z akútnych trojuholníkov, je to, že dva z nich sú rovnaké, ak spĺňajú niektoré z nasledujúcich kritérií:

• Ak majú všetky tri strany.
• Ak majú stranu a dva uhly sa rovnajú navzájom.
• Ak majú dve strany a rovnaký uhol.

Typy trojuholníkov Acutángulos

Acutangulus trojuholníky možno klasifikovať podľa svojich strán. Môže to byť:

Trojuholníky rovnostranné acutangulos

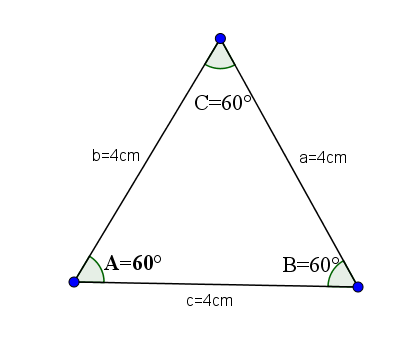
Sú to akcutangné trojuholníky, ktoré majú všetky svoje rovnaké strany, a preto všetky ich vnútorné uhly majú rovnakú hodnotu, čo je a = b = c = 60 ° stupne stupňov.

Ako príklad si vezmeme nasledujúci trojuholník, ktorého strany A, B a C majú hodnotu 4.

Isosceles Acutángulos trojuholníky

Tieto trojuholníky, okrem akútnych vnútorných uhlov, majú charakteristiku, že majú dve rovnaké strany a tretí, čo sa všeobecne berie ako základ.

Príkladom tohto typu trojuholníkov môže byť ten, ktorého základňa je 3 a jeho ďalšie dve strany majú hodnotu 5. S týmito opatreniami by mali uhly proti rovnakým stranám s hodnotou 72,55 ° a opačným uhlom základne by bol 34,9 °.

Môže vám slúžiť: Nulový uhol: Definícia a charakteristiky, príklady, cvičenia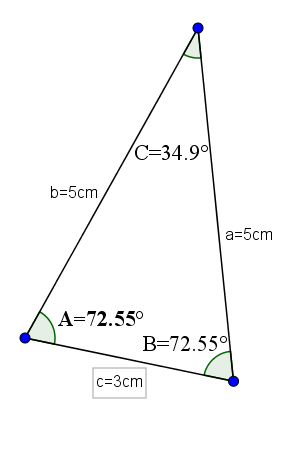

Scalen Acutangulus trojuholníky

Toto sú trojuholníky, ktoré majú všetky svoje rôzne strany dva až dve. Preto sú všetky jeho uhly, okrem toho, že sú menej ako 90 °.

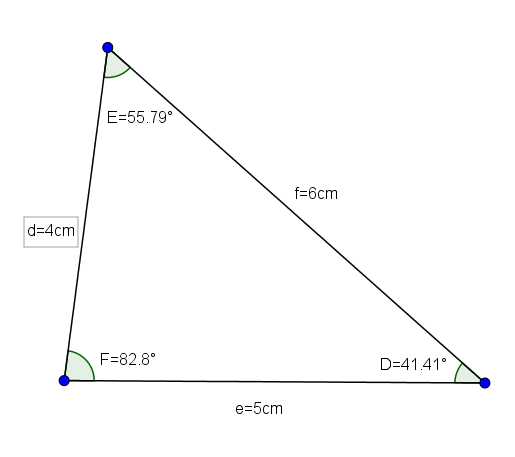
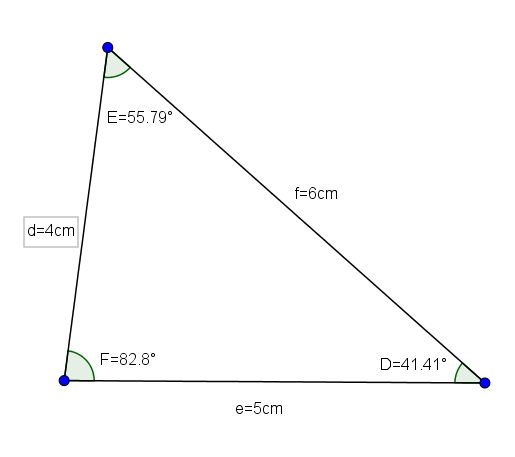
Triangle def (ktorého opatrenia sú d = 4, e = 5 a f = 6 a jeho uhly sú d = 41,41 °, E = 55,79 ° a F = 82,8 °) je dobrým príkladom akulgonického trojuholníka Scalene.

Rozlíšenie trojuholníkov

Ako sme už povedali, pre riešenie problémov, kde Acutangulus trojuholníky zasahujú.

Príklad 1

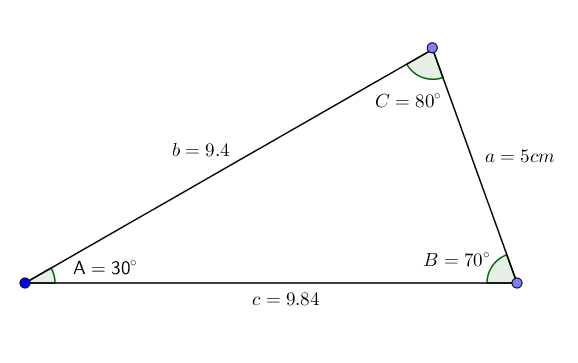
Vzhľadom na trojuholník ABC s uhlami a = 30 °, b = 70 ° a strana a = 5 cm, chceme poznať hodnotu uhla C a strán B a C.

Prvá vec, ktorú robíme, je použiť skutočnosť, že súčet vnútorných uhlov trojuholníka je 180 °, aby sa získala hodnota uhla C.

180 ° = a + b + c = 30 ° + 70 ° + c = 100 ° + c

Vyčistíme C a máme:

C = 180 ° - 100 ° = 80 °

Ako vieme, tri uhly a jedna strana, môžeme pomocou vety prsníka určiť hodnotu zvyšných strán. Pre vetu musíme:

a/sin (a) = b/sen (b) a a/sen (a) = c/(sin (c)

Vyčistíme rovnicu a musíme:

B = (a*sin (b))/sin (a) ≈ (5*0.940) / (0.5) ≈ 9.4

Teraz potrebujeme iba vypočítať hodnotu C. Postupujeme analogické, ako v predchádzajúcom prípade:

C = (a*sin (c))/sin (a) ≈ (5*0.984)/(0.5) ≈ 9.84

Preto dostávame všetky údaje o trojuholníku. Ako si všimneme, tento trojuholník vstupuje do kategórie skenovacieho trojuholníka.

Príklad 2

Vzhľadom na obranný trojuholník so stranami d = 4cm, e = 5 cm a f = 6cm, chceme poznať hodnotu uhlov uvedeného trojuholníka.

V tomto prípade použijeme zákon Cosine, ktorý nám hovorí:

Môže vám slúžiť: súčet štvorcov dvoch po sebe idúcich čísel

d²= e² + F² - 2EFCOS (D)

Z tejto rovnice môžeme vyčistiť cos (d), čo má za následok:

Cos (d) = ((4)² - (5)² -(6)²)/(-2*5*6) = 0.75

Odtiaľto musíme dotknúť 41.41 °

Pomocou vety Senom Teraz máme nasledujúcu rovnicu:

D/(sin (d) = e/(sin (e)

Clearing Sen (E), musíme:

sin (e) = e*sen (d)/d = (5*0.66)/4 ≈ 0.827

Odtiaľ musíme.79 °

Nakoniec, pomocou tohto súčtu vnútorných uhlov trojuholníka je 180 °, musíme.8 °.