Vlastnosti, vzťahy a vzorce Trapcio Isosceles, príklady

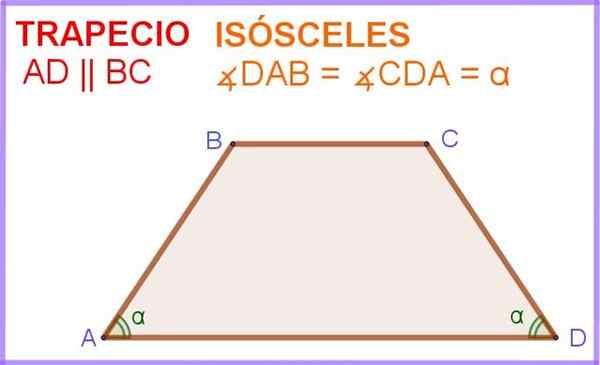
A lichobežník izoscely Je to štvoruholník, v ktorom sú dve strany navzájom rovnobežné a tiež dva uhly susediace s jednou z týchto rovnobežných strán majú rovnaké opatrenie.

Na obrázku 1 máte kvadrilaterálne ABCD, v ktorom sú strany AD a BC rovnobežné. Okrem toho uhly ∠DAB a ∠ADC susediace s paralelnou bočnou reklamy majú rovnaké opatrenie α. 

postava 1. Lichobežné izoscely. Zdroj: f. Zapata.

Tento kvadrilaterálny alebo štvorprúdový mnohouholník je v skutočnosti v skutočnosti lichobežník Isosceles.

V lichobežke sa rovnobežné strany nazývajú základne a nepaterély sa nazývajú bočný. Ďalšou dôležitou vlastnosťou je výška, čo je vzdialenosť, ktorá oddeľuje paralelné strany.

Okrem lichobežníka z izoscelov existujú aj ďalšie typy lichobežníkov:

-TónRapecio Escaleno, ktorý má všetky svoje rôzne uhly a boky.

-TónObdĺžnik Rapecio, v ktorom má strana priame priľahlé uhly.

Trapezoidálna forma je častá v rôznych oblastiach dizajnu, architektúry, elektroniky, výpočtu a mnohých ďalších, ako bude vidieť neskôr. Preto je dôležitosť oboznámenia sa od svojich vlastností.

[TOC]

Vlastnosti

Exkluzívny lichobežník Isosceles

Ak je lichobežník Isosceles, potom spĺňa nasledujúce charakteristické vlastnosti:

1.- Strany majú rovnaké opatrenie.

2.- Uhly susediace so základňami sú rovnaké.

3.- Opačné uhly sú doplnkové.

4.- Diagonály majú rovnakú dĺžku, rovnako ako dva segmenty, ktoré zjednocujú opačné vrcholy.

5.- Uhol tvorený medzi základňami a diagonálami je rovnaká miera.

6.- Obhajuje obvod.

Recipročne, ak lichobežník spĺňa niektoré z predchádzajúcich vlastností, potom je to lichobežník Isosceles.

Ak je v lichobežníkoch Isosceles jeden z uhlov rovný (90 °), potom budú všetky ostatné uhly tiež, tvoriaci obdĺžnik. To znamená, že obdĺžnik je konkrétny prípad lichobežníka Isosceles.

Obrázok 2. Kontajner kukurice palomitov a školské stoly sú tvarované ako izoscely. Zdroj: pxfuel (vľavo)/McDowell Craig cez Flickr. (správny)

Pre všetky lichobežníky

Nasledujúca sada vlastností je platná pre akékoľvek lichobežné:

7.- Ten stredný z lichobežníka, to je segment, ktorý sa spája so stredmi jeho nemaľujúcich strán, je rovnobežný s niektorou zo základní.

8.- Dĺžka mediánu sa rovná semi -sememum (súčet rozdelený 2) dĺžkou jeho základní.

9.- Medián lichobežníka prerušuje svoje diagonály v strede.

10.- Diagonály lichobežníka pretínajú v bode, ktorý ich rozdeľuje na dve časti úmerné kvocientom základní.

jedenásť.- Súčet štvorcov diagonálov lichobežníka sa rovná súčtu štvorcov jeho strán plus dvojitý produkt jeho základní.

Môže vám slúžiť: koľko tisícin sa zmestia do desiateho?

12.- Segment, ktorý sa pripojí k stredným bodom, má dĺžku rovnajúcu.

13.- Uhly susediace so stranami sú doplnkové.

14.- Trapeze má registrovaný obvod, ak a iba vtedy, ak sa súčet jeho základní rovná súčtu svojich strán.

pätnásť.- Ak má lichobežník registrovaný obvod, potom uhly s vrcholom v strede uvedeného obvodu a bočnými bokmi prechádzajúcimi koncami tej istej strany sú priame uhly.

Vzťahy a vzorce

Nasledujúci súbor vzťahov a vzorcov sa odvoláva na obrázok 3, kde okrem iSosceles lichobežníky, ktoré už boli uvedené ďalšie dôležité segmenty, ako sú diagonály, výška a médium.

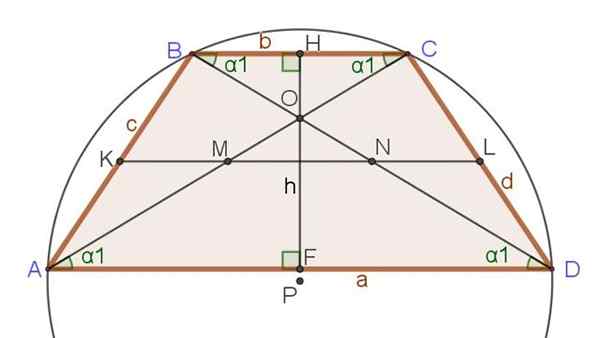Obrázok 3. Medián, diagonály, výška a obvod ohraničené v lichobežníku izosceles. Zdroj: f. Zapata.

Výlučné vzťahy Isosceles Tracecio

1.- Ab = dc = c = d

2.- ∡dab = ∡cda a ∡abc = ∡bcd

3.- ∡DAB + ∡BCD = 180 ° a ∡cda + ∡ABC = 180 °

4.- Bd = ac

5.- ∡cad = ∡bda = ∡cbd = ∡bca = α₁

6.- A, B, C a D patria k ohraničeným obvodom.

Vzťahy pre akýkoľvek lichobežník

7. Ak AK = KB a DL = LC ⇒ KL || AD a KL || Bc

8.- KL = (AD + BC)/2

9.- Am = mc = ac/2 a dn = nb = db/2

10.- AO/OC = ad/bc y do/ob = ad/bc

jedenásť.- Ac² + Db² = Ab² + Dc² + 2 ÁNDHL

12.- Mn = (Ad - Bc)/2

13.- ∡DAB + ∡ABC = 180 ° a ∡cda + ∡bcd = 180 °

14.- Ak AD + BC = AB + DC ⇒ ∃ R, čo Equidista AD, BC, AB a DC

pätnásť.- Ak ∃ r, čo Equidista AD, BC, AB a DC, potom:

∡bra = ∡drc = 90 °

Isosceles lichobežné vzťahy s registrovaným obvodom

Ak je v lichobežníku Isosceles, súčet báz sa rovná dvojnásobku strany, potom je tu registrovaný obvod.

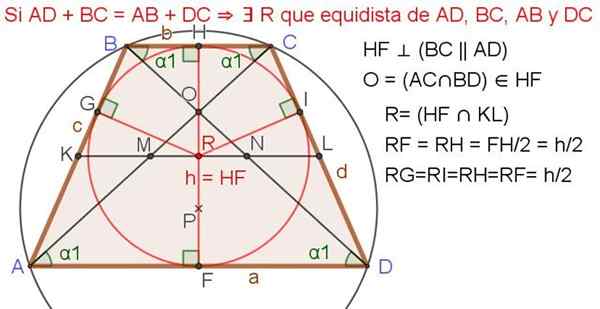Obrázok 4. Lichobežník s registrovaným obvodom. Zdroj: f. Zapata.

Ak má lichobežník Isosceles lichobežník registrovaný obvod (pozri obrázok 4 vyššie), uplatňujú sa nasledujúce vlastnosti (pozri obrázok 4):

16.- Kl = ab = dc = (ad + bc)/2

17.- Diagonaly sú rezané v pravom uhle: AC ⊥ BD

18.- Výška je rovnaká ako medián: hf = kl, to znamená h = m.

19.- Štvorec výšky sa rovná produktu základní: h² = Bc⋅ad

dvadsať.- Za týchto špecifických podmienok sa plocha lichobežky rovná štvorcovi výšky alebo produktu báz: oblasť = h² = Bc⋅ad.

Vzorce na určenie jednej strany, známe ostatné a uhol

Známy jeden základ, strana a uhol, druhý základ je možné určiť:

a = b + 2c cos α

B = a - 2c cos α

Ak je dĺžka báz známa ako známa a uhol, potom dĺžka oboch strán je:

Môže vám slúžiť: Fermat Limit: Čo pozostáva a cvičí vyriešené

C = (a - b) / (2 cos α)

Určenie na jednej strane, poznáte ostatných a diagonálne

A = (d₁² - c²)/ B;

B = (d₁² - c²)/ to 

C = √ (D₁² - A⋅b)

Kde d₁ Je to dĺžka diagonálov.

Základňa od výšky, oblasti a druhej základne

a = (2 a)/h - b

b = (2 a)/h - a

Známe späť základne, oblasť a uhol

C = (2a) /[(a + b) sin a]

Známy bočná medián, oblasť a uhol

C = a / (m.hriech α)

Známa výška bokov

H = √ [4 C² - (A - b)²]

Známa výška uhol a dve strany

H = TG a⋅ (a - b)/2 = c . hriech α

Známe diagonály všetky strany alebo dve strany a uhol

d₁ = √ (c²+ a b)

d₁ = √ (a²+ c² - 2 a c cos α)

d₁ = √ (b² + c²- 2 b c cos β)

Isosceles Triangle Perimeter 

P = a + b + 2c

Izosceles lichobežná oblasť

Existuje niekoľko vzorcov na výpočet oblasti v závislosti od známych údajov. V závislosti od báz a výšky je najznámejší:

A = H⋅ (A + B)/2

A tieto ďalšie je možné použiť:

-Ak sú známe strany

A = [(a +b)/4] √ [4c² - (A - b)²]

-Keď máte dve strany a uhol

A = (b + c cos α) c sen a = (a - c cos a) c sen α

-Ak je známy polomer registrovaného obvodu a uhol

A = 4 R² / Sin a = 4 r² / Sin β

-Keď sú známe základy a uhol

A = a⋅b / sin α = a⋅b / sen β 

-Ak je možné lichobežky zaregistrovať obvod

A = c⋅√ (a⋅b) = m kedy (a⋅b) = r⋅ (a + b)/2

-Známe diagonály a uhol, ktoré sa navzájom tvoria

A = (d₁²/2) Sen γ = (D₁² / 2) Sen δ 

-Keď máte stranu, medián a uhol

A = MC.Sin α = MC.Senátor

Ohraničené obvodové rádio

Iba lichobežné lichobežky majú ohraničený obvod. Ak je známa hlavná základňa, strana C a diagonálna D₁, Potom polomer R obvodu, ktorý prechádza štyrmi vrcholmi lichobežníka, je:

R = a⋅c⋅d₁ / 4√ [p (p -a) (p -c) (p -D₁)]

Kde p = (a + c + d₁) / 2

Príklady použitia lichobežníka Isosceles

Izosceles lichobežník sa objavuje v oblasti dizajnu, ako je vidieť na obrázku 2. A tu máme niekoľko ďalších príkladov:

V architektúre a výstavbe

Staroveká Inkovia poznali lichobežník Isosceles a použili ho ako stavebný prvok v tomto okne Cuzco, Peru:

Obrázok 5 . Okno s lichobežnou formou Coricancha, cuzco. Zdroj: Wikimedia Commons.

A tu sa lichobežník objaví opäť vo hovoru Lichobežník, Často používaný materiál pri konštrukcii:

Obrázok 6. Lichobežníkový kovový list dočasne chráni okná budovy. Zdroj: Wikimedia Commons.

Dizajn

Už sme videli, že lichobežník Isosceles sa objavuje v každodenných predmetoch, vrátane jedál, ako je táto čokoládová tyčinka:

Obrázok 7. Čokoládová tyčinka, ktorej tváre sú tvarované ako izoscely. Zdroj: pxfuel.

Vyriešené cvičenia

- Cvičenie 1

Izosceles lichobežník je založený ako 9 cm, báz menej ako 3 cm a každá jej diagonály 8 cm. Vypočítať:

Môže vám slúžiť: Všeobecná parabola rovnica (príklady a cvičenia)

a) Strana

b) výška

c) obvod

d) ärea

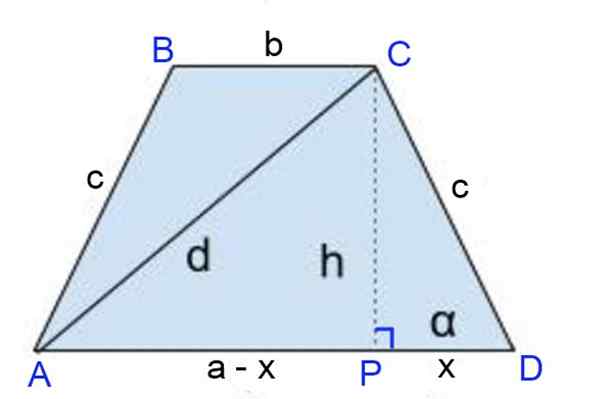Obrázok 8. Schéma cvičenia 1. Zdroj: f. Zapata

Roztok

Výška CP = H je nakreslená, kde noha výšky definuje segmenty:

Pd = x = (a-b)/2 a 

AP = a - x = a - a/2 + b/2 = (a + b)/2.

Prostredníctvom vety Pythagory na trojuholník DPC obdĺžnika:

c² = h² + (A - b)² /4

A tiež do trojuholníka APC obdĺžnika:

d² = h² + AP² = h² + (A+b)² /4

Nakoniec sa odpočíta člen, druhá rovnica prvej a zjednodušuje:

d² - c² = ¼ [(a+b)² - (A-b)²] = ¼ [(a+b+a-b) (a+b-a+b)]

d² - c² = ¼ [2a 2b] = a b

c²= d² - A b ⇒ c = √ (d² - a b) = √ (8² - 9 Á 3) = √37 = 6,08 cm

Riešenie B

h² = d² - (A+b)² /4 = 8² - (12² / 2² ) = 8² - 6² = 28

H = 2 √7 = 5,29 cm

Riešenie c

Obvod = A + B + 2 C = 9 + 3 + 2 šzerák 6,083 = 24 166 cm

Riešenie d

Oblasť = h (a+b)/2 = 5,29 (12)/2 = 31,74 cm

- Cvičenie 2

Existuje lichobežník Isosceles, ktorého najväčšia základňa je dvojnásobná a jeho najmenšia základňa sa rovná výške, ktorá je 6 cm. Určiť:

a) strana strany

b) obvod

c) oblasť

d) uhly

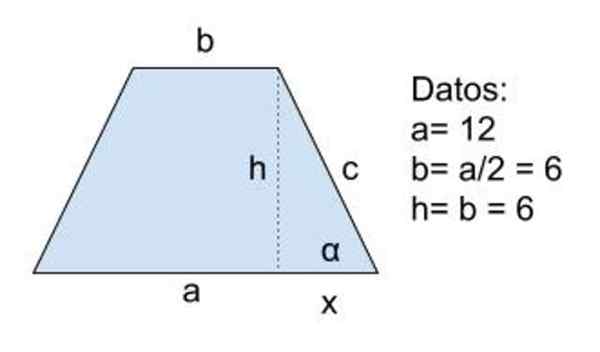Obrázok 8. Schéma cvičenia 2. Zdroj: f. Zapata

Roztok

Údaje: a = 12, b = a/2 = 6 a h = b = 6

Postupujeme týmto spôsobom: Výška H je nakreslená a veta Pythagorov sa aplikuje na hypotenusný trojuholník „C“ a Catetos H a X:

c² = h²+Xc²

Potom musíte vypočítať hodnotu výšky z údajov (H = B) a Cateto X: 

a = b + 2 x ⇒ x = (a-b)/2

Výmena predchádzajúcich výrazov, ktoré máte:

c² = b²+(A-b)²/2²

Teraz sa zavádzajú a zjednodušujú číselné hodnoty:

c² = 62+ (12-6) 2/4

c² = 62 (1+¼) = 62 (5/4)

Získanie:

C = 3√5 = 6,71 cm

Riešenie B

Obvod P = a + b + 2 c

P = 12 + 6 + 6√5 = 6 (8 + √5) = 61,42 cm

Riešenie c

Plocha založená na výške a dĺžke báz je:

A = H⋅ (a + b)/2 = 6 šcela (12 + 6)/2 = 54 cm²

Riešenie d

Uhol α, ktorý tvorí stranu s hlavnou základňou, sa získa trigonometriou:

Tan (a) = h / x = 6/3 = 2

a = arktan (2) = 63,44 °

Druhý uhol, ktorý tvorí stranu s menšou bázou, je β, ktorý je doplnkom α:

β = 180 ° - a = 180 ° - 63,44 ° = 116,56 °

Odkazy

1. A. Do. 2003. Elementy geometrie: s cvičeniami a geometria kompasu. University of Medellin.
2. Campos, f. 2014. Matematika 2. Redakčná skupina Patria.
3. Oslobodený, k. 2007. Objavovať polygóny. Benchmark vzdelávacia spoločnosť.
4. Hendrik, v. 2013. Zovšeobecnené polygóny. Birkhäuser.
5. Iger. Matematika Tacaná. Iger.
6. Jr. Geometria. 2014. Polygóny. Lulu Press, Inc.
7. Miller, Heeren a Hornsby. 2006. Matematika: uvažovanie a aplikácie. 10.  Vydanie. Pearson Vzdelanie.
8. Patiño, m. 2006. Matematika 5. Redakčný progreso.
9. Wikipedia. Lichobežník. Obnovené z: je.Wikipedia.com