Escaleno Trapezio Vlastnosti, vzorce a rovnice, príklady

A lichobežník vyskakovať Je to štvorprúdový polygón, z ktorých dva sú navzájom rovnobežné a so svojimi štyrmi vnútornými uhlami rôznych opatrení.

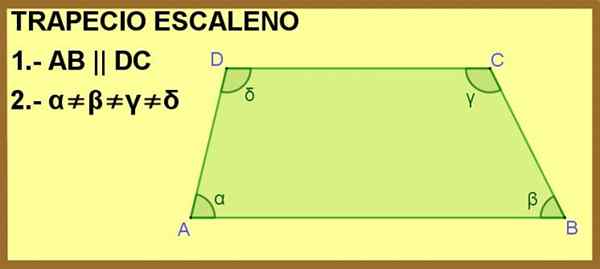
Zobrazuje sa ABCD Quadrilateral, kde sú strany AB a DC navzájom rovnobežné. S tým stačí urobiť z neho lichobežník, ale navyše sú vnútorné uhly a, β, y a δ rôzne, preto je lichobežník Escalano Escalano.

postava 1. ABCD Quadrilaterál je lichobežník pre podmienku 1 a Scalen pre podmienky 2. Zdroj: f. Zapata.

[TOC]

Prvky Scaleno Trachect

Pod najtvrdší prvky:

-Základne a strana: Paralelné strany lichobežníka sú jeho základy a dve nemagrované strany sú strany.

V ScaleNe Lapezio sú základy rôznej dĺžky a tiež boky. Avšak Scalen Lapezoid môže mať ako základňu rovnakú dĺžku.

-Medián: Je to segment, ktorý sa spája so stredmi strán.

-Diagonálne: Diagonál lichobežníka je segment, ktorý spája dva opačné vrcholy. Trapéza, rovnako ako každé kvadrilaterálne, má dve diagonály. V ScaleNe lichobezio majú inú dĺžku.

Ďalšie lichobežníky

Okrem Escaleno Trapezio existujú aj ďalšie osobitné lichobežníky: lichobežník obdĺžnika a lichobežník Isosceles.

Trapeze je obdĺžnik, keď je jeden z jeho uhlov rovný, zatiaľ čo lichobežné izosceles má svoje strany rovnakej dĺžky.

Trapezoidálna forma má početné aplikácie na dizajne a na úrovni priemyslu, napríklad v konfigurácii krídel lietadla, tvar každodenných predmetov, ako sú tabuľky, zálohy stoličiek, kontajnery, peňaženky, textilné výtlačky a ďalšie.

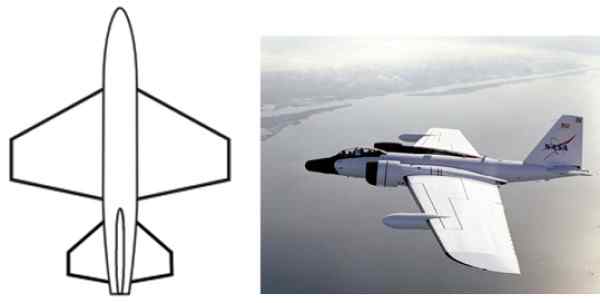Obrázok 2. Trapezoidálna forma je bežná v konfigurácii Alar Aircraft. Zdroj: Wikimedia Commons.

Vlastnosti

Ďalej sú uvedené vlastnosti lezeckého lichobežníka, z ktorých mnohé sú rozsiahle pre iné typy lichobežníkov. V nasledujúcom texte, keď hovoríte o „lichobežníku“, nehnuteľnosť sa bude vzťahovať na akýkoľvek druh, vrátane Scalenu.

1. Medián lichobežníka, to znamená segment, ktorý spája stredné body svojich nemaľujúcich strán, je rovnobežný s ktoroukoľvek zo základní.

2.- Medián lichobežníka má dĺžku, ktorá je semifinále jeho základne a prerezáva svoje diagonály v strede.

3.- Diagonály pretínania lichobežky v bode, ktorý ich rozdeľuje na dve časti, ktoré sú úmerné pomeru základní.

4.- Súčet štvorcov diagonálov lichobežníka sa rovná súčtu štvorcov jeho strán plus dvojitý produkt jeho základní.

5.- Segment, ktorý sa pripojí k stredným bodom, má dĺžku rovnajúcu.

Môže vám slúžiť: Injektívna funkcia: z čoho pozostáva, na čo ide a príklady

6.- Uhly susediace so stranami sú doplnkové.

7.- V Scalene Trapeze je dĺžka jeho uhlopriečok odlišná.

8.- Lapeze má registrovaný obvod iba vtedy, ak sa súčet jej základní rovná súčtu svojich strán.

9.- Ak má lichobežník zaregistrovaný obvod, potom je uhol so vrcholom v strede uvedeného obvodu a bokom, ktorý prechádza koncami bočného lichobera.

10.- Escaleno Trapeze nemá žiadny obvod, jediný typ lichobežníka, že ak má Is Isosceles.

Vzorce a rovnice

Nasledujúce vzťahy lezeckej lichobežky sú uvedené na nasledujúcom obrázku.

1.- Ak AE = ED a BF = FC → EF || AB a EF || Dc.

2.- Ef = (ab + dc)/2, to je: m = (a + c)/2.

3.- Di = ib = d₁ /2 a ag = gc = d₂ /2.

4.- Dj / jb = (c / a) podobne cj / ja = (c / a).

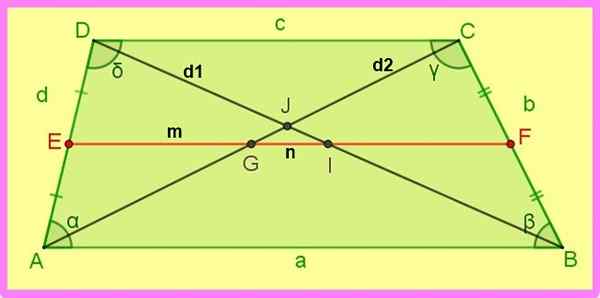Obrázok 3. Medián a diagonály z lapiča. Zdroj: f. Zapata.

5.- Db² + Ac² = Reklama² + Bc² + 2 ab ∙ dc 

Rovnocenne:

d₁² + d₂² = d² + b² + 2 a ∙ c

6.- Gi = (ab - dc)/2

To znamená:

n = (a - c)/2

7.- a + δ = 180⁰ a β + γ = 180⁰

8.- Ak α ≠ β ≠ γ ≠ Δ, potom d1 ≠ d2.

9.- Obrázok 4 zobrazuje ScaleNa lichobežníka, ktorý má registrovaný obvod, v takom prípade je splnené, že:

A + C = D + B

10.- V lichobežníku ABCD Escalene s registrovaným centrom centra alebo sa splní aj nasledujúce:

∡AOD = ∡Boc = 90⁰

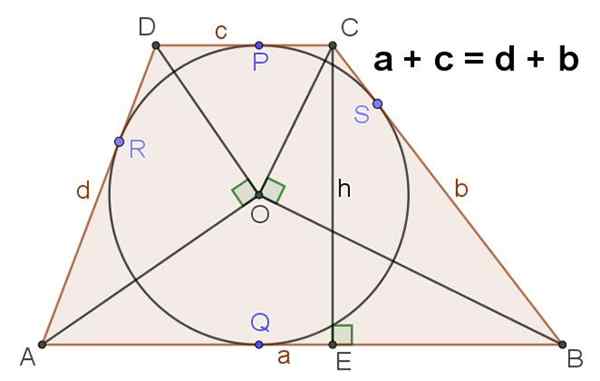Obrázok 4. Ak sa v lichobežke overuje, že súčet jeho základní sa rovná súčtu strán, potom je obvod vpísaný v rovnakom. Zdroj: f. Zapata.

Výška

Výška lichobežníka je definovaná ako segment, ktorý prechádza z bodu základne kolmo na opačný základ (alebo jeho rozšírenie).

Všetky výšky lichobežníka majú rovnaké opatrenie h, takže väčšinou výška slova sa vzťahuje na jeho meranie. Stručne povedané, výška je vzdialenosť alebo oddelenie medzi základňami.

Výška H je možné určiť, či je známa dĺžka strany a jeden z uhlov susediacich so bokom:

H = D Sin (a) = D Sin (γ) = B Sin (β) = B Sin (A)

Stredný

Stredná miera lichobežníka je semi -body základní:

M = (a + b)/2

Diagonála

d₁ = √ [a² + d² - 2 ∙ a ∙ d ∙ cos (α)]

d₂= √ [a² + b² - 2 ∙ a ∙ b ∙ cos (β)]

Dá sa tiež vypočítať, ak je známa iba dĺžka lichobežníka:

d₁ = √ [b² + A ∙ c - a (b² - d²)/(a - c)]

d₂ = √ [D² + A ∙ C - A (D² - b²)/(a - c)]

Obvod

Obvod je celková dĺžka obrysu, to znamená súčet všetkých jeho strán:

Môže vám slúžiť: diskrétna náhodná premenná

P = a + b + c + d

Oblasť

Oblasť lichobežníka je semifináles jej základní vynásobených jeho výškou:

A = h ∙ (a + b)/2

Dá sa tiež vypočítať, ak sú známe medián M a výška:

A = m ∙ h

V prípade, že je známa iba dĺžka lichobežníkových strán, oblasť je možné určiť Herónovým receptom pre lichobežník:

A = [(a+c)/| a-c |] ∙ √ [(s-a) (s-c) (S-a-d) (s-a-b)]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]

Kde s je poloperimeter: s = (a+b+c+d)/2.

Ostatné vzťahy pre lezenie

Výrez mediánu s diagonálmi a paralela, ktorá prechádza priesečníkom diagonálov, vedie k iným vzťahom.

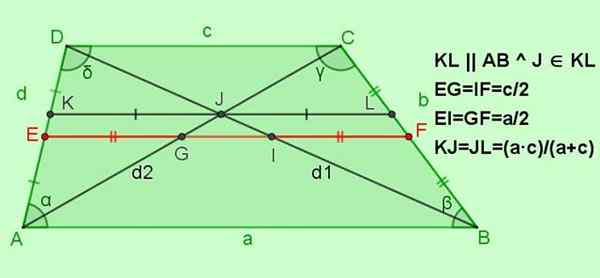Obrázok 5. Ostatné vzťahy pre lezenie. Zdroj: f. Zapata.

-Vzťahy pre stredný EF

Ef = (a+c)/2; Napr = if = c/2; Ei = gf = a/2

-Vzťahy pre paralelný segment so základňami KL a ktoré prechádzajú bodom Križovatka j diagonálov

Áno KL || AB || DC s j ∈ Kl, potom kj = jl = (a ∙ c)/(a+c)

Konštrukcia ScaleNa lichobežníka s pravidlom a kompasom

Vzhľadom na základy dĺžok do a c, byť> c a so stranou dĺžiek B a d, bytosť b> d, Postupujeme podľa týchto krokov (pozri obrázok 6):

1.- S pravidlom je nakreslený segment najväčšieho AB.

2.- Z SE a AB, bod P je označený tak, aby AP = C.

3.- S kompasom s C a Radio D Center je nakreslený oblúk.

4.- Je vyrobený v strede v B, pričom Rádio B kreslí oblúk, ktorý interpretuje oblúk vypracovaný v predchádzajúcom kroku. Hovoríme tomu priesečník.

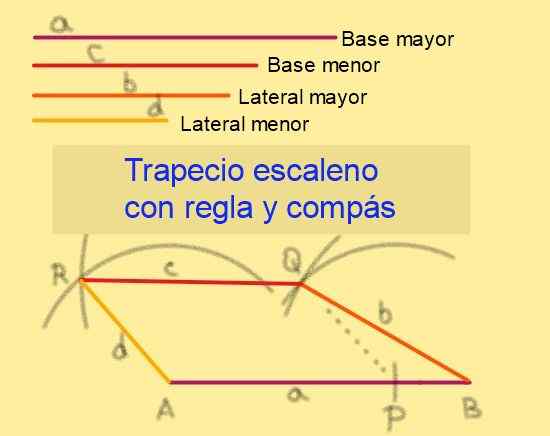Obrázok 6. Výstavba Escaleno Tracecio na jeho stranách. Zdroj: f. Zapata.

5.- So stredom pri nakreslení polomeru oblúk d.

6.- So stredom, v ktorom sa nakreslí oblúk polomeru, ktorý sa zachytil k oblúku, ktorý bol vypracovaný v predchádzajúcom kroku. Bude to nazývané R do bodu rezania.

7.- Segmenty BQ, QR a RA sú nakreslené pravidlom.

8.- ABQR Quadrilaterál je Scalen Lapezoid, pretože APQR je rovnobežník, ktorý zaručuje, že AB || QR.

Príklad

Nasledujúce dĺžky sú uvedené v cm: 7, 3, 4 a 6.

a) Určite, či s nimi môžete zostaviť Scalen Lapeze, ktorý dokáže obvod obvodu pripísať.

b) Nájdite obvod, plochu, dĺžku diagonálov a výšku uvedeného lichobežníka, ako aj polomer registrovaného obvodu.

- Roztok

Použitím segmentov dĺžky 7 a 3 ako základní a segmentov s dĺžkou 4 a 6 ako boky sa môže lachobežník vybudovať pomocou postupu opísaného v predchádzajúcej časti.

Musíme skontrolovať, či má registrovaný obvod, ale nezabudnite na vlastnosť (9):

Môže vám slúžiť: šesťuholníkový hranol

Lapeze má registrovaný obvod iba vtedy, ak sa súčet jej základní rovná súčtu svojich strán.

To skutočne vidíme:

7 + 3 = 4 + 6 = 10

Potom je splnený stav vpísaného obvodu.

- Riešenie B

Obvod

Obvod P sa získa pridaním strán. Keďže základy sú celkom 10 a boky, obvod je:

P = 20 cm

Oblasť

Na určenie oblasti je známy iba jej strany, vzťah sa uplatňuje:

A = [(a+c)/| a-c |] ∙ √ [(s-a) (s-c) (S-a-d) (s-a-b)]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]

Kde s je poloperimeter:

S = (a+b+c+d)/2.

V našom prípade má poloperimeter hodnotu s = 10 cm. Po výmene príslušných hodnôt:

A = 7 cm; B = 6 cm; C = 3 cm; D = 4 cm

Zostane:

A = [10/4] √ [(3) (7) (-1) (-3)] = (5/2) √63 = 19,84 cm².

Výška

Výška H súvisí s oblasťou A cez nasledujúci výraz:

A = (a+c) ∙ h/2, kde výška je možné získať vôľou:

H = 2a / (a+c) = 2 * 19,84 / 10 = 3 968 cm.

Registrované obvodové rádio

Polomer registrovaného obvodu má polovicu výšky:

R = h/2 = 1 984 cm

Diagonála

Nakoniec je tu dĺžka diagonálov:

d₁ = √ [b² + A ∙ c - a (b² - d²)/(a - c)]

d₂ = √ [D² + A ∙ C - A (D² - b²)/(a - c)]

Správne nahradenie hodnôt sú:

d₁ = √ [6² + 7 ∙ 3 - 7 (6² - 4²)/(7 - 3)] = √ (36+21-7 (20)/4) = √ (22)

d₂ = √ [4² + 7 ∙ 3 - 7 (4² - 6²)/(7-3)] = √ (16+21-7 (-20)/4) = √ (72)

To znamená: D₁ = 4,69 cm a D₂ = 8,49 cm

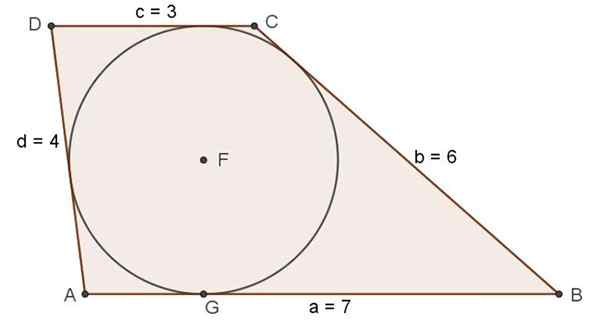Obrázok 7. Scale Lapezio, ktoré spĺňa stav existencie registrovaného obvodu. Zdroj: f. Zapata.

Cvičenie

Určte vnútorné uhly základného lichobežníka AB = A = 7, CD = C = 3 a laterálne BC = B = 6, DA = D = 4.

Riešenie

Na určenie uhlov môže byť použitá kosínová veta. Napríklad uhol ∠A = a je určený z trojuholníka ABD s AB = A = 7, BD = D2 = 8,49 a DA = D = 4.

Kozínová veta aplikovaná na tento trojuholník zostáva takto:

d₂² = a² + d² - 2 ∙ a ∙ d ∙ cos (α), to znamená:

72 = 49+16-56 ∙ cos (a).

Pri vyčistení sa získa kosínus uhla a:

Cos (a) = -1/8

To znamená, že a = arccos (-1/8) = 97,18⁰.

Rovnakým spôsobom sa získavajú ostatné uhly, ktoré sú ich hodnotami:

β = 41,41⁰; γ = 138,59⁰ a nakoniec δ = 82,82⁰.

Odkazy

1. C. A. Do. (2003). Elementy geometrie: s cvičeniami a geometria kompasu. University of Medellin.
2. Campos, f., Cerecedo, f. J. (2014). Matematika 2. Redakčná skupina Patria.
3. Oslobodený, k. (2007). Objavovať polygóny. Benchmark vzdelávacia spoločnosť.
4. Hendrik, v. (2013). Zovšeobecnené polygóny. Birkhäuser.
5. Iger. (s.F.). Matematika Tacaná. Iger.
6. Jr. Geometria. (2014). Polygóny. Lulu Press, Inc.
7. Miller, Heeren a Hornsby. (2006). Matematika: uvažovanie a aplikácie (desiate vydanie). Pearson Vzdelanie.
8. Patiño, m. (2006). Matematika 5. Redakčný progreso.
9. Wikipedia. Lichobežník. Obnovené z: je.Wikipedia.com