Fourier Discreet Transformované vlastnosti, aplikácie, príklady

Ten Fourier Discreet sa transformoval Je to numerická metóda použitá na definovanie vzoriek súvisiacich so spektrálnymi frekvenciami, ktoré tvoria signál. Študuje periodické funkcie v uzavretých parametroch a hádzajú v dôsledku toho ďalší diskrétny signál.

Aby sa získala diskrétna transformácia Furier z n bodov, na diskrétnom signáli sa musia splniť nasledujúce 2 podmienky v sekvencii X [n]

 x [n] = 0   N n - 1

Plnenie týchto podmienok, diskrétna transformácia Fourier môže byť definovaná ako

TDF

Fourierova diskrétna transformácia možno definovať ako odber vzoriek v n bodom Fourierovej transformácie.

[TOC]

Interpretácia Fourierovej diskrétnej transformácie

Zdroj: pexels

Existujú 2 body, z ktorých je možné interpretovať výsledky získané v sekvencii x_siež[n] Prostredníctvom Fourierovej diskrétnej transformácie.

-Prvý zodpovedá spektrálnym koeficientom, ktoré už sú známe sérii Fourier. Pozoruje sa v diskrétnych periodických signáloch, pričom vzorky sa zhodujú so sekvenciou x_siež[N].

-Druhý je o spektre diskrétneho aperiadického signálu, pričom vzorky zodpovedajú sekvencii x_siež[N].

Diskrétna transformácia je prístup k spektru pôvodného analógového signálu. Jeho fáza závisí od momentov odberu vzoriek, zatiaľ čo jeho veľkosť závisí od intervalu odberu vzoriek.

Vlastnosti

Algebraické základy štruktúry tvoria logický základ nasledujúcich častí.

Linearita

C . Siež_n → C . F [Siež_{klimatizovať}]; Ak sa sekvencia vynásobí skalárnym, jej transformácia bude tiež.

Tón_n + Vložka_n = F [t_{klimatizovať}]+F [v_{klimatizovať}]; Transformácia súčtu sa rovná súčtu transformovaných.

Dualita

F [s_n] → (1/n) s_-K; Ak je diskrétna transformácia Fourier odvolaná na už transformovanú expresiu, získa sa rovnaký výraz, lezenie v n invertovanom vzhľadom na vertikálnu os.

Konvolúcia

Prenasledovanie podobných cieľov, ktoré sa v Laplace transformujú, konvolúcia funkcií sa vzťahuje na produkt medzi jeho Fourier Transforps. Konvolúcia sa vzťahuje aj pre diskrétne časy a je zodpovedná za mnoho moderných postupov.

X_n * R_n → f [x_n] .F [r_n]; Transformácia konvolúcie sa rovná produktu transformovaných.

X_n . R_n→ f [x_n] * F [r_n]; Transformácia produktu sa rovná konvolúcii transformovaných.

Posunutie

X_N-m → f [x_{klimatizovať}] e ^{-I (2π/n) km} ; Ak je postupnosť oneskorená vo vzorkách M, jeho účinok na diskrétnu transformáciu bude modifikáciou uhla definovaného (2π/n) km.

Môže vám slúžiť: Prečo je algebra dôležitá v určitých každodenných situáciách?

Symetria konjugovaný

X_tón [-K] = x*_tón[k] = x_tón [N - k]

Modulácia

W^-nm_N . x [n] ↔ x_tón[K - m]

Produkt

x [n] y [n] ↔ (1/n) x_tón[k]*a_tón[K]

Symetria

X [-n] ↔ x_tón[-K] = x*_tón[K]

Zjavný

x*[n] ↔ x*_tón[-K]

Parseval rovnica 

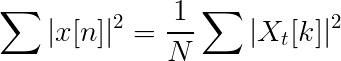
Podobnosti a rozdiely s Fourierovou transformáciou

Pokiaľ ide o konvenčnú transformáciu Fourierovej, má niekoľko podobností a rozdielov. Fourierova transformácia prevádza sekvenciu na kontinuálnu čiaru. Týmto spôsobom sa hovorí, že výsledkom Fourierovej premennej je zložitá skutočná premenná funkcia.

Fourierova diskrétna transformácia, na rozdiel od, dostáva diskrétny signál a transformuje ho na ďalšie diskrétne znamenie, to znamená sekvencia.

Aké je použitie Fourierovej diskrétnej transformácie?

Slúžia hlavne významným rovniciam, pričom transformujú výrazy odvodené na energetické prvky. Označovanie diferenciálnych výrazov vo formách integrovateľných polynómov.

Pri optimalizácii, modulácii a modelovaní výsledkov pôsobí ako štandardizovaný výraz, ktorý je častým zdrojom pre inžinierstvo po niekoľkých generáciách.

Zdroj: Pixabay

História

Tento matematický koncept predstavil Joseph B. Fourier v roku 1811, zatiaľ čo rozvíja zmluvu týkajúcu sa Roztiahnutie tepla. Rýchlo ho prijali rôzne odvetvia vedy a inžinierstva.

Bol založený ako hlavný pracovný nástroj v štúdiu rovníc s čiastočnými derivátmi, v porovnaní s pracovným vzťahom medzi Laplace transformované a bežné diferenciálne rovnice.

Akákoľvek funkcia, ktorú je možné prepracovať s Fourierovou transformáciou, musí predstavovať neplatnosť mimo definovaného parametra.

Fourier Discreet sa transformoval a jeho inverzná

Diskrétna transformácia sa získa výrazom:

Po diskrétnej sekvencii x [n]

Inverzia Fourierovej diskrétnej transformácie je definovaná výrazom:

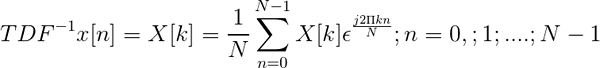Inverzný TDF

Umožňuje, keď sa diskrétny transformuje, definujte sekvenciu v časovej doméne x [n].

Lesklý

Proces parametrizácie zodpovedajúci Fourierovej diskrétnej transformácii leží v mláďa. Aby sme pracovali na transformácii, musíme v čase obmedziť sekvenciu. V mnohých prípadoch tieto obmedzenia nemajú tieto obmedzenia.

Postupnosť, ktorá nespĺňa kritériá veľkosti, ktoré sa vzťahujú na diskrétnu transformáciu, sa dá vynásobiť funkciou „okna“ v [n], ktorá definuje správanie dedenia v riadenom parametri.

Môže vám slúžiť: kruhové permutácie: demonštrácia, príklady, vyriešené cvičenia

X [n] . V [n]

Šírka spektra bude závisieť od šírky okna. Keď sa zvyšuje šírka okna, vypočítané transformované bude užšie.

Žiadosti

Výpočet základného riešenia

Fourierova diskrétna transformácia je výkonným nástrojom pri štúdiu diskrétnych úspechov.

Fourierova diskrétna transformácia transformuje kontinuálnu premennú funkciu na diskrétnu premennú transformáciu.

Problém Cauchy pre tepelnú rovnicu predstavuje časté pole aplikácie Fourierovej diskrétnej transformácie. Kde sa generuje funkcia Dirichlet Heat alebo jadro jadra, ktorý sa vzťahuje na odber vzoriek hodnôt v definovanom parametri.

Teória signálu

Všeobecný dôvod uplatňovania Fourierovho diskrétnej transformácie v tejto vetve je väčšinou spôsobený charakteristickým rozkladom signálu ako nekonečného prekrývania ľahšie liečiteľných signálov.

Môže to byť zvuková vlna alebo elektromagnetická vlna, Fourierove diskrétna transformácia ju vyjadruje v jednoduchej prekrývaní vlny. Táto reprezentácia je v elektrotechnike pomerne častá.

Fourierova séria

Sú definované série z hľadiska cosenos a prsia. Slúžia na uľahčenie práce so všeobecnými periodickými funkciami. Pri použití sú súčasťou techník rozlíšenia čiastočných a bežných diferenciálnych rovníc.

Fourier Series je ešte všeobecnejší ako séria Taylor, pretože vyvíjajú periodické funkcie diskontinua, ktoré nemajú žiadne zastúpenie v sérii Taylor.

Ostatné formy série Fourier

Analyticky porozumieť Fourierovej transformácii je dôležité.

-Fourier Series na funkcii 2L obdobia:

Mnohokrát je potrebné prispôsobiť štruktúru Fourierovej série na periodické funkcie, ktorých obdobie je p = 2l> 0 v intervale [-l, l].

-Fourier Series v párnych a nepárnych funkciách

Zvažuje sa interval [-π, π], ktorý ponúka výhody pri využívaní symetrických charakteristík funkcií.

Môže vám slúžiť: konečná súprava: Vlastnosti, príklady, vyriešené cvičenia

Ak F je krútiaci moment, séria Fourier je zriadená ako séria Cosenosu.

Ak je F nepárne, séria Fourier je zriadená ako séria prsníkov.

-Komplexná notácia série Fourier

Ak máte funkciu F (t), ktorá spĺňa všetky požiadavky série Fourier, je možné ju označiť v intervale [-T, t] pomocou svojej komplexnej zápisu: 

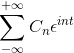
Príklady

Pokiaľ ide o výpočet základného riešenia, sú uvedené nasledujúce príklady:

Laplaceová rovnica

Tepelná rovnica

Schrödingerova rovnica

Vlnová rovnica

Na druhej strane existujú príklady použitia Fourierovej diskrétnej transformácie v oblasti teórie signálu:

-Problémy s identifikáciou systému. Zavedené f a g

-Problém s konzistentnosťou výstupného signálu

-Problémy s filtrovaním signálu

Cvičenia

Cvičenie 1

Vypočítajte Fourierovu diskrétnu transformáciu pre nasledujúcu sukcesiu.

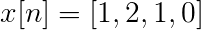
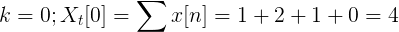
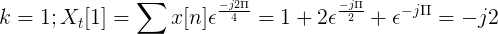
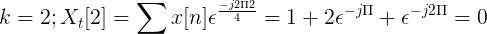
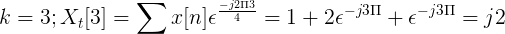
X [n] TDF možno definovať ako:

X_tón[k] = 4, -j2, 0, j2 pre k = 0, 1, 2, 3

Cvičenie 2

Prostredníctvom digitálneho algoritmu je potrebné určiť spektrálny signál definovaný výrazom x (t) = e^-tón. Kde maximálna frekvencia požadujúca koeficient F je f_m= 1 Hz. Harmonika zodpovedá F = 0.3 Hz. Chyba je obmedzená na menej ako 5%. Vypočítať F_siež , D a n.

Berúc do úvahy vetu odberu vzoriek F_siež = 2f_m = 2 Hz

Frekvenčné rozlíšenie F₀ = 0.1 Hz, kde sa získajú d = 1/0,1 = 10s

0.3 Hz je frekvencia zodpovedajúca indexu k = 3, kde n = 3 × 8 = 24 vzoriek. Naznačujúc to F_siež = N/d = 24/10 = 2.4> 2

Pretože účelom je dosiahnuť najmenšiu možnú hodnotu pre n, za riešenie možno považovať nasledujúce hodnoty:

F₀ = 0.3 Hz

D = 1/0.3 = 3.33s

K = 1

N = 1 × 8 = 8

Odkazy

1. Zvládnutie diskrétnej Fourierovej transformácie v jednej, dve alebo viacerých dimenziách: nástrahy a artefakty. Izák Amidor. Springer Science & Business Media, 19. júla. 2013
2. DFT: Príručka vlastníkov pre diskrétnu Fourierovu transformáciu. William L. Briggs, Van Emden Henson. Siam, 1. januára. Devätnásť deväťdesiatpäť
3. Spracovanie digitálneho signálu: teória a prax. D. Sundararajan. World Scientific, 2003
4. Transformácie a rýchle algoritmy na analýzu a reprezentácie signálu. Guoan BI, Yonghong Zeng. Springer Science & Business Media, 6. decembra. 2012
5. Diskrétne a kontinuálne Fourierové transformácie: analýza, aplikácie a rýchle algoritmy. Eleanor Chu. CRC Press, 19. 2008