Vlastnosti lineárnych transformácií, aké sú použitie, typy, príklady

A Lineárna transformácia, ktoré jednoducho zavoláme, súvisí s prvkami dvoch vektorových priestorov v a w, priraďovanie každého vektora vložka patriace k v jednom vektore W ktorý patrí W, prostredníctvom konkrétnej operácie.

Táto transformácia spĺňa dve podmienky:

postava 1. Lineárna transformácia sa vzťahuje na vektor vektorového priestoru V, aby sa získal ďalší vektor patriaci k vektorovému priestoru W. Zdroj: f. Zapata.

-Stav 1

Vzťahuje sa na pridanie, takže t -lineárna transformácia sa musí splniť:

T (vložka + W) = T (vložka) + T (W)

-Stav 2

Druhá podmienka predstavuje homogenitu v násobení skalárneho vektorom:

T (cvložka) = c⋅t (vložka)

Lineárna transformácia, ako už názov napovedá, je zodpovedná za mapovanie alebo transformáciu prvkov V na prvky w.

Zápis funkcií sa používa aj v prípade lineárnych transformácií, takže doména V je sada prvkov (vektorov), ktoré sa majú transformovať, zatiaľ čo kodomínium alebo trasa je výslednou množinou.

Príklad lineárnej transformácie je:

Na označenie, že písmeno T sa použije. Transformácia sa použije na vektor vložka ktorých komponenty sú x a y, ktoré boli reprezentované jednou stĺpcovou maticou. Výsledkom je ďalší vektor W ktorých komponenty sú x a 0, tiež reprezentované maticou stĺpca.

Preto je to transformácia vektorového priestoru r² Smerom k vektorovému priestoru r², Zhrnutie je napísané takto:

T: R² → R²         

Ak máme vektor:

Transformácia nás vracia:

A tak s akýmkoľvek R vektorom². V príklade 1 sa overí, že táto transformácia je lineárna.

[TOC]

Vlastnosti lineárnych transformácií

Predpokladajme lineárnu transformáciu V vo W, v ktorej vektory vložka a alebo Patria k V, potom sú splnené nasledujúce vlastnosti:

Nehnuteľnosť 1

T (0) = 0

Kde 0 je nulový vektor.

Nehnuteľnosť 2

T (-vložka) = - t (vložka)

Nehnuteľnosť 3

T (alebo  - vložka) = T (alebo) - t (vložka)

Nehnuteľnosť 4

Byť vložka = c₁vložka₁ + c₂vložka₂ +.. . +  c_nvložka_n

 Tak:

T (c₁vložka₁ + c₂vložka₂ +.. . +  c_nvložka_n) = c₁ T (vložka₁) + c₂ T (vložka₂) +.. . +  c_n T (vložka_n)

Prvky lineárnej transformácie

Nech V a W už spomínané vektorové priestory, kde lineárna transformácia T transformuje prvky V na w. Môžeme definovať tieto prvky:

-C jadro alebo jadro: Je to podskupina domény, ktorej je označená N (t) ani Ker (T) a porozumieť všetkým prvkom v tak, že:

T (vložka) = 0.

Lineárna transformácia t (vložka) = 0 sa volá nulová transformácia.

Prirodzene nulový vektor vložka = 0 napriek tomu sa naplní s týmto stavom, ale jadro pozostáva z celých ne -nulových vektorov, ktoré ho tiež spĺňajú, pre danú t.

Môže vám slúžiť: Rastúca funkcia: Ako ju identifikovať, príklady, cvičenia

-Obraz t: Je to sada vektorov patriacich k W, ktoré sú obrazom aspoň nejakého vektora vo V. Je označený ako Im t) A je to podmnožina vektorového priestoru W.

Tieto prvky nám pomôžu klasifikovať lineárne transformácie neskôr.

Čo sú lineárne transformácie pre?

Spočiatku lineárne transformácie fungujú s vektorovými priestormi, ktoré tvoria vektory. Mnohokrát spájame vektory so silou a inými fyzikálnymi veľkosťami, avšak pri spracovaní digitálneho obrazu môže byť pixel reprezentovaný vektorom.

V takom prípade je možné s obrazom manipulovať pohodlnými lineárnymi transformáciami, aby sa získali požadované efekty, napríklad premietanie, otáčanie, nájdenie zrkadlového obrazu alebo úpravy jeho veľkosti bez zmeny relatívnych rozmerov.

Lineárne transformácie sa tiež široko používajú v ekonómii a rozhodovaní, napríklad na poznanie množstva surovín potrebných na výrobu určitej dávky produktu.

Počet kusov potrebných na zostavenie rôznych modelov vyrobených továrňou je možné prepracovať prostredníctvom usporiadania matrice, ako uvidíme neskôr.

Typy lineárnych transformácií (klasifikácia)

Rovnako ako funkcie, aj lineárne transformácie môžu byť:

-Injekčné alebo monomorfizmy

-Bijekcie alebo Epimorfizmus

-Nadmerné alebo Izomorfizmy

Okrem toho sú nasledujúce typy:

-Endomorfizmy

-Automorfizmy.

Injekčné lineárne transformácie

Nech V a W vektorové priestory a t a lineárna transformácia t: v → w. T je injekčné, keď:

Ker (T) = 0

Lineárne prevodné transformácie

Ak sú V a W vektorové priestory tak, že T: V → W, hovorí sa, že T je bijektívny, keď:

Im (t) = w

Bijjektívne lineárne transformácie

Lineárna transformácia T: V → W je bijective, keď je injekčná a nadmerná. Preto je splnené, že:

Ker (T) = 0 a Im (t) = w

Endomorfizmy

Sú to lineárne transformácie, v ktorých sa doména a kodominium zhodujú.

Automorfizmy

Tento druh lineárnych transformácií sú bijektívne endomorfizmy.

Špeciálne lineárne transformácie

Lineárny operátor

Lineárna transformácia T: V → V, ktorá prechádza z vektorového priestoru do rovnakého vektorového priestoru, sa nazýva Lineárny operátor.

Nulová transformácia

Vyššie uvedená nulová transformácia je dôležitá na nájdenie jadra lineárnej transformácie:

Môže vám slúžiť: Tetradecagon

T: v → w tak, že t (vložka) = 0 Za každého vložka.

Transformácia identity

T: V → V tak, že t (vložka) = vložka  Za každého vložka.

Transformácia definovaná maticou

T: v → w tak, že t (vložka) = Avložka, kde A je matica a vložka Je to vektor stĺpca.

Lemovacia zábava

Lineárne funkcie typu y = mx sú lineárne transformácie. Zoberme si napríklad y = 3x a zistite, či spĺňa dve podmienky začiatku, testovanie s dvoma hodnotami a a b akýmkoľvek:

f (a+b) = 3 (a+b) = 3a+3b = f (a)+f (b)

f (ka) = 3 (ka) = k⋅ (3a) = k⋅f (a)

V skutočnosti je to lineárna transformácia.

Žiadosti

Lineárne transformácie majú matematické aplikácie, napríklad:

-Koordinované nápravy.

-V riešení systémov lineárnych diferenciálnych rovníc.

-Problémy s vlastnou hodnotou a autovstvom.

A majú tiež aplikácie v iných oblastiach vedy, napríklad v mechanike, kvantovej mechanike a ekonomike,.

Príklady lineárnych transformácií

Príklad 1

V mnohých mechanických problémoch musíme nájsť projekciu vektora vložka patriace do priestoru, v určitej rovine. Tento vektor vložka môže predstavovať napríklad silu.

Predpokladajme, že chcete premietať vektor vložka = Na rovine XY. Môžeme definovať lineárnu transformáciu danú nasledujúcou maticou:

Keď ho aplikujeme na vektor vložka Dostávame vektor, ktorého komponent Z je zrušený. Geometricky je zastúpený, s projekciou vložka Na rovine XY ako červený vektor s dvoma komponentmi.

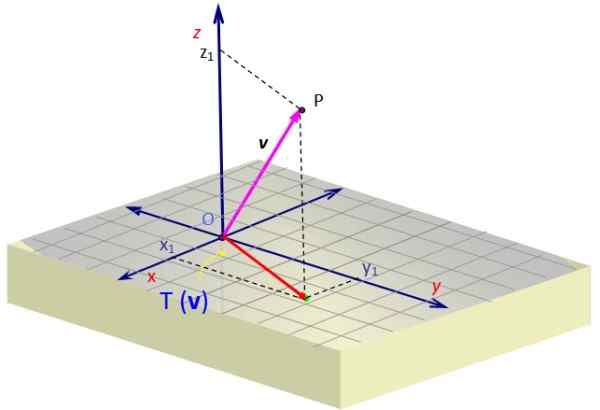Obrázok 2. Projekcia vektora vo vesmíre v rovine, ktorá sa získa lineárnou transformáciou. Zdroj: f. Zapata.

Príklad 2

Predpokladajme, že máte továreň, ktorá vyrába tri typy hračiek: C1, C2 a C3, pre ktoré na druhej strane potrebujete tri typy kusov v určitých množstvách na výrobu každého typu vozíka:

-Osi alebo kus

-Kolesá alebo kus B

-Podvozok alebo kus C

Pre každý typ vozíka je počet kusov iný, pretože modely sú rôzne. Môžeme sa ubytovať sumy v matici 3 × 3, v ktorej sú stĺpy v čele s typom vozíka a rady zodpovedajú množstvu kusov potrebných na vypracovanie každého modelu.

Toto je príklad transformácie danej maticou, ktorá by bola taká:

Ak továreň dostane určitú objednávku, ktorá pozostáva z X množstvo C1, a  C2 a z Z C3, koľko kusov A, B a C musí mať k dispozícii na zostavenie objednávkových vozíkov?

Môže vám slúžiť: Aké sú algebraické výrazy a ktoré sú najčastejšie?

Musíme nájsť lineárnu transformáciu t (x) tak, že:

Získať vektor a:

To nám poskytne množstvo častí, ktoré musíme mať pri likvidácii. V roku vyriešené 2 vyhodnotíme efektívnosť lineárnych transformácií, aby sme našli množstvo častí potrebných na splnenie určitej objednávky.

Vyriešené cvičenia

- Cvičenie 1

Skontrolujte, či nasledujúca transformácia t: r² → R² Je lineárna:

Riešenie

Aby ste to dosiahli, musíte sa ubezpečiť, že transformácia spĺňa dve podmienky opísané na začiatku, najskôr sčítanie a potom produkt skalára pre vektor. Takže musíte vziať dva vektory vložka a  alebo patriaci k r², Písanie ich notácie Matrix alebo zadanie komponentov.

Tieto vektory sú:

vložka = x₁, a₁

alebo = x₂, a₂

Prvá podmienka

-Pamätajte si, že vektory sú pridané komponentom komponentu, je potrebné overiť, že:

T (vložka+alebo) = T (vložka) + T (alebo)

T (vložka+alebo) = T (x₁+ X₂ ; a₁ + a₂)

Odtiaľ sa získava:

T (x₁+ X₂ ; a₁ + a₂) = (x₁+ X₂; 0)

-Na druhej strane pri aplikácii transformácie na každý vektor osobitne:

T (x₁,a₁) + T (x₂,a₂) = (x₁,0) + (x₂,0)

Pridaním výsledných vektorov sa efektívne získava:

W = (X₁+ X₂; 0)

Pretože oba výsledky sú identické, je splnená prvá podmienka.

Druhá podmienka

Teraz sa chystáme overiť, že vynásobením skricom C môže ísť z transformácie:

T (cvložka) = c⋅t (vložka)

Sean:

vložka = x₁, a₁

c.vložka = C⋅x₁, Clek₁

Tak:

T (cvložka) = T (c⋅x₁, Clek₁ ) = (C⋅x₁ , 0)

Ale vieme, že z predchádzajúceho kroku T (vložka) = T (x₁, a₁ ) = (X₁ , 0).

Takže obidva výrazy sú identické, splní sa aj druhá podmienka a transformácia je lineárna.

- Cvičenie 2

Továreň na hračkársky vozík zostavuje tri modely vozidla: C1, C2 a C3, pre ktoré potrebujete kúsky A, B a C, ktoré sú nápravami, kolesami a podvozkom. Požadované sumy sú v nasledujúcej tabuľke:

Továreň bola požiadaná o prípravu 12 modelov C1, 22 C2 a 16 C3. Koľko kusov A, B a C sa vyžaduje na dokončenie objednávky?

Riešenie

Použije sa lineárna transformácia t (x) = y, ktorej výsledkom je produkt medzi matkami:

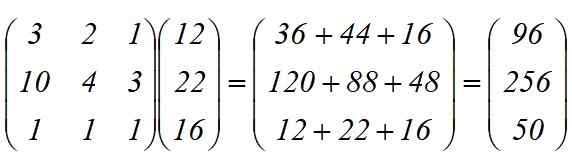
Celkovo sú potrebné:

-96 osí

-256 kolies

-50 podvozku.

Odkazy

1. Algebra a analytická geometria. Jadro. Klasifikácia lineárnych transformácií. Získané z: AGA.frba.Utn.Edu.ar.
2. Grossman, s. 2012. Lineárna algebra. 7. Vydanie. McGraw Hill.
3. Gutiérrez, e. 2014. Lineárna algebra a jej aplikácie. Redakčná skupina Patria.
4. Larson, R. 2016. Základy lineárnej algebry. 6. Vydanie. Učenie sa.
5. Wikipedia. Lineárne aplikácie. Obnovené z: je.Wikipedia.orgán.