Vertikálne vzorce streľby, rovnice, príklady

On vertikálna streľba Je to hnutie, ktoré sa odohráva v rámci pôsobenia poľa síl, bežne gravitácie, ktorý je schopný stúpať alebo zostupovať. Je tiež známy pod názvom Vertikálne spustenie.

Najpôsobivejší príklad je vyhodený (alebo dole, ak je uprednostňovaný) loptu s rukou, áno, uistite sa, že to urobíte vertikálne. Pohyb opovrhujúceho vzduchu, pohyb, ktorý sleduje loptu, perfektne zapadá do rovnomerne rozmanitého modelu priamočiary (MRUV).

postava 1. Hovoriť lopta vertikálne hore je dobrým príkladom vertikálneho výstrelu. Zdroj: pexels.

Vertikálna streľba je široko študovaným pohybom v úvodných kurzoch fyziky, pretože ide o vzorku Pohyb v dimenzii, Veľmi jednoduchý a užitočný model.

Tento model sa dá použiť nielen na štúdium kinematiky objektov pod pôsobením gravitácie, ale, ako bude vidieť neskôr, opisuje pohyb častíc uprostred jednotného elektrického poľa.

[TOC]

Vzorce a rovnice

Prvá vec, ktorá je potrebná, je súradnicový systém na označenie pôvodu a označenie písmenom, ktorý je v prípade vertikálnych pohybov písmeno “a„.

Potom je vybraný pozitívny zmysel +a, čo je zvyčajne hore a význam -a to sa zvyčajne stiahne (pozri obrázok 2). To všetko, pokiaľ tento problém nevyrieši inak, pretože inou možnosťou je brať ako pozitívny smer pohybu, nech je to čokoľvek.

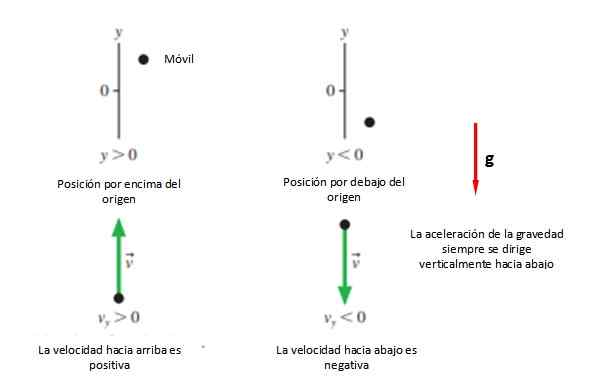Obrázok 2. Zvyčajný konvent Značkov vo vertikálnom výstrele. Zdroj: f. Zapata.

V každom prípade sa odporúča, aby sa pôvod zhodoval s bodom spustenia a_ani, Pretože rovnice sú zjednodušené, hoci je možné zaujať akúkoľvek polohu, ktorá sa má na začiatku štúdia pohybu.

Môže vám slúžiť: Druhá rovnovážna podmienka: Vysvetlenie, príklady, cvičenia

Vertikálne streľba

Akonáhle sú koordinačný systém a pôvod, ideme do rovníc. Všeobecné, ktoré opisujú pohyb, sú:

-Počiatočná rýchlosť vložka_ani

-Zrýchlenie do

-Rýchlosť vložka

-Počiatočná pozícia X_ani

-Pozícia X

-Posunutie DX

-Čas tón

Všetky okrem času sú vektory, ale keďže ide o jednorozmerný pohyb s určitým smerom, na ktorom záleží, potom používa príznaky + alebo - na poukázanie na miesto, kde je nasmerovaná príslušná veľkosť. V prípade vertikálneho streľby vždy gravitácia klesá a, pokiaľ nie je uvedené inak, je udelené znamenie -.

Potom existujú rovnice prispôsobené pre vertikálne snímanie a nahradia sa “X„od“a„A“do„od“g„. Okrem toho značka (-) zodpovedajúce gravitácii nasmerovanej nadol:

1) Poloha: y = y_ani + vložka_ani.T - ½ g.tón²

2) Rýchlosť: v = v_ani - g.tón

3) Rýchlosť v závislosti od posunu δa: vložka² = v_ani² - 2.g. Δa

Príklady

Potom sú k dispozícii príklady aplikácií na vertikálne snímanie. Vo svojom rozlíšení sa musí zohľadniť nasledujúce:

-„g„Má konštantnú hodnotu, ktorá je v priemere 9,8 m/s² alebo približne 10 m/s² Ak je uprednostňovaný na uľahčenie výpočtov, ak sa nevyžaduje príliš presnosť.

-Kedy vložka_ani V poriadku 0, Tieto rovnice sa redukujú na rovnosti voľný pád.

-Ak je spustenie hore, objekt musí mať počiatočnú rýchlosť, ktorá vám umožní pohybovať sa. Akonáhle je v pohybe, objekt dosiahne maximálnu výšku, ktorá bude závisieť od toho, aká veľká je počiatočná rýchlosť. Samozrejme vo väčšej výške mobil trávi viac času vo vzduchu.

-Objekt sa vracia do východiskového bodu s rovnakou rýchlosťou, akou bol spustený, ale rýchlosť je nasmerovaná nadol.

-Pre vertikálne spustenie, čím vyššia je počiatočná rýchlosť, tým skôr sa objekt dostane na zem. Tu je prevezená vzdialenosť pevná podľa vybranej výšky na spustenie.

Môže vám slúžiť: čo je relatívna a absolútna drsnosť?

-Pri zvislej výstrele sa čas, ktorý trvá mobilný telefón, dosiahne maximálnu výšku v = 0 V rovnici 2) predchádzajúcej časti. To je maximálny čas tón_Maximálny:

0 = v_ani - g . tón_Maximálny ⇒ tón_Maximálny = v_ani /g

-Ten maximálna výška a_Maximálny Vymaže z rovnice 3) aj predchádzajúcej časti v = 0:

0 = v_ani² - 2.g. Δy ⇒ 0 = v_ani² - 2.g. (a_Maximálny - a_ani) ⇒ a_Maximálny = y_ani  + vložka_ani² / 2 g

Jo a_ani = 0, Je to redukované na:

a_Maximálny = v_ani² / 2 g

Vyriešený príklad 1

Lopta s V sa hodí zvisle nahor_ani = 14 m/s, z vrcholu 18 m vysokej budovy. Lopta môže nasledovať po prúde k chodníku. Vypočítať:

a) maximálna výška dosiahnutá loptou vzhľadom na zem.

b) čas vo vzduchu (čas letu).

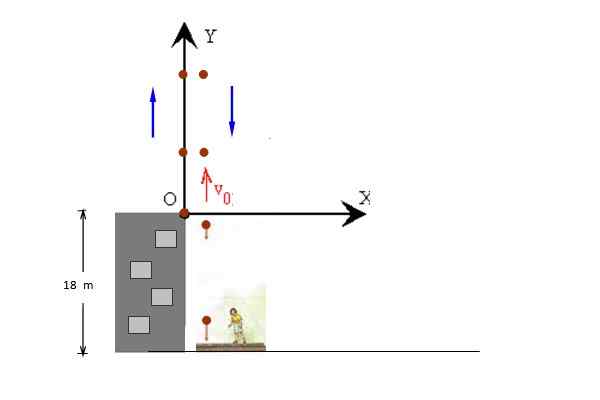Obrázok 3. Lopta je vyhodená zvisle zo strechy budovy. Zdroj: f. Zapata.

Riešenie

Na obrázku sa pohyby stúpania a spúšťania lopty javia osobitne kvôli prehľadnosti, ale obidva sa vyskytujú v rovnakej línii. Počiatočná poloha sa prijíma na y = 0, takže konečná poloha je y = - 18 m.

a) maximálne meranie merané zo strechy budovy je a_Maximálny = v_ani² / 2 g A z vyhlásenia sa znie, že počiatočná rýchlosť je +14 m/s, potom:

a_Maximálny = (14 m/s)² / 2 x 9.8 m/s² = 10 m (Týkajúce sa strechy)

H_Maximálny = 10 m + 18 m = 28 m (Týkajúce sa chodníka).

b) nájsť Celkový čas ani čas letu Trvá vo vzduchu, lopta sa použije rovnica y = y_ani + vložka_ani.T - ½ g.tón², S nasledujúcimi hodnotami a znakmi:

y = - 18 m

a_ani = 0 m

vložka_ani = +14 m/s

Výmena:

- 18 = 14.T - ½ 9.8 .tón²

- 4.9 t²+14.T + 18 = 0 

4.9 t²-14.T - 18 = 0

Je to druhá rovnica, ktorá sa ľahko vyrieši pomocou vedeckej kalkulačky alebo pomocou rozlíšenia. Riešenia sú: 3.82 a -0.96. Negatívne riešenie sa vyradí, pretože čas nemá fyzický význam.

Môže vám slúžiť: teplo: vzorce a jednotky, charakteristiky, ako sa meria, príklady

Čas lietania lopty je 3.82 sekúnd.

Vyriešený príklad 2

Pozitívne načítaná častica s Q = +1.2 milicoulomby (MC) a hmotnosť m = 2.3 x 10 ^-10 Kg Premieta sa vertikálne nahor, počínajúc z polohy znázornenej na obrázku a počiatočnou rýchlosťou vložka_ani = 30 km/s.

Medzi naloženými doskami je elektrické pole A jednotný, nasmerovaný vertikálne nadol a veľkosť 780 n/c. Ak je vzdialenosť medzi doskami 18 cm, zrazí sa častice s hornou doskou? Opovrhujte gravitačnú príťažlivosť na častice, pretože je extrémne ľahký.

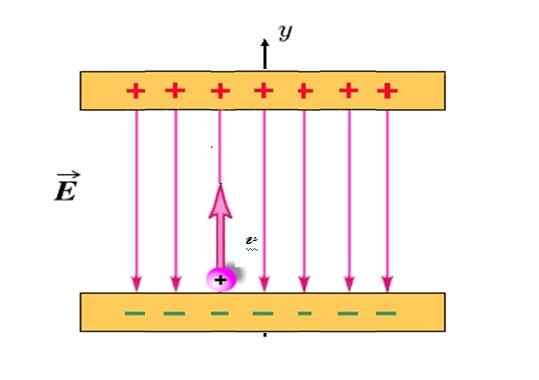Obrázok 4. Pozitívne zaťažovacie častice sa pohybujú podobne ako guľa vyhodená zvisle nahor, keď je ponorená do elektrického poľa obrázku. Zdroj: upravené podľa f. Wikimedia Commons Shoe.

Riešenie

V tomto probléme elektrické pole A je ten, ktorý vytvára silu F a následné zrýchlenie. Častica, ktorá je pozitívne načítaná, je vždy priťahovaná na spodnú dosku, avšak keď sa premieta vertikálne nahor, dosiahne maximálnu výšku a potom sa vráti na dolnú dosku, ako je napríklad guľa predchádzajúcich príkladov.

Podľa definície elektrického poľa:

E = f/q = m.A /Q ⇒ A = Q.E / m

Pred výmenou hodnôt je potrebné použiť túto rovnocennosť:

1 mc = 1 x 10^-3 C

S tým je zrýchlenie:

A = 1.2 x 10^-3 X 780 /2.3 x 10 ^-10pani² = 4.07 x 10⁹ pani²

Pre maximálnu výšku sa používa vzorec predchádzajúcej sekcie, ale namiesto použitia “g„Táto hodnota zrýchlenia sa používa:

a_Maximálny = v_ani² / 2a = (30.000 m/s)²/2 x 4.07 x 10⁹ pani² = 0.11 m = 11 cm

Nezrážajte sa s hornou doskou, pretože je 18 cm od východiskového bodu a častice, akonáhle zdvihne 11 cm.

https: // youtu.Be/kt08ntudzwq

Odkazy

1. Kirkpatrick, L. 2007. Fyzika: pohľad na svet. 6^{ubytovať sa} Skrátene vydanie. Učenie sa. 23 - 27.
2. Rex, a. 2011. Základy fyziky. Pearson. 33 - 36
3. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14^th. Edimatizovať. Zväzok 1. 50 - 53.
4. Serway, r., Vulle, C. 2011. Základy fyziky. 9^nat Edimatizovať. Učenie sa. 43 - 55.
5. Wilson, J. 2011. Fyzika 10. Pearson Vzdelanie. 133 - 149.