Príkladové charakteristiky parabolických záberov, vzorce, rovnice, príklady

On Obchodný parabolický výstrel Je to konkrétny prípad pohybu voľného pádu, v ktorom počiatočná rýchlosť projektilu tvorí určitý uhol s horizontálnym, čo vedie k parabolickej ceste.

Voľný pád je prípad pohybu s konštantným zrýchlením, v ktorom je zrýchlenie gravitácie, ktorá vždy smeruje vertikálne nadol a má veľkosť 9,8 m/s^2. Nezávisí to od cesta projektilu, ako demonštroval Galileo Galilei v roku 1604.

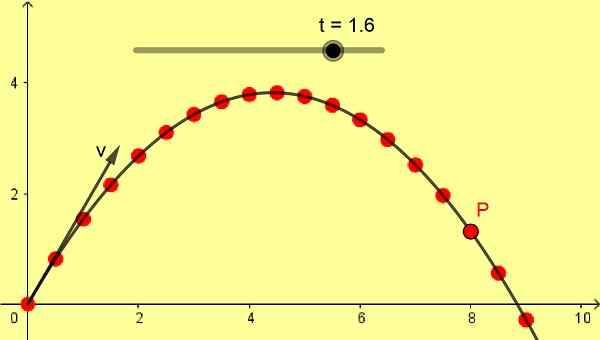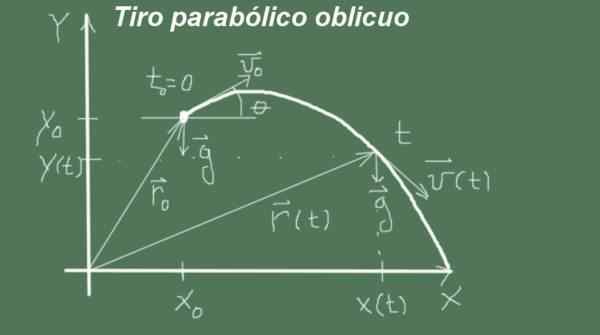
postava 1. Obchodný parabolický výstrel. (Vlastné rozpracovanie)

Ak je počiatočná rýchlosť projektilu vertikálny, voľný pád má rovnú a vertikálnu trajektóriu, ale ak je počiatočná rýchlosť šikmá, trajektória voľného pádu je parabolická krivka, tiež preukázaná Galileom.

Príklady parabolického pohybu sú trajektória, ktorá sleduje baseball, strela vystrelená delom a vodným prúdom, ktorý vychádza z hadice.

Obrázok 1 zobrazuje šikmý parabolický záber 10 m/s s uhlom 60 °. Stupnica je v metroch a postupné pozície P sa prijímajú s rozdielom 0,1 s od počiatočného momentu 0 sekúnd.

[TOC]

Vzorce

Pohyb častíc je úplne opísaný, ak je jeho poloha známa, jeho rýchlosť a zrýchlenie ako funkcia času.

Parabolický pohyb vyplývajúci z šikmého výstrelu je superpozícia horizontálneho pohybu pri konštantnej rýchlosti a vertikálny pohyb s konštantným zrýchlením rovnajúcim sa zrýchleniu gravitácie.

Vzorce, ktoré sa vzťahujú na šikmú parabolickú strelu, sú tie, ktoré zodpovedajú pohybu s konštantným zrýchlením a = g, Všimnite si, že tučný program sa použil na označenie, že zrýchlenie je vektorová suma.

Môže vám slúžiť: prírodné satelity

Poloha a rýchlosť 

V konštantnom pohybe zrýchlenia matematicky závisí od času kvadratickým spôsobom.

Ak označíme r(T) Pozícia do času tón, rani Počiatočná okamžitá poloha, vložkaani Počiatočná rýchlosť, g zrýchlenie a t = 0 Ako počiatočný moment vzorec, ktorý dáva polohu pre každý okamih času tón je:

r(t) = r_ani + vložka_ani T + ½ g tón²

Tučný výraz v predchádzajúcom výraze naznačuje, že ide o vektorovú rovnicu.

Rýchlosť ako funkcia času sa získava z užívania derivátu vzhľadom na T polohy a výsledkom je:

vložka(t) = vložka_ani + g tón

A na získanie zrýchlenia ako funkcia času, rýchlosť odvodená tón výsledné:

do(t) = g

Ak nie je k dispozícii čas, existuje vzťah medzi rýchlosťou a polohou, ktorý je daný:

vložka² = vani² - 2 g (a - ja)

Rovnicia

Ďalej nájdeme rovnice, ktoré sa vzťahujú na šikmý parabolický záber v karteziánskej podobe.

Obrázok 2. Premenné a parametre šikmého parabolického výstrelu. (Vlastné rozpracovanie)

Momentálne sa začína pohyb t = 0 S počiatočnou polohou (Xo, ja) a rýchlosť veľkosti vložkaani a uhol θ, To znamená, že počiatočný vektor rýchlosti je (vani cosθ, vani Senθ). Pohyb prechádza zrýchlením 

g = (0, -g).

Parametrické rovnice

Ak sa použije vektorový vzorec, ktorý poskytuje polohu ako funkciu času, a komponenty sú zoskupené a vyrovnané, získajú sa rovnice dané súradnicami polohy do ľubovoľného času t.

x (t) = x_ani + vložka_vôl tón 

a (t) = y_ani + vložka_Odvoz t -½ g t²

Podobne sú rovnice pre rýchlostné komponenty ako časová funkcia.

Môže vám slúžiť: Normálne úsilie: z čoho sa skladá, ako sa vypočíta, príklady

vložka_X(t) = v_vôl

vložka_a(t) = v_Odvoz - g t 

Kde: vložka_vôl = vani cosθ; vložka_Odvoz = vani Senátor

Rovnica trajektórie

y = a x^2 + b x + c

A = -g/(2 Vvôl^2)

B = (vOdvoz/vvôl + g xani/vvôl^2)

C = (aani - vložkaOdvoz Xani / vvôl)

Príklady 

Príklad 1

Odpovedaj na nasledujúce otázky:

a) Prečo v problémoch s parabolickým streľbou zvyčajne opovrhuje účinok trenia vzduchom?

b) robí tvar objektu v parabolickom zábere?

Odpovedať

a) Aby bol pohyb projektilu parabolický, je dôležité, aby si sila vzduchu bola oveľa nižšia ako hmotnosť, ktorý sa spustí. 

Ak je vyhodená korková guľa alebo nejaký svetelný materiál, trecia sila je porovnateľná s hmotnosťou a jej trajektória sa nemôže priblížiť k parabole.

Naopak, ak je to ťažký predmet ako kameň, trecia sila je zanedbateľná v porovnaní s hmotnosťou kameňa a jeho trajektóriu sa blíži k parabole.

b) Relevantný tvar, ktorý sa spustí, je tiež relevantný. Ak sa spustí plata lietadla vo forme Avionncito, jej pohyb nebude voľný alebo parabolický, pretože forma uprednostňuje odpor vzduchu.

Na druhej strane, ak je ten istý list papiera kompaktný vo forme gule, výsledný pohyb je veľmi podobný parabole.

Príklad 2

Z horizontálnej podlahy sa spustí projektil rýchlo 10 m/s a 60 ° uhol. Toto sú rovnaké údaje, s ktorými bol vyvinutý obrázok 1. S týmito údajmi nájdem:

a) Moment, v ktorom dosahuje maximálnu výšku.

Môže vám slúžiť: Aké sú tepelné vlastnosti a čo sú? (S príkladmi)

b) maximálna výška.

c) Rýchlosť v maximálnej výške.

d) poloha a rýchlosť o 1,6 s.

e) V okamihu, keď opäť hrá pôdu.

f) horizontálny rozsah.

Riešenie do)

Vertikálna rýchlosť v závislosti od času je

vložka_a(t) = v_Odvoz - G t = v_ani Senθ - G T = 10 sen60 ° - 9.8 t = 8.66 - 9.8 t 

V čase dosiahnutia maximálnej výšky je zvislá rýchlosť na chvíľu nula.   

8.66 - 9.8 t = 0 ⇒ t = 0.88 s.

Riešenie b)

Maximálna výška je daná súradnicou a Pre okamih, keď sa dosiahne táto výška:

a (0.88s) = Jo budem t -½ g t^2 = 0 + 8.66*0.88-½ 9.8 0.88^2 = 

3.83 m

Preto maximálna výška je 3.83 m.

Riešenie c)

Rýchlosť v maximálnej výške je vodorovná:

vložka_X(t) = v_vôl = v_ani cosθ = 10 cos60 ° = 5 m/s 

D) Riešenie

Pozícia v 1.6 s je:

X (1.6) = 5*1,6 = 8,0 m

a (1.6) = 8.66*1.6 -½ 9.8 1.62 = 1.31 m

Riešenie e)

Keď sa súradnica dotkne a je zrušená, potom:

a (t) = 8.66*t -½ 9.8 t2 = 0 ⇒ t = 1,77 s

Riešenie f)

Horizontálny rozsah je súradnicou X v okamihu, keď hrá pôdu:

X (1.77) = 5*1,77 = 8,85 m

Príklad 3

Nájdite rovnicu trajektórie s údajmi o príklade 2.

Riešenie 

Parametrická rovnica trajektórie je:

x (t) = 5*t

a (t) = 8.66*t -½ 9.8 t^2

A karteziánska rovnica sa získa zúčtovaním T prvého a nahradením druhého

y = 8.66*(x/5) -½ 9.8 (x/5)^2

Zjednodušenie:

y = 1,73 x - 0,20 x^2 

Odkazy

1. P. P. Teodorescu (2007). „Kinematika“. Mechanické systémy, klasické modely: mechanika častíc. Prubár.
2. Resnick, Halliday a Krane (2002). Fyzika Zväzok 1. CECSA, Mexiko.
3. Thomas Wallace Wright (1896). Prvky mechaniky vrátane kinematiky, kinetiky a statiky. E a fn spona.
4. Wikipedia. Parabolické hnutie. Zotavené z es.Wikipedia.orgán.
5. Wikipedia. Projektil.Získaný z.Wikipedia.orgán.