Charakteristiky parabolického záberu, vzorce a rovnice, príklady

On parabolický výstrel Skladá sa z hádzania objektu alebo projektilu s určitým uhlom a nechať ho pohybovať sa pod konaním gravitácie. Ak sa nezohľadňuje odpor vzduchu, objekt, bez ohľadu na jeho povahu, bude nasledovať trajektóriu vo forme paraboly.

Je to každodenný pohyb, pretože medzi najobľúbenejšie športy sú tie, v ktorých sú lopty alebo gule vyhodené ručne, s nohou alebo s nástrojom, ako je napríklad raketa alebo netopier.

postava 1. Vodný prúd z okrasného zdroja sleduje parabolickú trajektóriu. Zdroj: Wikimedia Commons. Zátonyi Sandor (ifj.), Fizped/CC By-SA (https: // creativeCommons.Org/licencie/By-SA/3.0)

Na štúdium je parabolický výstrel rozdelený na dva prekrývajúce sa pohyby: jeden horizontálny bez zrýchlenia a druhý vertikálny s konštantným zrýchlením nadol, čo je gravitácia. Oba pohyby majú počiatočnú rýchlosť.

Povedzme, že horizontálny pohyb trvá. Každý z týchto pohybov je nezávislý od druhého.

Vzhľadom na skutočnosť, že stanovenie pozície projektilu je hlavnými cieľmi, je potrebné zvoliť príslušný referenčný systém. Detaily budú nasledujúce.

[TOC]

Vzorce a rovnice parabolického výstrelu

Predpokladajme, že objekt je hodený s uhlom a vzhľadom na vodorovnú a počiatočnú rýchlosť vložka_ani Ako je znázornené na obrázku nižšie vľavo. Parabolický výstrel je pohyb, ktorý sa odohráva v lietadle Xy A v takom prípade sa počiatočné rozkladá takto rozkladá:

vložka_vôl = v_ani cos α

vložka_Odvoz = v_ani hriech α

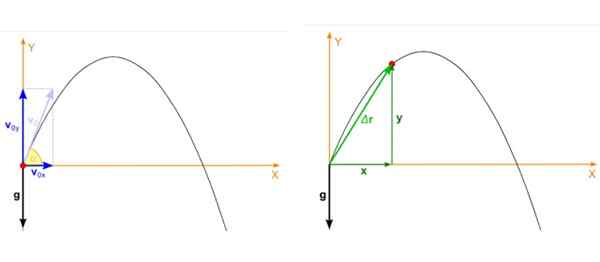Obrázok 2. Vľavo počiatočná rýchlosť projektilu a doprava polohu v akomkoľvek okamihu spustenia. Zdroj: Wikimedia Commons. Zátonyi Sandor, (ifj.) Fizped/CC By-SA (https: // creativeCommons.Org/licencie/By-SA/3.0).

Poloha projektilu, ktorá je červeným bodom na obrázku 2, správny obraz, má tiež dve komponenty, ktoré závisia od času, jedna v X A druhý v a. Pozícia je vektor, ktorý sa označuje ako r a jeho jednotky sú dĺžky.

Môže vám slúžiť: izoméria

Na obrázku sa počiatočná poloha projektilu zhoduje s pôvodom súradníckeho systému, teda x_ani = 0 a_ani = 0. Nie je to tak vždy, pôvod je možné zvoliť kdekoľvek, ale táto voľba veľa zjednodušuje výpočty veľa.

Pokiaľ ide o dva pohyby v X a Y, sú to:

-X (t): Je to rovnomerný priamy pohyb.

-a (t): zodpovedá rovnomerne zrýchlenému priamočiarovému pohybu s G = 9.8 m/s² a smerujúce vertikálne nadol.

V matematickej podobe:

x (t) = v_ani cos α.tón

a (t) = v_ani .hriech α.T - ½g.tón²

Vektor polohy zostáva:

r (t) = [v_ani cos α.t]Jo + [v_ani .hriech α.T - ½g.tón²] J

V týchto rovniciach si pozorný čitateľ všimne, že znamenie mínus je spôsobené skutočnosťou, že závažnosť poukazuje na zem, zmysel zvolený ako negatívny, zatiaľ čo nahor sa považuje za pozitívny.

Pretože rýchlosť je prvá odvodená z polohy, stačí odvodiť r t) Pokiaľ ide o čas a získanie:

vložka (t) = v_ani cos α Jo + (v_ani .hriech α - Gt) J

Nakoniec je zrýchlenie vyjadrené vektorovo ako:

do (t) = -g J

- Trajektória, maximálna výška, maximálny čas a horizontálny dosah

Trajektória

Ak chcete nájsť explicitnú rovnicu trajektórie, ktorá je krivkou y (x), musíte eliminovať časový parameter, vyčistiť v rovnici pre x (t) a nahradiť v y (t). Zjednodušenie je trochu namáhavé, ale konečne sa získa:

Maximálna výška

Maximálna výška sa vyskytuje, keď vložka_a = 0. Vedieť, že existuje ďalší vzťah medzi polohou a štvorcom rýchlosti:

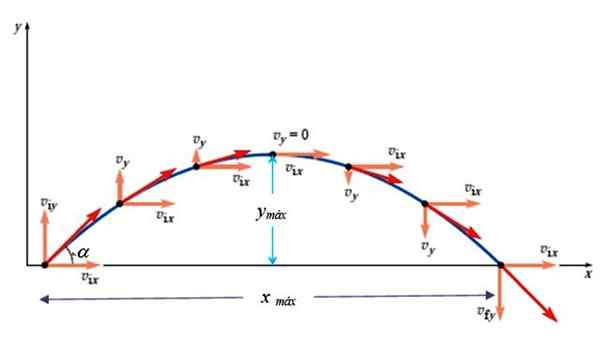Obrázok 3. Rýchlosť v parabolickom výstrele. Zdroj: Giambattista, a. Fyzika.

vložka_a² = v_Odvoz ²- 2GY

Robí vložka_a = 0 Práve keď dosiahne maximálnu výšku:

0 = v_Odvoz ²- 2 g.a_maximálny → a_maximálny = v_Odvoz ²/2 g

S:

Môže vám slúžiť: Centripetálne zrýchlenie: Definícia, vzorce, výpočet, cvičenia

vložka_Odvoz = v_ani Sena

Maximálny čas

Maximálny čas je čas, ktorý objekt potrebuje na dosiahnutie a_maximálny. Na jeho výpočet sa používa:

vložka_a = v_ani .hriech α - Gt

S vedomím, že vložka_a Sa to robí 0, kedy t = t_maximálny, výsledok:

vložka_ani .hriech α - g.tón_maximálny = 0

tón_maximálny = v_Odvoz /g

Maximálny horizontálny rozsah a čas letu

Rozsah je veľmi dôležitý, pretože naznačuje, kde objekt klesne. Takže budeme vedieť, či to dáva biele. Aby sme to našli, potrebujeme čas letu, celkový čas alebo t_vložka.

Z predchádzajúcej ilustrácie je ľahké vyvodiť k záveru tón_vložka = 2.tón_maximálny. Pozornosť však platí iba vtedy, ak je uvedenie na trh na úrovni, to znamená, že výška východiskového bodu je rovnaká ako výška príchodu. Inak čas rieši rovnicu druhého stupňa, ktorá je výsledkom výmeny konečnej polohy a_Konečný:

a_Konečný = v_ani .hriech α.tón_vložka - ½g.tón_vložka²

V každom prípade je maximálny horizontálny rozsah:

X_maximálny = v_vôl. tón_vložka

Príklady parabolického streľby

Parabolický výstrel je súčasťou pohybu ľudí a zvierat. Taktiež takmer všetkých športov a hier, do ktorých zasahuje gravitácia. Napríklad:

Parabolické natáčanie v ľudských aktivitách

-Kameň hodený katapultom.

-Cieľ brankára.

-Lopta, ktorá hodí džbán.

-Šípka, ktorá vychádza z oblúka.

-Všetky druhy skokov

-Hodiť kameň.

-Akákoľvek hádzacia zbraň.

Obrázok 4. Kameň hodený katapultom a patey loptičkou v cieľovej skrinke sú príklady parabolických záberov. Zdroj: Wikimedia Commons.

Parabolický výstrel v prírode

-Voda plíži z prírodných alebo umelých trysiek, ako je zdroj zdrojov.

-Kamene a láva pučanie zo sopky.

-Lopta, ktorá odráža chodník alebo kameň, ktorý to robí na vode.

-Všetky druhy zvierat, ktoré skočia: klokany, delfíny, gazely, mačky, žaby, králiky alebo hmyz, aby sme spomenuli niekoľko.

Môže vám slúžiť: Mechanical Power: Čo je, aplikácie, príkladyObrázok 5. Impala je schopná skočiť na 3 m. Zdroj: Wikimedia Commons. Arturo de Frias Marques/CC By-S (https: // creativeCommons.Org/licencie/By-SA/3.0).

Cvičenie

Kobylky tvoriaci uhol 55 ° s vodorovným a pristáva na 0.O 80 metrov neskôr. Nájsť:

a) dosiahnutá maximálna výška.

b) Keby som skočil s rovnakou počiatočnou rýchlosťou, ale vytvoril by som uhol 45 °, vyšlo by to vyššie?

c) Čo sa dá povedať o maximálnom horizontálnom dosahu tohto uhla?

Roztok

Ak údaje poskytnuté problémom neobsahujú počiatočnú rýchlosť v_ani Výpočty sú o niečo namáhavejšie, ale zo známych rovníc možno odvodiť nový výraz. Začať z:

X_maximálny = v_vôl . tón_let = v_ani.cos α. tón_vložka

Keď pristane neskôr, výška je opäť 0, potom:

vložka_ani .hriech α.tón_vložka - ½g.tón_vložka²= 0

Ako tón_vložka Je to spoločný faktor, je zjednodušený:

vložka_ani .hriech α - ½g.tón_vložka= 0

Môžeme vyčistiť t_vložka Z prvej rovnice:

tón_vložka = x_maximálny / v_ani.cos α

A vymeňte v druhom:

vložka_ani .hriech α - (½g.X_maximálny / v_ani.cos α) = 0

Vynásobením všetkých výrazov vložka_ani.cos αVýraz sa nemení a menovateľ zmizne:

(v_ani .hriech α.) (v_ani.cos α) - ½g.X_maximálny = 0

vložka_ani² hriech α. cos α = ½g.X_maximálny

Už sa dá vyčistiť v_ani Alebo tiež vymeňte nasledujúcu identitu:

Sen 2a = 2 sen α. cos α → V_ani² Sen 2α = g.X_maximálny

Je vypočítaný vložka_ani²:

vložka_ani² = g.X_maximálny / Sen 2a = (9.8 x 0.8 / sen 110) m²/s² = 8.34 m²/s²

A nakoniec maximálna výška:

a_maximálny= v_Odvoz ²/2G = (8.34 x sen² 55)/(2 x 9.8) m = 0.286 m = 28.6 cm

Riešenie B

Lobster dokáže udržať rovnakú vodorovnú rýchlosť, ale keď uhol klesá:

a_maximálny= v_Odvoz ²/2G = (8.34 x sen² 45)/(2 x 9.8) m = 0.213 m = 21.3 cm

Dosahuje menšiu výšku.

Riešenie c

Maximálny horizontálny rozsah je:

X_maximálny = v_ani² Sen 2a / g

Keď sa uhol líši, zmení sa aj horizontálny rozsah:

X_maximálny = 8.3. 4 Sen 90 / 9.8  m = 0.851 m = 85.1 cm

Skok je teraz dlhší. Čitateľ môže overiť, či je maximálny pre uhol 45 ° potom:

sin 2a = sin 90 = 1.

Odkazy

1. Figueroa, D. 2005. Séria: Fyzika pre vedu a inžinierstvo. Zväzok 1. Kinematika. Editoval Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fyzika. Druhé vydanie. McGraw Hill.
3. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6. Ed Prentice Hall.
4. Resnick, r. 1999. Fyzický. Zvuk. 1. 3. vydanie. v španielčine. Kontinentálna redakčná spoločnosť s.Do. c.Vložka.
5. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 1.