Typy funkcií a ich grafy

- 5032
- 409
- Blažej Hrmo
Sú rozmanité Typy funkcií ktoré sa používajú na modelovanie problémov v odvetviach vedomostí, ako sú prírodné vedy, administratíva, hospodárstvo a sociálne vedy. Matematicky povedané, funkcia je vzťah medzi dvoma alebo viacerými premennými.
Niektoré objekty alebo množstvá mnohokrát navzájom súvisia. Tieto sumy sú reprezentované premennými. Napríklad existujú dve súvisiace premenné, ktoré patria do dvoch súprav A a B, nie nevyhnutne číselné, hoci väčšinou sú-.
Aby bol tento vzťah považovaný za funkciu, musí splniť dve podmienky: prvé je, že všetky prvky štartovacej súbory sa zúčastnia, a druhý, že každý prvok uvedeného súboru súvisí iba s jedným z prvkov set b.
Premenné sa zvyčajne nazývajú písmenami X a a, s X ako nezávislá premenná a a ako závislá premenná. Prirodzene, môžu byť zavolané iným spôsobom a vyberú názov premennej v súlade s veľkosťou, ktorú predstavuje.
Vzťah medzi nimi je označený listom F -alebo ďalšie písmeno abecedy a je znázornené niekoľkými spôsobmi, ako napríklad súbor usporiadaných párov, graf, verbálny výraz alebo algebraický vzorec:
- f (x) = x + 1
- Populácia P určitého mesta v určitom časovom intervale t.
- H (x) = (1,3); (2,4); (3,5); (4.6)
Funkcie sa vyznačujú tým, že majú oblasť a rozsah alebo trasa. Doména je množina hodnôt, že premenná X Môžete si vziať, zatiaľ čo rozsah je množina hodnôt, ktoré získavajú závislú funkciu alebo premennú a.
Klasifikácia funkcií
Funkcie môžu byť zoskupené do 5 veľkých kategórií, ako sa odráža v nasledujúcej schéme, v ktorej je každá skupina označená rímskym číslom a farbou. Od zľava doprava sú funkcie klasifikované podľa:
- I) jeho forma.
- Ii) symetria.
- Iii) spôsob vyjadrenia premennej.
- Iv) jej kontinuita a monotónnosť.
- V) Spôsob, akým sú prvky domény spojené s prvkami rozsahu.
 Hlavné klasifikačné kritériá pre funkcie. Zdroj: f. Zapata.
Hlavné klasifikačné kritériá pre funkcie. Zdroj: f. Zapata. Teraz postupujte podľa stručného opisu každého z typov funkcií s ich príslušnými príkladmi.
I) funkcie podľa jeho formy
Jo.1) Algebraické funkcie
Patria medzi najpoužívanejšie funkcie v mnohých oblastiach vedy, a preto sú najznámejšie. Vyznačujú sa tým, že majú ako korešpondenčné pravidlo, algebraický výraz.
Algebraické funkcie sú zase rozdelené do nasledujúcich typov:
- Jo.1.a) polynóm alebo polynóm.
- Jo.1.b) racionálne.
- Jo.1.c) iracionálne.
- Jo.1.d) podľa oddielov.
 Algebraické funkcie a ich typy. Zdroj: f. Zapata.
Algebraické funkcie a ich typy. Zdroj: f. Zapata. Jo.1.a) polynómové alebo polynómové funkcie
 Príklad funkcie polynomického typu. Zdroj: f. Zapata cez geogebra.
Príklad funkcie polynomického typu. Zdroj: f. Zapata cez geogebra. Pozostávajú zo sumy pojmov, ktorých všeobecná forma je:
P (x) = anXn + do N-1XN-1 +..1x + a0
Kde koeficientyn, do N-1..1, do0 Sú to skutočné čísla a n je celé číslo. Doménou polynómových funkcií je sada R reálnych čísel a tiež kontinuálne funkcie v tejto doméne.
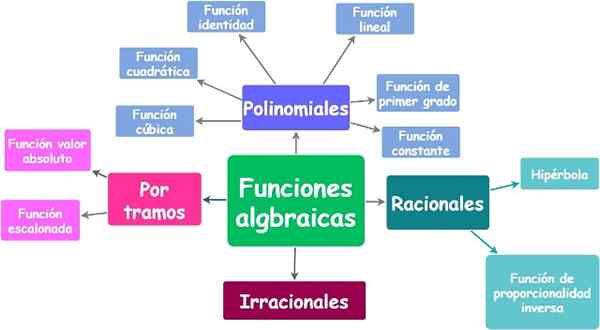
Na hornom obrázku je graf nasledujúcej polynómovej funkcie poradia 4:
f (x) = x4 - 2x2 - x -2
Spomedzi polynómových funkcií sa niektoré konkrétne prípady rozlišujú podľa hodnôt koeficientov. Je potrebné zvážiť opatrne, pretože sú veľmi užitočné vo viacerých situáciách:
i) konštantná funkcia
Existuje konštantná funkcia, keď sú všetky koeficienty zrušené, s výnimkou0:
f (x) = a0 = k
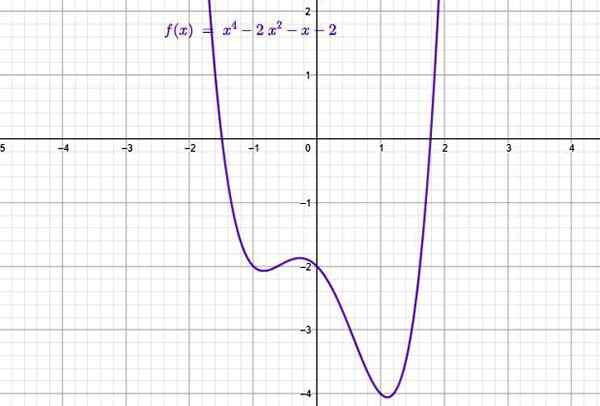
Graf konštantnej funkcie je priamka rovnobežná s horizontálnou osou, napríklad čiary:
- f (x) = 2
- g (x) = π
- H (x) = -3/2
 Dva príklady konštantnej funkcie. Zdroj: f. Zapata.
Dva príklady konštantnej funkcie. Zdroj: f. Zapata. Ii) funkcia prvého stupňa
Prvou -degree funkcia alebo súvisiacou funkciou je, že ktorého graf je priamka. Je to osobitný prípad polynómovej funkcie, kde všetky koeficienty zrušujú1 už0. Je daný:
f (x) = a1x + a0
Hodnota a1 Je to sklon čiary, ktorý dáva mieru jej sklonu a0 Je to rez línie s vertikálnou osou. Obe môžu mať kladné alebo záporné hodnoty.
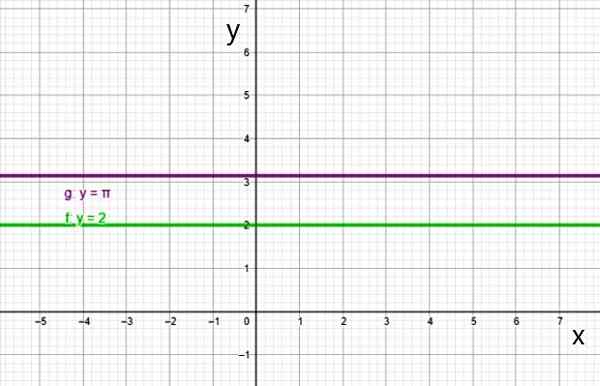
Príklady funkcie prvého stupňa sú nasledujúce:
- G (x) = 2x -1
- H (x) = -6x +5/2
 Funkcia prvého stupňa F (x) = 2x-1. Zdroj: f. Zapata.
Funkcia prvého stupňa F (x) = 2x-1. Zdroj: f. Zapata. Existuje špeciálny prípad, ktorý je lineárnou funkciou.
Môže vám slúžiť: Ústredné opatrenia tendencie pre zoskupené údaje: vzorce, cvičeniaiii) lineárna funkcia
Keď koeficient k0 Je to 0, funkcia vždy prechádza pôvodom a je vyjadrená f (x) = a1X, volanie lemovacia zábava, ako sa máš:
- f (x) = 5x
- G (x) = -7x
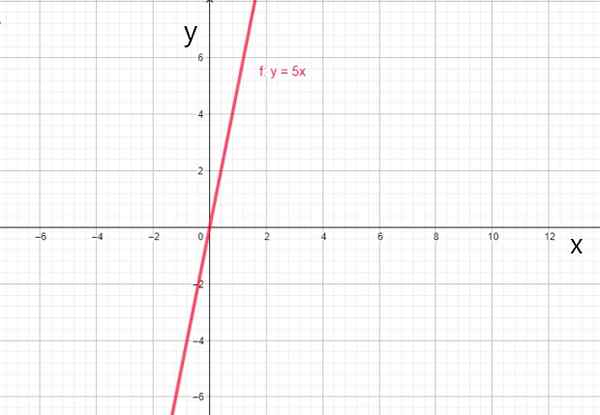 Lineárna funkcia f (x) = 5x. Zdroj: f. Zapata.
Lineárna funkcia f (x) = 5x. Zdroj: f. Zapata. iv) funkcia identity
Je to konkrétny prípad lineárnej funkcie, v ktorej1 = 1:
f (x) = x
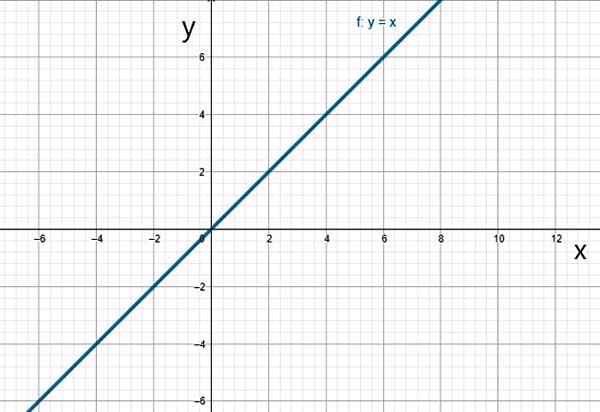 Funkcia identity. Zdroj: f. Zapata.
Funkcia identity. Zdroj: f. Zapata. v) kvadratická funkcia
Má všeobecnú formu:
f (x) = a2X2 +do1x + a0
S2 ≠ 0.
Jeho graf je podobenstvo, ktorého os axiálna alebo symetria je rovnobežná s osou súradnicov. Vždy pretína vertikálnu os v súradnicovom bode x = 0, y = a0. Pokiaľ ide o križovatky s horizontálnou osou, môže mať až maximálne 2.
Príklady kvadratických funkcií sú:
- f (x) = x2 - 3x - 4
- G (x) = 4x2
- H (x) = x2-1
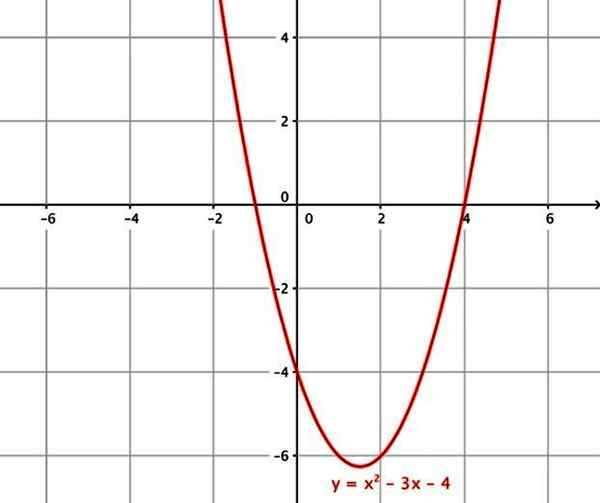 Kvadratická funkcia. Zdroj: Wikimedia Commons.
Kvadratická funkcia. Zdroj: Wikimedia Commons. vi) kubická funkcia
Ako už názov napovedá, kubická funkcia obsahuje výkon 3:
f (x) = a3X3 + do2X2 + do1x + a0
Koeficient a3 Vždy sa líši od 0, ako v týchto prípadoch:
- f (x) = x3
- G (x) = 5x3 - 2
- H (x) = -3x3 + 4x2 + 10x + 1
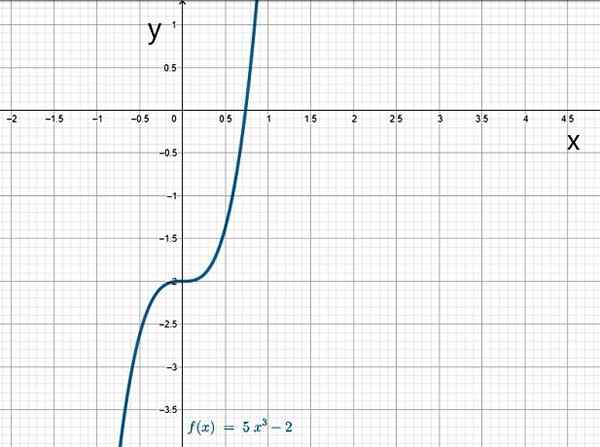 Kubická funkcia. Zdroj: f. Zapata.
Kubická funkcia. Zdroj: f. Zapata. Jo.1.b) racionálne funkcie
Racionálne funkcie majú formu:
=\fracP(x)Q(x))
Z oblasti racionálnych funkcií, všetky hodnoty, ktoré zrušujú menovateľ q (x), to znamená jeho korene, zatiaľ čo hodnoty hodnôt hodnôt a ktoré určujú vodorovné asymptoty.
Asymptot je čiara, ku ktorej sa funkcia blíži, a to vľavo, ako aj vpravo nad alebo pod, ale nikdy neprekročí. Takéto čiary môžu byť vertikálne, vodorovné alebo naklonené.
Príklady racionálnych funkcií sú:
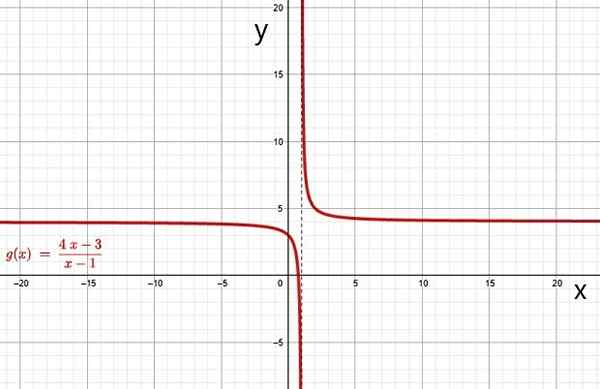 Racionálna funkcia. Zdroj: f. Zapata cez geogebra.
Racionálna funkcia. Zdroj: f. Zapata cez geogebra. i) hyperbola
Graf racionálnej funkcie je hyperbola, keď polynóm v menovateľovi Q (x) má stupeň 1. Graf funkcií F (x) a g (x) vyššie uvedených príkladov sú hyperboly, dá sa ľahko skontrolovať prostredníctvom bezplatného online grafického softvéru, ako je napríklad Geogebra.
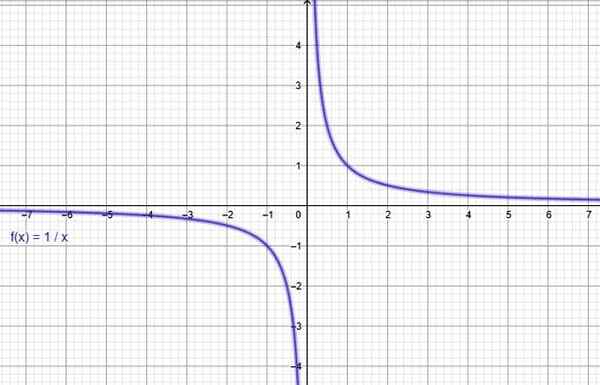 Funkcia y = 1/x. Zdroj: f. Zapata cez geogebra.
Funkcia y = 1/x. Zdroj: f. Zapata cez geogebra. Ii) Funkcia inverznej proporcionality
Je to funkcia formy:
Kde C je skutočné číslo odlišné od 0. Jeho doména je sada skutočných čísel s výnimkou 0.
Jo.1.c) iracionálne funkcie
Sú tí, ktorých nezávislá premenná je pod radikálnym znakom. Jeho všeobecná forma je:
Niektoré z týchto funkcií môžu byť:
Doména týchto funkcií je určená nasledovne:
-Ak sú korene indexu krútiaceho momentu, subradickú sumu f (x) musí byť vždy 0 alebo pozitívne.
-Ak sú korene nepárne, f (x) môže byť pozitívny alebo negatívny. Preto v tomto prípade sú doménou funkcie skutočné čísla.
Napríklad doména:
Je to sada reálnych čísel tak, že x-3 je väčšia alebo rovná 0. V takom prípade musí byť X väčší alebo rovný 3. Preto je doménou tejto funkcie množina hodnôt intervalu [3, ∞+).
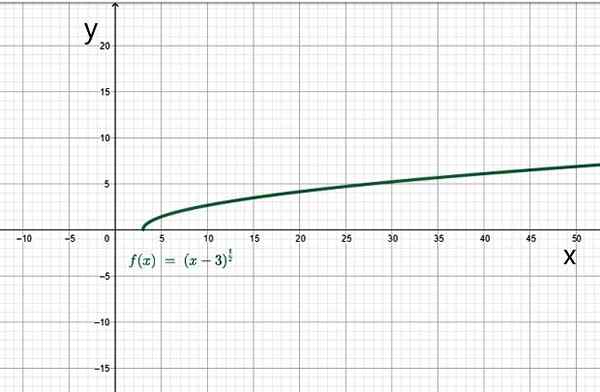 Príklad iracionálnej funkcie. Zdroj: f. Zapata.
Príklad iracionálnej funkcie. Zdroj: f. Zapata. Jo.1.d) funguje na kúsky alebo podľa sekcií
Funkcia v častiach podľa sekcií alebo kusov je taká, ktorá vyžaduje viac ako jeden vzorec pre rôzne hodnoty domény. Tu je niekoľko príkladov vašej žiadosti:
-Sadzby na odosielanie balíkov poštou, v závislosti od hmotnosti alebo objemu, pôvodu a určenia toho istého.
-Ceny pre služby, napríklad telefonovanie a elektrina.
-Predaj lístkov na múzeá alebo zábavné parky v závislosti od veku.
V matematickej forme môže byť napríklad funkcia v častiach:
Doména funkcie v častiach závisí od jej definície. V predchádzajúcom príklade je doména sada vytvorená: (-∞, -1) ∪ [1,+∞).
Ii) Funkcia Escalonada
Graf tejto funkcie podľa sekcií pozostáva z krokov, ako sú kroky rebríka alebo môžu mať rôzne výšky, v závislosti od spôsobu definovanej funkcie.
Môže vám slúžiť: Hipparco z Nicea: biografia a príspevky k vedeZ tohtoJo < x1 < x2 <… . xn A vyberie sa otvorený interval (xJo , Xi+1) Dať mu konštantu hodnoty SJo, S skokmi v bodoch xJo. Hodnota SJo Je to výška príslušného kroku.
Príkladom rozloženej funkcie je celá časť, ktorá berie ľubovoľné číslo a priradí ju s nasledujúcim celkovým číslom, buď prebytkom alebo predvolene. Nasleduje celá časť:
[x] = (väčšie celé číslo ≤ x)
Podľa tejto funkcie celá časť 2.5 je:
[2.5] = (väčšie celé číslo ≤ 2.5) = 2
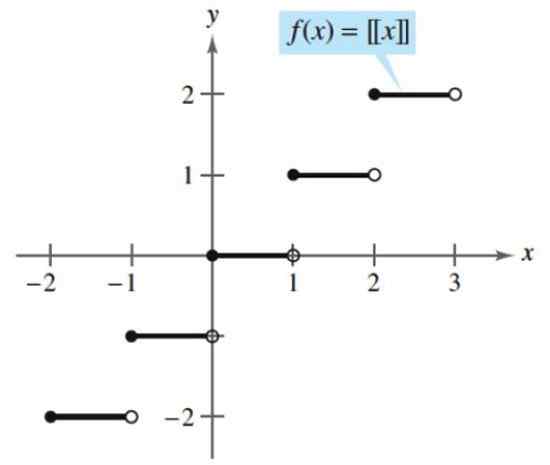 Celá časť. Zdroj: Larson, r. Výpočet analytickou geometriou. McGraw-Hill.
Celá časť. Zdroj: Larson, r. Výpočet analytickou geometriou. McGraw-Hill. Jo.2) transcendentné funkcie
Nealgebraické funkcie sa nazývajú transcendentné. Exponenciálne, logaritmické a trigonometrické funkcie sú transcendentné funkcie.
V nich premenná X Je súčasťou argumentu funkcie alebo ako súčasť exponentu alebo indexu nejakého koreňa, napríklad:
- f (x) = log (x+1)
- H (x) = -0.2 šu-3x
Transcendentné funkcie majú veľa aplikácií, napríklad pri štúdiu vibrácií a vĺn, rozdelenia pravdepodobnosti, modelovanie vĺn, rast rôznych populácií, rádioaktívne rozklady a mnoho ďalších.
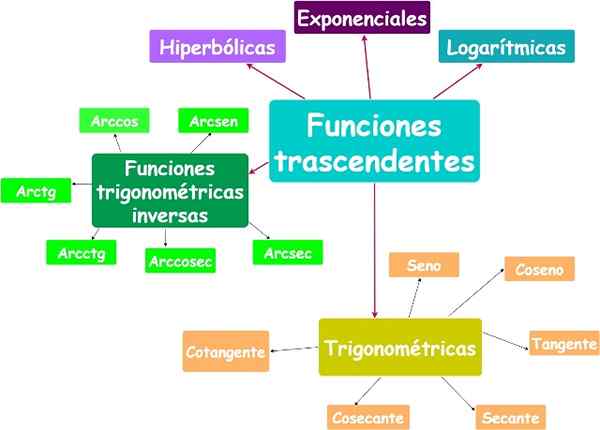 Hlavné transcendentné funkcie. Zdroj: f. Zapata.
Hlavné transcendentné funkcie. Zdroj: f. Zapata. Jo.2.a) Exponenciálna funkcia
Exponenciálna funkcia je definovaná podľa:
f (x) = aX
Kde a je základňa, ktorá je vždy pozitívnym počtom 1 a premenná, skutočné číslo, sa objaví v exponente. Všeobecne je napísaná exponenciálna funkcia:
f (x) = a⋅aBX
Tu sú A a B skutočné koeficienty. Nasledujú funkcie tohto typu:
- f (x) = 5eX
- H (x) = 4. 105x
- g (t) = 8e-2T
Základňa a, kde a Je to počet Euler 2.71828 ..., často sa objavuje v problémoch vedy a inžinierstva, ako aj v štatistikách. Keď má táto základňa, nazýva sa táto základňa Prírodná exponenciálna funkcia.
Doménou exponenciálnej funkcie je sada reálnych čísel, zatiaľ čo rozsah je kladné čísla.
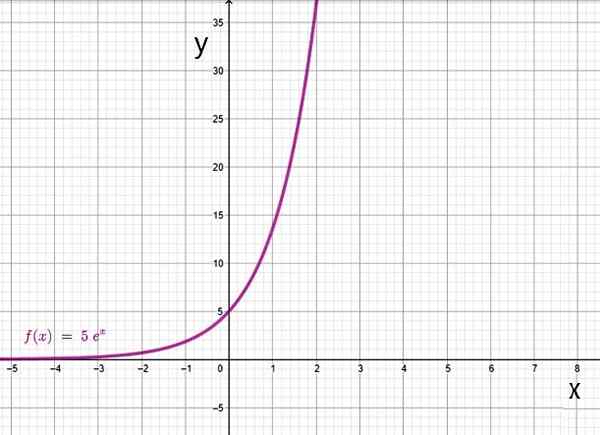 Exponenciálna funkcia založená na. Zdroj: f. Zapata cez geogebra.
Exponenciálna funkcia založená na. Zdroj: f. Zapata cez geogebra. Jo.2.b) funkcia logaritmu
Pokiaľ ide o svoju časť, funkcia logaritmu založená do Je to inverzná funkcia exponenciálnej funkcie založená na do. Áno:
protokoldo x = y
Tak:
x = aa
Najmä ak je základom logaritmu číslo e, funkcia sa volá Funkcia neperiánskeho logaritmu A je označený ako ln. Funkcie tohto typu sú:
- f (x) = ln x
- g (x) = log (x+1)
- H (t) = 1 - log x2
Doména funkcie logaritmu, bez ohľadu na základňu, sú kladné reálne čísla, okrem 0. To znamená, že neexistujú žiadne logaritmy záporných čísel alebo 0.
Logaritmus však môže byť 0 alebo negatívny: logaritmus čísla medzi 0 a 1 je záporný a pre jeho časť dosiahnedo 1 = 0.
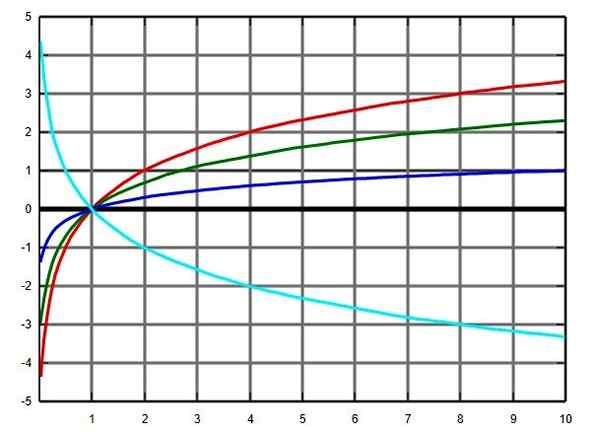 Graf funkcie logaritmu v niekoľkých základniach: Base 2 v červenej, zelenej e, modrej -base a tyrkysová na základni 0.5. Zdroj: Wikimedia Commons.
Graf funkcie logaritmu v niekoľkých základniach: Base 2 v červenej, zelenej e, modrej -base a tyrkysová na základni 0.5. Zdroj: Wikimedia Commons. Jo.2.c) trigonometrické funkcie
Sú to tí, ktorí pochádzajú z trigonometrických dôvodov: sínus, kosínus, dotyčnica, sušenie, harmonické a cotangent uhla x. Sú označené ako:
Sen X, Cos X, Tg X, Sec X, Harm X a Cotg X
Sú to periodické funkcie, čo znamená, že jej forma je opakujúca sa, takže sú veľmi užitočné na opis prírodných javov, ako sú signály, oscilácie, kruhový pohyb a pohyby hojdačky, ktoré sa vyznačujú opakovaním.
Príklady trigonometrických funkcií sú:
- f (x) = sin x
- G (t) = 5⋅cos (Ωt + π)
- H (x) = tg (x/2)
Premenná X je vyjadrená v Radianes.
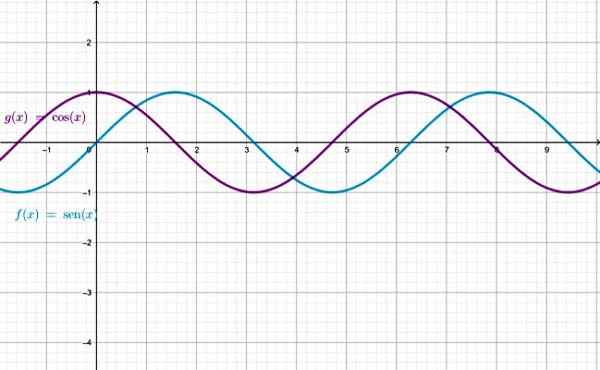 Graf funkcií Sen X a Cos X, všimnite si, že sú identické, s výnimkou toho, že jeden je vysídlený vzhľadom na druhý. Zdroj: f. Zapata cez geogebra.
Graf funkcií Sen X a Cos X, všimnite si, že sú identické, s výnimkou toho, že jeden je vysídlený vzhľadom na druhý. Zdroj: f. Zapata cez geogebra. Majstrovstvá funkcií Sen X a Cos X, je sada skutočných čísel. Pre zostávajúce funkcie existujú hodnoty x, pre ktoré funkcia nie je definovaná:
-Funkcia Tg x neexistuje, keď x = ± π /2, ± 5π /2 ... toto je, všetky nepárne násobky π /2.
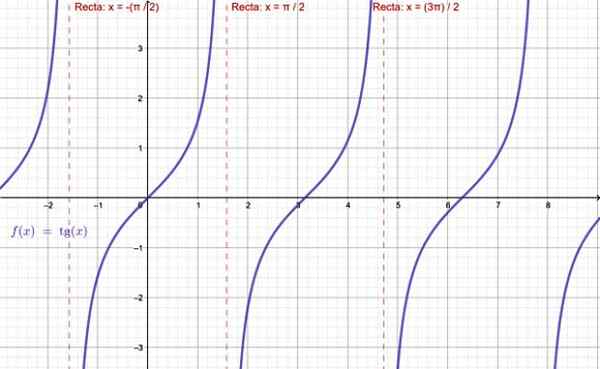 Graf tangentskej funkcie. Zdroj: f. Zapata cez geogebra.
Graf tangentskej funkcie. Zdroj: f. Zapata cez geogebra. -Pokiaľ ide o f (x) = cotg x, táto funkcia nie je definovaná pre celé násobky π: ± π, ± 2π, ± 3π ..
Môže vám slúžiť: Zákon o znakoch-Funkcia y = sec x nie je platná, keď cos x = 0, ktorý vylučuje x = ± π /2, ± 5π /2 ... svojej domény.
-Nakoniec, pre f (x) = poškodenie x, celé násobky π nepatria do ich domény.
Jo.2.d) hyperbolické funkcie
Hyperbolické funkcie sú špeciálnymi kombináciami exponenciálnych aX a e-X A nazývajú sa ako lona, coseno .. .hyperbolický. Rovnako ako v prípade trigonometrických funkcií, ktoré sa tiež nazývajú „kruhové“, existuje 6 hyperbolických funkcií:
-Hyperbolický sínus Senh x:
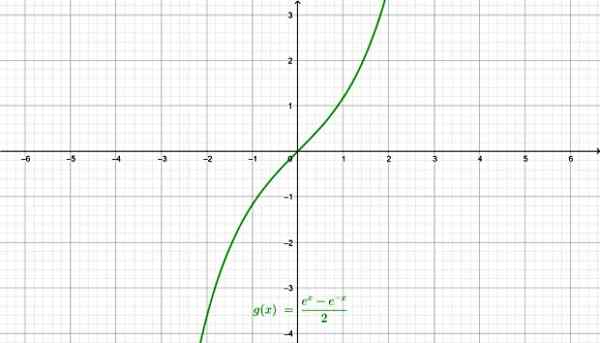 Hyperbolická sínusová funkcia. Zdroj: f. Zapata cez geogebra.
Hyperbolická sínusová funkcia. Zdroj: f. Zapata cez geogebra. -Hyperbolický kosínus Cosh x:



-Hyperbolický cotangent Coth x:
Flexibilný kábel vyrobený z rovnomerného a závesného materiálu medzi dvoma bodmi, má tvar krivky zvanej troska, ktorý je vyjadrený ako hyperbolický kosínus:
Jo.2.e) inverzné trigonometrické funkcie
Zodpovedajú inverzii trigonometrických funkcií. Napríklad, aký by bol uhol (oblúk), ktorého lona má hodnotu 0.5?
Odpoveď je arc sen 0.5, ktoré znie „oblúk sínus 0.5 ”a tento uhol je 30 °, hoci v zásade by to nebol jediný uhol, ktorého lona má hodnotu 0.5, pretože funkcia Sen X je pravidelná. Čo sa stane, je to, že ak sa funkcia Sen X vykonáva v celej doméne, nemala by inverzná, takže funkciu arkroseno nebolo možné definovať. Problém je vyriešený obmedzením všetkého na uhly medzi -π/2 a +π/2.
Toto je možné vyjadriť takto:
Ak je oblúk sen x = 9, znamená to, že sin θ = x
S -π/2 ≤ θ ≤ π/2.
Ďalšou notáciou, ktorá sa používa pre arc sen x je f (x) = hriech-1 X. Graf je uvedený nižšie:
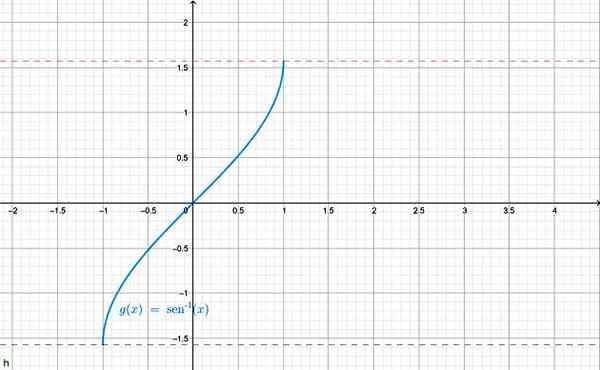 Arcsen X Funkcia grafika. Zdroj: f. Zapata cez geogebra.
Arcsen X Funkcia grafika. Zdroj: f. Zapata cez geogebra. Je tiež možné definovať inverziu pre ďalšie trigonometrické funkcie, napríklad: oblúk cos x = 9 a teda. Pre každú z nich je hodnosť správne obmedzená, je to inverzia zodpovedajúcej trigonometrickej funkcie.
Ii) funkcie podľa jeho symetrie
Ii.1) par
Ak pre všetkých x patriacich do domény f (x) je splnené, že:
f (x) = f (-x)
Hovorí sa, že táto funkcia je rovnomerná, ako tie, ktoré nasledujú:
- f (x) = x2 - 3
- g (x) = cos x
 Príklad funkcie páru. Zdroj: f. Zapata cez geogebra.
Príklad funkcie páru. Zdroj: f. Zapata cez geogebra.
Napríklad, robiť x = 1 in f (x) = x2 - 3 je získané:
f (1) = 12 - 3 = -2.
A ak x = -1, potom:
f (-1) = (-1)2 - 3 = -2.
Oba výsledky sú rovnaké.
Národné funkcie majú symetriu okolo vertikálnej osi, ako je vidieť na predchádzajúcom obrázku.
Ii.2) Čudná funkcia
Na druhej strane áno:
f (-x) = -f (x)
Funkcia je čudná.
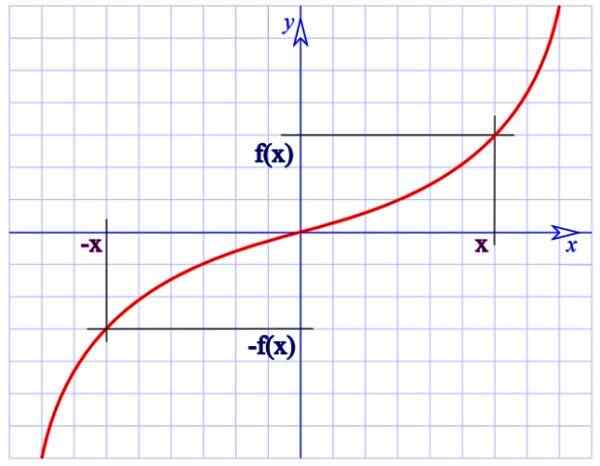 Čudná funkcia. Zdroj: Wikimedia Commons.
Čudná funkcia. Zdroj: Wikimedia Commons. Napríklad funkcia f (x) = 1/x hornej časti je nepárne, pretože:
f (-x) = -1/x
A
-f (x) = -1/x
Ďalšou dôležitou funkciou impar je f (x) = sin x.
Všimnite si, že nepárne funkcie majú okolo pôvodu symetriu rotácie 180 ° (graf sa nezmení, ak je každý bod jeho o 180 ° vzhľadom na pôvod súradníc).
Iii) funkcia podľa expresie premennej
Iii.1) explicitné funkcie
Sú vyjadrené priamo z hľadiska závislej premennej, ako je y = f (x). Napríklad:
- f (x) = x3
Iii.2) Implicitné funkcie
V implicitných funkciách sa zdá, že žiadna z premenných nie je jasná. Sú vyjadrené ako f (x, y) = 0, napríklad:
- X2 + a2 -3xy = 0
- xy = - x2+ X-5
Funkcie opísané v tomto článku sú explicitné funkcie.
Iv) funkcie podľa vašej grafiky
Podľa ich grafu môžu byť funkcie nepretržité alebo diskontinuálne. Kontinuálne funkcie sa dajú vysledovať bez prerušenia zdvihu, na druhej strane, diskontinuálne funkcie predstavujú skoky. Na nasledujúcom obrázku je funkcia diskontinuálna pri x = a:
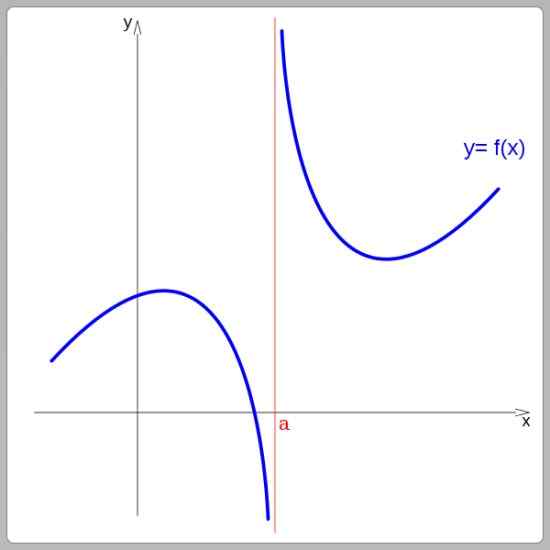 Funkcia diskontinuity pri x = a. Zdroj: Wikimedia Commons.
Funkcia diskontinuity pri x = a. Zdroj: Wikimedia Commons. Príklady kontinuálnych funkcií sú lineárne funkcie, kvadratické funkcie a sínusové a kosínové funkcie. A medzi diskontinuálnymi funkciami patrí rozložená funkcia a dotyčnica.
V) Funkcie podľa vzťahu medzi prvkami domény a rozsahom
Vložka.1) Injektívna funkcia
Funkcia je Injekčný Ak nie sú žiadne dva rôzne prvky v počiatočnej alebo doméne, ktoré majú rovnaký obrázok v množine príchodu.
Predpokladajme, že skutočné funkcie majú, pokiaľ nie sú uvedené inak, napríklad:
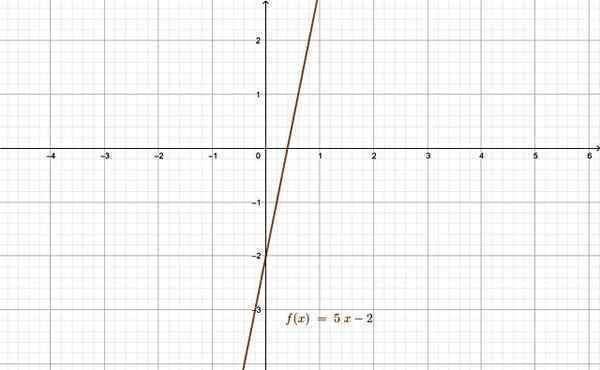
f (x) = 5x -2
Celá hodnota x patriace k doméne F (x), ktorá je nastavená ℛ reálnych čísel, má jedinečný, tiež skutočný obraz. Na druhej strane v tejto inej funkcii:
g (x) = x2
V doméne sú rôzne prvky, ktoré majú rovnaký obrázok, napríklad x1= 2 a x2= -2:
G (2) = g (-2) = 4.
Spôsob, ako identifikovať injekčnú funkciu z jeho grafu, je kreslenie vodorovnej čiary, ak je nakrájaná na krivku vo viac ako jednom bode, funkcia nie je injektívna.
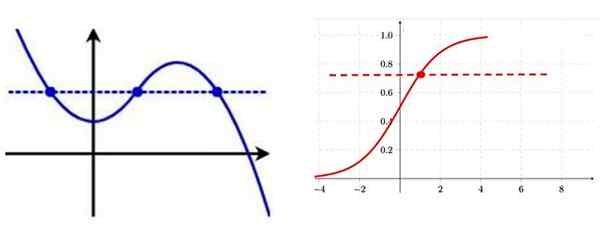 Vľavo injekčná funkcia OSN si všimnite, že existuje niekoľko bodov grafu s rovnakou vertikálnou súradnicou. Vpravo injektívna funkcia, v každom z bodov krivky, má konkrétnu súradnicu „y“. Zdroj: f. Zapata.
Vľavo injekčná funkcia OSN si všimnite, že existuje niekoľko bodov grafu s rovnakou vertikálnou súradnicou. Vpravo injektívna funkcia, v každom z bodov krivky, má konkrétnu súradnicu „y“. Zdroj: f. Zapata. Vložka.2) nadmerná funkcia
V injekčné funkcie, Všetky prvky množiny príchodu sú obrazom niektorých prvkov počiatočnej sady. Príkladom nadmernej funkcie je rovnaký f (x) = 5x -2, ale g (x) = x2 Nie je to tak, pretože hodnoty prijaté g (x) sú iba kladné skutočné a 0.
Doména by sa však mohla nanovo definovať tak, že G (x) bol vpred, ak sa napríklad zmení na všetky pozitívne skutočné plus 0.
Vložka.3) Bijektívna funkcia
Nakoniec sa nazýva funkcia, ktorá je injekčná a nadmerná Bijective. Príklady bijektívnych funkcií sú: súvisiaca funkcia, exponenciálna funkcia a funkcia logaritmu.
 Súvisiaca funkcia je dobrým príkladom bijjektívnej funkcie. Zdroj: f. Zapata cez geogebra.
Súvisiaca funkcia je dobrým príkladom bijjektívnej funkcie. Zdroj: f. Zapata cez geogebra. Odkazy
- E-mata. Typy funkcií. Získané z: emathzone.com.
- Hoffman, J.G. Výber matematických problémov. Edimatizovať. Sphinx.
- Matematika je zábava. Odkaz na funkcie Commons. Získané z: Mathisfun.com.
- Requena, b. Vesmír. Typy funkcií. Získané z: Universoformulas.com.
- Stewart, J. 2006. Predbežné vycvičenie: matematika na výpočet. 5. Vydanie. Učenie sa.
- « Štruktúra Ititrio, vlastnosti, použitie, získanie
- Štruktúra iterbio, vlastnosti, použitie, získanie »


=\frac1x)
=\frac4x-3x-1)
=\frac2-x^2x^2-x-1)
=\fraccx)
)
=\sqrtx-3)
=\sqrt[3]2x^5-7)



=a\cdot&space;cosh\left&space;(\fracxa&space;\right&space;))
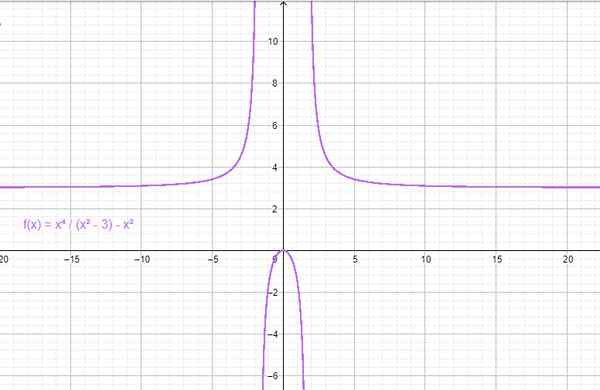
=\fracx^4x^2-3-x^2)