Charakteristika Teseladosu, typy (pravidelné, nepravidelné), príklady

Ten Sklonený Sú to povrchy pokryté jednou alebo viacerými číslami nazývanými Tessely. Sú všade: v uliciach a budovách všetkého druhu. Tessels alebo dlaždice sú ploché kusy, zvyčajne polygóny s zhodnými alebo izometrickými kópiami, ktoré sú umiestnené podľa pravidelného vzoru. Týmto spôsobom neexistujú žiadne priestory bez toho, aby boli zakryté a dlaždice alebo mozaiky sa neprekrývajú. 

V prípade, že sa používa jediný typ mozaiky tvoreného pravidelným mnohouholníkom, potom existuje pravidelný Tesseld, Ale ak sa používajú dva alebo viac typov bežných polygónov, potom je to Polo -regulárny Tesselled.

postava 1. Nepravidelná podlaha dlaždíc, pretože obdĺžniky sú neregistrované polygóny, aj keď sú štvorce. Zdroj: Pixabay.

Nakoniec, keď polygóny, ktoré tvoria Tesseldo, nie sú pravidelné, takže je to nepravidelný.

Najbežnejším typom Tesselda je ten, ktorý tvorí obdĺžnikové a obzvlášť štvorcové mozaiky. Na obrázku 1 máme dobrý príklad.

[TOC]

História Teseladosu

Tessellation sa používa už tisíce rokov na pokrytie podlahových a múrov palácov a chrámov rôznych kultúr a náboženstiev.

Napríklad sumerská civilizácia, ktorá prekvitala okolo 3500 až.C. Na juh od Mezopotámie medzi Eufratmi a Tigris Rivers použili v architektúre šaty.

Obrázok 2. Teselados Sumerios pri dverách Istar. Zdroj: Wikimedia Commons.

Tesels tiež vzbudil záujem matematikov všetkých čias: počnúc Archimedesom v treťom storočí pred Kristom, po ktorom nasledoval Johannes Kepler v roku 1619, Camille Jordan v roku 1880, až do súčasného obdobia s Rogerom Penroseom.

Môže vám slúžiť: frakcia ekvivalentná 3/5 (riešenie a vysvetlenie)

Penrose vytvoril neperiodickú tessellation známu ako Penóza. Atíto Sú to len názvy vedcov, ktorí veľa prispeli k tessellácii.

Pravidelné oká

Pravidelný Teslate sa vyrába s jedným typom pravidelného polygónu. Na druhej strane, aby sa Tesseldo mohol považovať za pravidelný bod lietadla: musí:

-Patria do interiéru mnohouholníka

-Alebo na okraj dvoch susedných polygónov 

-Nakoniec môže patriť do spoločného vrcholu najmenej troch polygónov.

S vyššie uvedenými obmedzeniami sa dá preukázať, že pravidelná tessel môže tvoriť iba rovnostranné trojuholníky, štvorce a šesťuholníky.

Menovanie

Existuje nomenklatúra na označenie Tesels, ktoré spočívajú v zozname v smere ihiel hodín a oddelení bodom, počet strán polygónov, ktoré obklopujú každý uzol (alebo vrchol) Tesselleed, a vždy začínajúc najmenším číslom strany.

Táto nomenklatúra sa vzťahuje na pravidelných a polo -regulárnych časopisov. 

Príklad 1: trojuholníkové Teselado

Obrázok 3 zobrazuje trojuholníkovú pravidelnú dlaždicu. Je potrebné poznamenať, že každý trojuholníkový uzol je spoločným vrcholom šiestich rovnostranných trojuholníkov. 

Spôsob označovania tohto typu Tesselda je 3.3.3.3.3.3, ktoré je tiež označené 3⁶.

Obrázok 3. Trojuholníkové pravidelné Teselado 3.3.3.3.3.3. Zdroj: Wikimedia Commons

Príklad 2: Square Tessel

Obrázok 4 zobrazuje pravidelnú dlaždicu zloženú iba z štvorcov. Je potrebné poznamenať, že každý uzol dlaždíc je obklopený štyrmi zhodnými štvorcami. Zápis, ktorý sa vzťahuje na tento typ štvorcových časov, je: 4.4.4.4 o striedavo 4⁴

Obrázok 4. Štvorcový Tesseld 4.4.4.4. Zdroj: Wikimedia Commons.

Príklad 3: Hexagonal Tesseld

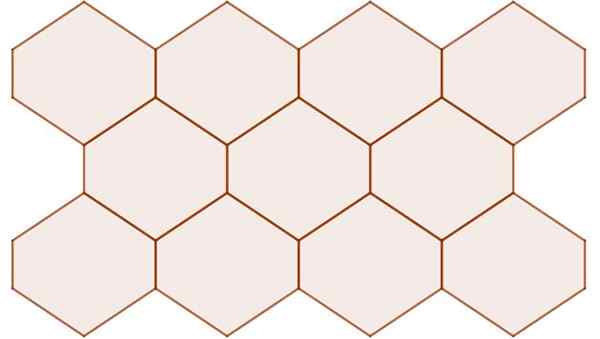
V šesťuholníkovej Tesselle. Nomenklatúra pre pravidelný šesťuholníkový Tessell je 6.6.6 o striedavo 6³.

Môže vám slúžiť: KONICKÉ SEKCIE: Typy, aplikácie, príklady Obrázok 5. Hexagonal Tesseld 6.6.6. Zdroj: Wikimedia Commons.

Polo -regulárny Tesselled

Semi -regulárne alebo tesselované kolo z Archimedes pozostáva z dvoch alebo viacerých druhov pravidelných polygónov. Každý uzol je obklopený typmi polygónov, ktoré tvoria Tessellated v rovnakom poradí a stav okraja je úplne zdieľaná so susedom.

Existuje osem poloregulárnych časopisov:

1. 3.6.3.6 (Tri-hexagonálny Tessell)
2. 3.3.3.3.6 (šesťuholník Teslate Romo)
3. 3.3.3.4.4 (Elongado trojuholníkové Teselado)
4. 3.3.4.3.4 (Romo Square Tesselled)
5. 3.4.6.4 (Rombi-Tri-Hexagonal Tesseld)
6. 4.8.8 (skrátený štvorcový Tessell)
7. 3.12.12 (skrátený šesťuholník Tesseld)
8. 4.6.12 (skrátené tri-hexagonálne Tesseld)

Nižšie sú uvedené niektoré príklady semi -regulárneho Teslate.

Príklad 4: Tixagonal Teselado

Je to ten, ktorý sa skladá z pravidelných rovnostranných trojuholníkov v štruktúre 3.6.3.6, čo znamená, že uzol dlaždíc je obklopený (až kým nedokončí návrat) trojuholníkom, šesťuholníkom, trojuholníkom a šesťuholníkom. Obrázok 6 zobrazuje takúto skúšku.

Obrázok 6. Tri-Hexagonal Tesseld (3.6.3.6) Je to príklad semi -regulárneho Tessellu. Zdroj: Wikimedia Commons.

Príklad 5: Hexagonal Tesseldo Romo

Rovnako ako dlaždica predchádzajúceho príkladu, aj to pozostáva z trojuholníkov a šesťuholníkov, ale jeho distribúcia okolo uzla je 3.3.3.3.6. Obrázok 7 jasne zobrazuje tento typ Tesselled.

Obrázok 7. Hexagonálny Tesseldo Romo pozostáva zo šesťuholníka obklopeného 16 trojuholníkom v konfigurácii 3.3.3.3.6. Zdroj: Wikimedia Commons.

Príklad 6: Rombi-Tri-hexagonálna Tessel

Je to dlaždica, ktorá sa skladá z trojuholníkov, štvorcov a šesťuholníkov, v konfigurácii 3.4.6.4, ktorý je znázornený na obrázku 8.

Obrázok 8. Semi -regulárny Tessell zložený z trojuholníka, štvorca a šesťuholníka v konfigurácii 3.4.6.4. Zdroj: Wikimedia Commons.

Nepravidelné oká

Nazývajú sa nepravidelné dobytky na tie, ktoré sú tvorené nepravidelnými polygónmi alebo pravidelnými polygónmi, ale ktoré nespĺňajú kritérium, že uzol je vrcholom najmenej troch polygónov.

Môže vám slúžiť: Antidevatívne: vzorce a rovnice, príklady, cvičenia

Príklad 7

Obrázok 9 zobrazuje príklad nepravidelnej dlaždice, v ktorej sú všetky polygóny pravidelné a zhodné. Je to nepravidelné, pretože uzol nie je spoločným vrcholom najmenej troch štvorcov a existujú aj susedné štvorce, ktoré úplne nezdieľajú hranu.

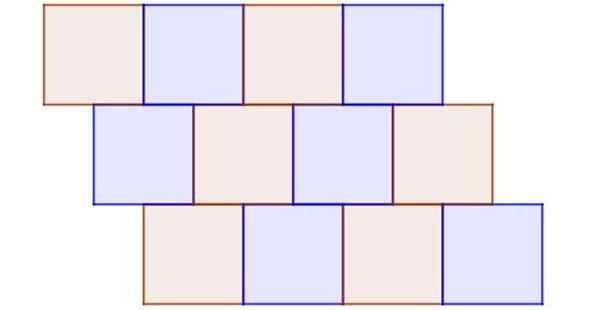Obrázok 9. Aj keď sú všetky dlaždice zhodné štvorce, je to jasný príklad nepravidelného Tesselled. Zdroj: f. Zapata.

Príklad 8

Paralelogram odpadne na rovný povrch, ale pokiaľ nie je štvorcový.

Obrázok 10. Tesseldo tvorený rovnobežníkmi je nepravidelný, pretože jeho mozaiky sú neregistrované polygóny. Zdroj: f. Zapata.

Príklad 9

Neregistrované šesťuholníky s centrálnou symetriou nastavujú rovný povrch, ako je to znázornené na nasledujúcom obrázku:

Obrázok 11. Šesťuholníky s centrálnou symetriou, aj keď nie sú pravidelné, nastavili lietadlo. Zdroj: f. Zapata.

Príklad 10: El Cairo Teselado

Je to veľmi zaujímavá tessellácia, zložená z pentagónov s bokmi rovnakej dĺžky, ale s nerovnakými uhlami, z ktorých dva sú rovné a ďalšie tri majú 120 °.

Jeho meno prichádza, že tento Tesseld je v chodníku niektorých ulíc Káhiry v Egypte. Obrázok 12 zobrazuje Tesseldo z Káhiry.

Obrázok 12. Káhira Tesseldo. Zdroj: Wikimedia Commons.

Príklad 11: Teselado al-Andalus

Tesseldo v niektorých častiach Andalúzie a severnej Afriky sa vyznačuje geometriou a epigrafom, okrem okrasných prvkov, ako je vegetácia. 

Palacios's Tesselled, ako je napríklad Alhambra zložená z dlaždíc tvorených keramickými kúskami mnohých farieb, s viacerými (nehovoriacimi sa nekonečnými) formami, ktoré vyvolali geometrické pozemky.

Obrázok 13. Teselado Palacio de la Alhambra. Tartaglia / verejná doména

Príklad 12: Teselado vo videí

Známy tiež ako Tesellation, je to jeden z najprvosve vo videohrách. Toto je vytvorenie textúr na simuláciu Tesseldu rôznych scenárov, ktoré sa objavujú v simulátore.

Toto je jasná reflexia, že tieto obaly sa naďalej vyvíjajú prenosom hraníc reality.

Odkazy

1. Užite si matematiku. Výplach. Získané z: Vychutnajte si.com
2. Rubiños. Tesels vyriešené príklady. Obnovené z: matematiky.Blog.com
3. Weisstein, Eric W. „Deiregula Tessellation“. Weisstein, Eric W, Ed. Matematický svet. Výskum Wolfram.
4. Wikipedia. Sklonený. Obnovené z: je.Wikipedia.com
5. Wikipedia. Pravidelný Tesseld. Obnovené z: je.Wikipedia.com