Aplikácie, experimenty a cvičenia v Newtone v Newtone

Ten Newtonov tretí zákon, tiež nazývaný Zákon o konaní a reakcii Potvrdzuje, že keď objekt vyvíja silu pred iným, ten tiež uplatňuje na prvú silu rovnakej veľkosti a smeru a opačného zmyslu.

Isaac Newton vydal svoje tri zákony v roku 1686 vo svojej knihe Filozofia naturalis princia matematica alebo matematické princípy prírodnej filozofie.

Vesmírna raketa dostáva potrebný pohon vďaka plynným vylúčeným. Zdroj: Pixabay.

[TOC]

Vysvetlenie a vzorce

Matematická formulácia tretieho zákona Newtona je veľmi jednoduchá:

F₁₂ = -F_{dvadsaťjeden}

Jedna zo síl sa volá akcia A druhý je reakcia. Je však potrebné zdôrazniť dôležitosť tohto detailu: obaja konajú na rôzne objekty. Robia to tiež súčasne, hoci táto terminológia nesprávne naznačuje, že k akcii dochádza predtým a reakcia po.

Pretože sily sú vektormi, sú označené tučným písmom. Táto rovnica naznačuje, že existujú dva objekty: Object 1 a Object 2. Sila F₁₂ Je to ten, ktorý cvičí objekt 1 na objekte 2. Sila F_{dvadsaťjeden} sa uplatňuje podľa objektu 2 na objekte 1. A znamenie (-) poukazuje na to, že sú proti.

Pri starostlivom pozorovaní Newtonovho tretieho zákona je dôležitý rozdiel s prvými dvoma: Zatiaľ čo vyvolávajú jeden objekt, tretí zákon sa týka dvoch rôznych objektov.

A ak si dôkladne myslíte, interakcie vyžadujú páry objektov.

Preto nie sú sily pôsobenia a reakcie zrušené alebo vyvážené, hoci majú rovnakú veľkosť a smer, ale inak: sú aplikované v rôznych telách.

Žiadosti

Interakcia lopty - Zem

Tu je veľmi denná aplikácia interakcie súvisiace s tretím zákonom Newtona: lopta, ktorá spadá vertikálne a Zem. Lopta padá na zem, pretože Zem vyvíja silu príťažlivosti, ktorá je známa ako gravitácia. Táto sila spôsobuje, že lopta klesne s neustálym zrýchlením 9.8 m/s².

Avšak takmer nikto nemyslí na skutočnosť, že lopta tiež vyvíja silu príťažlivosti na Zemi. Zem samozrejme zostáva nezmeniteľná, pretože jej hmota je oveľa väčšia ako hmota lopty, a preto prežíva opovrhnuteľné zrýchlenie.

Ďalším pozoruhodným problémom tretieho zákona Newtona je, že kontakt medzi dvoma objektmi, ktoré interagujú, nie je potrebný. Je to zrejmé s príkladom, ktorý bol práve citovaný: lopta stále neprichádza do kontaktu so Zemou, napriek tomu napriek tomu vykonáva svoju príťažlivosť. A tiež lopta na zemi.

Sila ako gravitácia, ktorá pôsobí zameniteľne, ak existuje kontakt medzi objektmi, akoby neexistovala názov „sily na vzdialenosť“. Namiesto toho sily, ako je trenie a normálne, vyžadujú, aby boli objekty, ktoré interagujú, v kontakte, takže sa nazývajú „kontaktné sily“.

Vzorce extrahované z príkladu

Vráťte sa k niekoľkým loptovým predmetom - Zem, získanie sadov P pre loptu a T pre Zem a získanie Newtonovho druhého zákona na každého účastníka tohto systému sa získajú:

Môže vám slúžiť: diskrétna premenná: Charakteristiky a príklady

F_výsledný = m.do

Tretí zákon uvádza, že:

m_Pdo_P = - m_Tóndo_Tón

do_P = 9.8 m/s² nasmerované vertikálne nadol. Pretože tento pohyb sa uskutočňuje pozdĺž vertikálneho smeru, je možné vydať vektorový zápis (tučný čas); A výber smeru nahor tak pozitívny a dole ako negatívny, máte:

do_P = 9,8 m/s²

m_Tón ≈ 6 x 10 ²⁴ Kg

Bez ohľadu na hmotnosť gule je zrýchlenie Zeme nula. Preto sa pozoruje, že lopta padá na zem a nie naopak.

Prevádzka rakety

Rakety sú dobrým príkladom uplatňovania tretieho zákona Newtona. Raketa zobrazená na obrázku na začiatku stúpa vďaka pohonu horúceho plynu pri vysokej rýchlosti.

Mnohí veria, že sa to stáva, pretože tieto plyny nejako „podporujú“ atmosféru alebo na zemi, aby sa podopreli a tlačili raketu. Takto to nefunguje.

Keď raketa vyvíja silu na plyny a vylučuje ich späť, plyny vyvíjajú silu na raketu, ktorá má rovnaký modul, ale opačný smer. Táto sila je tá, ktorá poskytuje rakete jej zrýchlenie hore.

Ak ich nemáte ručne, existujú aj iné spôsoby, ako overiť, či Newtonov tretí zákon pracuje na poskytovaní pohonu. Môžu sa vybudovať vodné rakety, v ktorých je potrebný ťah ponúkaný vodou na tlakový plyn.

Je potrebné poznamenať, že začiatok vodnej rakety si vyžaduje čas a vyžaduje si veľa preventívnych opatrení.

Používanie korčule

Cenovo dostupnejší a okamžitejší spôsob, ako overiť účinok tretieho zákona Newtona, je umiestnenie niekoľkých korčúľ a propagácia múru.

Väčšinu času je spojená schopnosť vyvíjať silu s objektmi, ktoré sú v pohybe, ale pravdou je, že imobilné objekty môžu tiež uplatňovať silu. Korčuliar je odvedený späť vďaka sile, ktorú na ňu nehybne uplatňuje.

Kontaktné povrchy navzájom vyvíjajú kontaktné sily (normálne). Ak je kniha podporovaná na vodorovnej tabuľke, uplatňuje na ňu normálnu vertikálnu silu. Kniha uplatňuje na tabuľku vertikálnu silu rovnakej číselnej hodnoty a opačného zmyslu.

Detský experiment: korčuliari

Deti a dospelí môžu zažiť Newtonov tretí zákon a overiť, že akcie a reakčné sily nie sú zrušené a sú schopné poskytnúť pohyby.

Každý z korčuliarov na ľade alebo na veľmi hladkom povrchu je možné poháňať.

Zvážte dvoch korčuliarov s celkom odlišným cestom. Sú uprostred ľadového štadióna s opovrhnuteľným trením a spočiatku sú v pokoji. V danom okamihu sa navzájom tlačia a aplikujú konštantnú pevnosť s dlaňami rúk. Ako sa budú pohybovať?

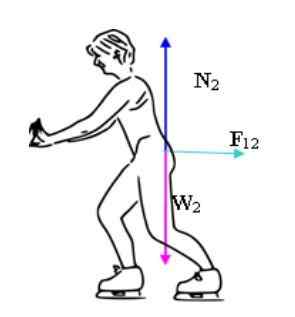
Môže vám slúžiť: vyváženie vektora: výpočet, príklady, cvičeniaDvaja korčuliari sú poháňané uprostred klziska. Zdroj: Benjamin Crowell (používateľ Wikipedia Bcrowell) [CC BY-SA 3.0 (http: // creativeCommons.Org/licencie/By-SA/3.0/]]

Je dôležité zdôrazniť, že keďže je to povrch bez trenia, jediné nevyvážené sily sú sily, ktoré korčuliari navzájom používajú. Zatiaľ čo hmotnosť a normálna konajú na obidvoch z nich, tieto sily sú vyvážené, z toho, čo by korčuliari zrýchlili vo vertikálnom smere.

V tomto príklade sa uplatňovali vzorce

Newtonov tretí zákon uvádza, že:

F₁₂ = -F_{dvadsaťjeden}

To znamená, že sila vyvíjaná korčuliarom 1 na 2 je rovnaká v rozsahu, na ktorú 2 2 vyvíjajú na 1, s rovnakým smerom a opačným smerom. Všimnite si, že tieto sily sa uplatňujú na rôzne objekty, rovnako ako sily boli na lopte a Zemi v predchádzajúcom koncepčnom príklade.

m₁ do₁ = -m₂ do₂

Pretože sily sú opačné, zrýchlenia, ktoré spôsobia. Pozrime sa na zrýchlenie získané prvým korčuliarom:

Ak je hmotnosť prvého korčuliarov vyššia ako hmotnosť druhej, jeho zrýchlenie bude nižšie. Dá sa to očakávať, pretože má väčšiu zotrvačnosť. Najľahší korčuliar získava väčšie zrýchlenie. Ak sú masy rovnaké, zrýchlenia budú tiež.

Takže pohyb, ktorý sa deje nižšie, je oddelenie oboch korčuliarov v opačných zmysloch. V zásade boli korčuliari v pokoji uprostred trate. Každý vyvíja silu na druhej, ktorá poskytuje zrýchlenie, zatiaľ čo ruky sú v kontakte a ťah trvá.

Potom sa korčuliari odvádzajú od seba jednotkovým priamym pohybom tým, že nekonajú nevyvážené sily. Rýchlosť každého korčuliara sa bude líšiť, ak sú aj ich masy.

Cvičenie

Na riešenie problémov, v ktorých sa musia uplatňovať Newtonove zákony, je potrebné starostlivo nakresliť sily, ktoré konajú na objekte. Tento výkres sa nazýva „diagram voľného tela“ alebo „izolovaný diagram tela“. V tomto diagrame by sily, ktoré telo vyvíja na iné objekty, nemali byť zobrazené.

Ak je do problému zapojený viac ako jeden objekt, je to potrebné.

1- korčuliari predchádzajúcej sekcie majú príslušné masy m₁ = 50 kg a m₂ = 80 kg. Tlačili sa s konštantnou silou 200 N. Ťah má trvanie 0.40 sekúnd. Nájsť:

a) Zrýchlenie získané každým korčuliarom vďaka ťahu.

b) rýchlosť každého z nich, keď sa oddeľujú

Riešenie

a) Berte ako horizontálnu pozitívnu adresu, ktorá prechádza zľava doprava. Uplatňovanie Newtonovho druhého zákona s hodnotami poskytnutými vyhlásením je:

F_{dvadsaťjeden} = m₁do₁

Odkiaľ:

Pre druhého korčuliara:

b) Na výpočet rýchlosti, ktorú prenášajú, sa používajú kinematické rovnice rovnomerne zrýchleného priamočiarého pohybu:

Môže vám slúžiť: vzájomná indukčnosť: vzorec/koeficient, aplikácie, cvičenia

Počiatočná rýchlosť je 0, pretože boli v pokoji uprostred trate:

vložka_F =

vložka_F1 = a₁t = -4 m/s² . 0.40 s = -1.6 m/s

vložka_F2 = a₂T = +2.5 m/s² . 0.40 s = +1 m/s

Výsledky

Ako sa očakávalo, osoba 1 je ľahšia, získava väčšie zrýchlenie, a teda rýchlejšiu rýchlosť. Teraz sledujte nasledujúce informácie o produkte cesta kvôli rýchlosti každého korčuliarov:

m₁ vložka₁ = 50 kg . (-1.6 m/s) = - 80 kg.pani

m₂ vložka₂ = 80 kg . 1 m/s = +80 kg.pani

Súčet oboch výrobkov je 0. Produkt hmotnosti podľa rýchlosti sa nazýva množstvo pohybu P. Je to vektor s rovnakým smerom a zmyslom pre rýchlosť. Keď boli korčuliari v pokoji a ich ruky v kontakte, bolo možné predpokladať, že vytvorili rovnaký objekt, ktorého množstvo pohybu bolo:

P_ani = (m₁ +m₂) v_ani = 0

Po dokončení ťahu zostáva množstvo pohybu systému korčuľovania 0. Preto sa zachováva množstvo pohybu.

Príklady Newtonovho tretieho zákona v každodennom živote

Prechádzať sa

Chôdza je jedným z najod dennej akcie, ktoré je možné vykonať. Ak sa starostlivo pozoruje, chôdza vyžaduje tlačenie chodidla na zem, aby vrátila rovnakú a opačnú silu na úpätí chodca.

Keď sme neustále uplatňovali Newtonov tretí zákon. Zdroj: Pixabay.

Je to práve tá sila, ktorá umožňuje ľuďom chodiť. Na lete vtáky vyvíjajú pevnosť na vzduchu a vzduch tlačí krídla tak, aby vták poháňal dopredu.

Pohyb automobilu

V aute kolesá uplatňujú pevnosť na chodníku. Vďaka reakcii na chodník vyvíja sily pneumatík, ktoré poháňajú auto dopredu.

Šport

V športovej praxi sú akčné a reakčné sily početné a majú veľmi aktívnu účasť.

Pozrime sa napríklad na atléta s nohou podporovanou štartovacím blokom. Blok poskytuje normálnu silu ako reakciu na ťah, ktorý na ňu pôsobí športovec. Výsledok tohto normálu a hmotnosti chodby vedie k horizontálnej sile, ktorá umožňuje športovcovi ísť vpred.

Športovec používa štartovací blok na pridanie impulzu vpred na výstup. Zdroj: Pixabay.

Hadici

Ďalším príkladom, v ktorom je prítomný Newtonov tretí zákon. Koniec týchto veľkých hadíc má rukoväť na dýze, ktorú musí hasič držať, keď vyjde vodný prúd, aby sa predišlo neúspechu, ku ktorému dôjde, keď voda vyjde plnou rýchlosťou.

Z toho istého dôvodu je to vhodné.

Odkazy

1. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. Šieste vydanie. Sála. 80 - 82.
2. Rex, a. 2011. Základy fyziky. Pearson. 73 - 75.
3. Tipler, P. 2010. Fyzický. Zväzok 1. 5. vydanie. Redaktor sa vrátil. 94 - 95.
4. Stern, D. 2002. Astronómy k astronaves. Prevzaté z: PWG.GSFC.hrniec.Vláda.