Miletus Taká veta

Vysvetlíme prvú a druhú vetu takejto, s vyriešenými príkladmi a cvičeniami

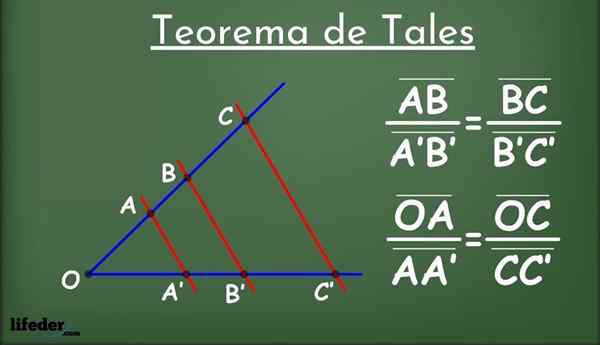postava 1.- Talesova veta

Čo je také?

On taká veta Z Miletus sa v skutočnosti odvoláva na niekoľko geometrických vety pripisovaných múdrym starovekým Gréckom Thalesom z Miletusu, ktorý žil od 624 do 546 AC v Miletus v súčasnom Turecku.

Okrem matematika a geometru bol taký filozof uznaný za svoju veľkú ostrosť. Hovorí sa, že sa mu podarilo zmerať výšku veľkej pyramídy pomocou jednej z jeho vety.

On Prvá veta takýchto Vzťahuje sa na segmenty, ktoré skupina paralelných línií určuje v dvoch riadkoch v rovine. Tieto segmenty udržiavajú pomer proporcionality, ako bude vidieť čoskoro, čo je rozšírené na strany dvoch trojuholníkov za predpokladu, že sú splnené určité podmienky.

Táto veta je v praxi mimoriadne užitočná, pretože umožňuje určiť výšku veľmi vysokých alebo ťažko prístupných štruktúr, bez toho, aby ich musela priamo zmerať. To bolo presne to, čo urobil príbehy, keď meral výšku veľkej pyramídy.

Po jeho časti Druhá veta tohto Spojovacie body, ktoré patria k obvodu s registrovaným trojuholníkom obdĺžnika, ktorého hypotenus sa zhoduje s jej priemerom.

Prvá veta takýchto

Byť dvoma čiarami v lietadle, nazývané L₁ a l₂ (v modrej na obrázku 1) a skupina riadkov rovnobežných navzájom (v červenej), ktorá pretína l₁ a l₂.

Paralelné čiary rozdeľujú čiary na segmenty l₁ a l₂: Ab, a'b ', bc, b'c' a tak ďalej. Spomedzi segmentov, ktorým čelia, je stanovený nasledujúci vzťah proporcionality:

Napríklad na tomto obrázku sa miera segmentu „x“ vypočíta podľa vety takéhoto, pretože čiary sú pretínané niekoľkými paralelami, ktoré určujú segmenty so známou dĺžkou:

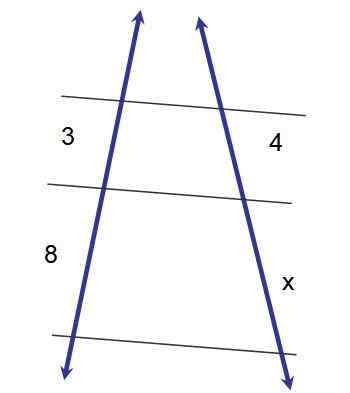Môže vám slúžiť: vzájomne sa vylučujú udalosti: Vlastnosti a príkladyObrázok 2.- Aplikácia prvej takejto vety na určenie miery segmentu x. Zdroj: f. Zapata.

3x = 32

x = 32/3 ≈ 10.7

Taká veta pre podobné trojuholníky

Veta sa dá rozšíriť na trojuholníky nasledovne: Predpokladajme, že existuje trojuholník ABC, na ktorom je paralelný segment nakreslený na jednu zo svojich strán. Týmto spôsobom sa získajú dva podobné trojuholníky: ABC a DEC, ktorých vnútorné uhly sú zhodné, to znamená, že majú rovnakú mieru.

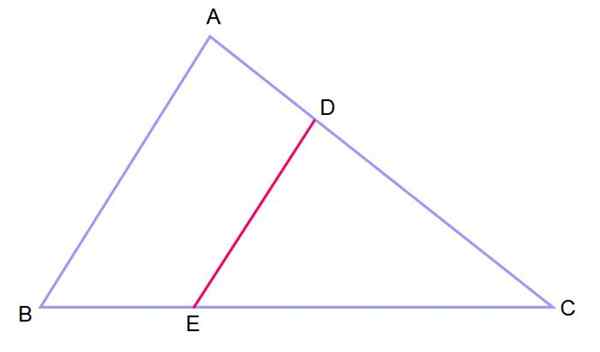Obrázok 3.- Dva trojuholníky v polohe takejto, s dvoma rovnobežnými stranami a spoločným uhlom sú podobné. Zdroj: f. Zapata.

Ak máte dva trojuholníky usporiadané týmto spôsobom, hovorí sa, že sú v takej pozícii.

Pomer proporcionality medzi segmentmi sa zvyšuje rovnakým spôsobom ako pre paralelné čiary:

Čo je rovnocenné s týmto druhým, medzi zodpovedajúcimi stranami každého trojuholníka, tiež nazývaných homológne strany:

Každý z týchto kvocientov sa volá dôvod. V podobných trojuholníkoch sa dôvod podobnosti rovná kvocientu medzi obvodmi a štvorcom pomeru podobnosti.

Ďalej, príklad, v ktorom je možné takúto vetu aplikovať na podobné trojuholníky a zistiť, koľko neznáma strana X stojí za to.

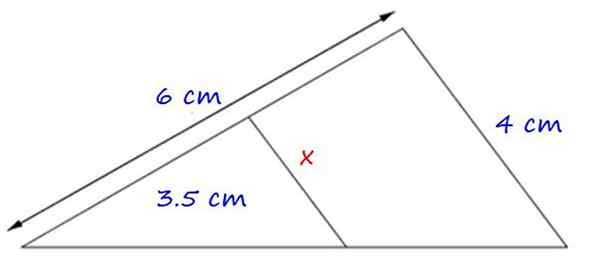Obrázok 4.- Príklad aplikácie prvej takejto vety. Zdroj: f. Zapata.

Vytvorené trojuholníky sú podobné, pretože majú spoločný uhol a strany x a 4 cm sú rovnobežné.

Preto proporcionalita medzi zodpovedajúcimi stranami je:

A hodnota X sa ľahko vymaže:

x = (4 × 3.5) ÷ 6 cm = 2.3 cm

Druhá veta tohto

Táto veta sa vzťahuje na trojuholník, ktorého vrcholy sú body, ktoré patria k obvodu, čo znamená, že je v nej zaregistrovaná.

V tomto prípade veta uvádza, že vždy, keď hypotenusa zodpovedá priemeru obvodu, takto sledovaný trojuholník je obdĺžnik, to znamená jeden z jeho vnútorných uhlov 90 °, ako je vidieť na obrázku 5 vľavo vľavo.

Môže vám slúžiť: Symbolizácia výrazov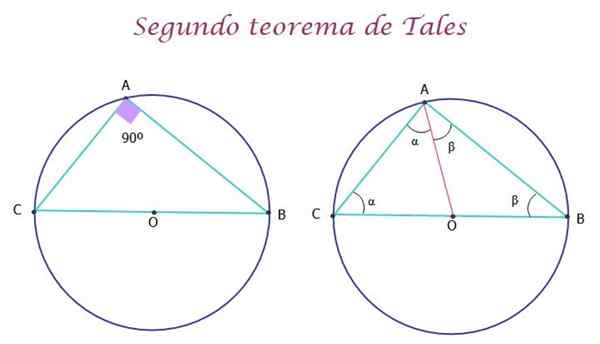Obrázok 5.- Druhá veta takýchto štátov, že trojuholník zaregistrovaný v obvode je obdĺžnik. Zdroj: f. Zapata.

Demonštrácia druhej vety takýchto

Demonštrácia vety je veľmi jednoduchá. Na obrázku vyššie, segment AO bol nakreslený červenou farbou, za vzniku dvoch trojuholníkov AOC a AOB, ktoré sú izoscely, pretože strany OA, OC a OB sú rádiá obvodov, a preto merajú rovnaké.

Týmto spôsobom majú trojuholníky dva rovnaké uhly, ktoré sú a a p. Teraz, pre pôvodný trojuholník ABC, pokiaľ ide o akýkoľvek trojuholník, je splnené, že súčet opatrení jeho vnútorných uhlov sa teda rovná 180 °:

a + (a + β) + β = 180 °

Teda:

2a + 2p = 180 °

Preto:

2 (a +β) = 180 °

a +β = 90 °

Čo dokazuje, že trojuholník ABC má vnútorný uhol 90 °, a preto je pravým trojuholníkom.

Príklad

Na nasledujúcom obrázku sú trojuholník ABC Isosceles a obdĺžnik (trojuholník izorectangle), ktorý je obvodom obvodu rovnajúci sa 25 cm. Koľko sú segmenty AC a AB?

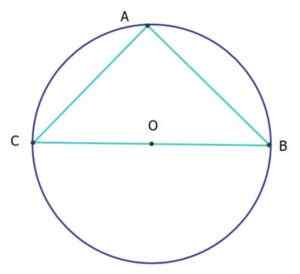
Obvod obvodu je jeho dĺžka l, daná v závislosti od jeho priemeru d podľa vzorca:

L = πD

Preto meria priemer, ktorý je segmentom CB:

D = cb = l/ π = 25 cm/ π = 7.96 cm.

Pretože trojuholník sú izoscely, znamená to, že jeho akútne uhly merajú 45 ° každý. Pretože hypotenus trojuholníka je priemerom obvodu, môže sa použiť trigonometrický pomer 45, napríklad:

Sen 45 ° = AC/CB

AC = CB × Sin 45 ° = 7.96 cm × sin 45 ° = 5.64 cm

Môže vám slúžiť: Moivre veta

Strana AB má rovnaké opatrenie: 5.64 cm, pretože trojuholník je izoscely.

Takéto aplikácie vety

Prvá takáto veta sa dá použiť na poznanie vzdialeností, ktoré nie sú ľahko merateľné. Hovorí sa, že takýto cestoval do Egypta a tam bol veľmi dômyselne výška veľkej pyramídy.

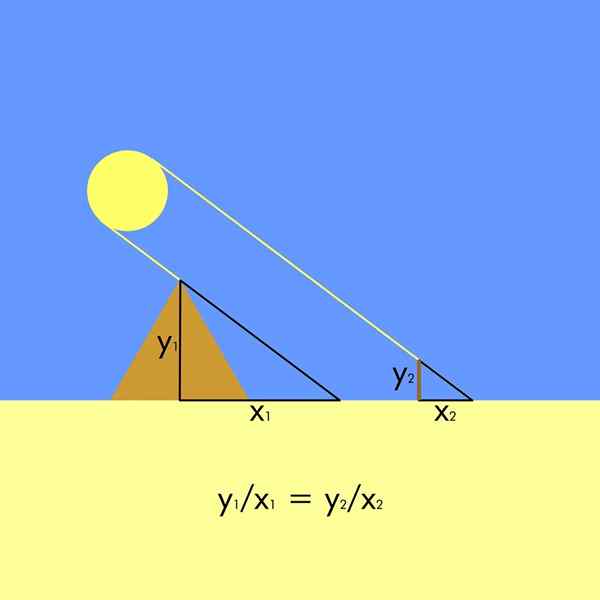
Za to to bolo potrebné. Vytvárajú sa teda dva podobné trojuholníky, pretože slnečné lúče majú paralelný výskyt.

Na obrázku je výška pyramídy a₁ A jeho tieň je x₁, Zatiaľ čo výška vkladu je a₂ (Niektorí kronikári tvrdia, že takto použili svoju vlastnú výšku) a ich tieň je x₂. Keďže sú trojuholníky podobné, vytvára sa nasledujúci vzťahový vzťah:

Veľmi ľahké vyčistiť výšku pyramídy a₁:

a₁ = x₁∙ (a₂ ÷ x₂)

Odkazy

1. Alexander, D. 2013. Geometria. 5. Vydanie. Učenie sa.
2. Requena, b. Taká veta. Získané z: Universoformulas.com.
3. Matematická sála. Tales de Mileto a veľká pyramída. Zdroj: Salonmatematic.com
4. Superprof didaktický materiál. Miletus také. Obnovené z: Superprof.je.
5. Thales a podoba veta. Dva veľmi staré problémy. Získané z: edu.Xunta.Gal.