Lamyho veta
- 1875
- 399
- MUDr. Žigmund Boška

Lamyho veta ustanovuje, že keď je tuhé telo v rovnováhe a pri pôsobení troch zvlnených síl (sily, ktoré sú v rovnakom lietadle), sa ich akčné línie zhodujú v rovnakom bode.
Vetu bola odvodená francúzskym fyzikom a náboženským. Všeobecne sa používa na nájdenie hodnoty uhla, akčnej čiary sily alebo na vytvorenie trojuholníka síl.
Vysvetlenie
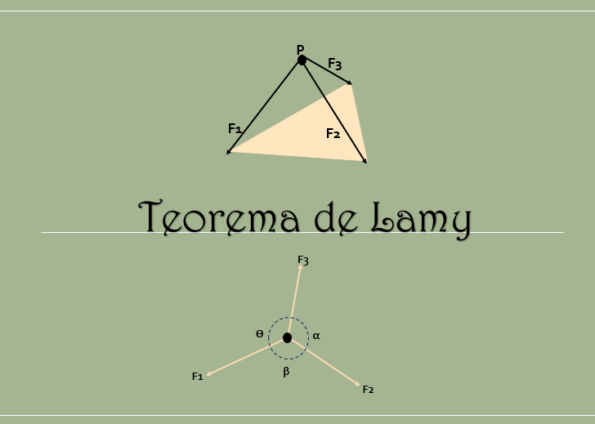
Veta ustanovuje, že na splnenie podmienky rovnováhy musia byť sily koplanáre; to znamená, že súčet síl vyvíjaných v bode je nula.
Okrem toho, ako je vidieť na nasledujúcom obrázku, je splnené, že predĺžením línií pôsobenia týchto troch síl sa zhodujú v rovnakom bode.
Ak teda tri sily, ktoré sú v rovnakej rovine a súbežné, veľkosť každej sily bude úmerná prstencovi opačného uhla, ktoré tvoria ostatné dve sily.
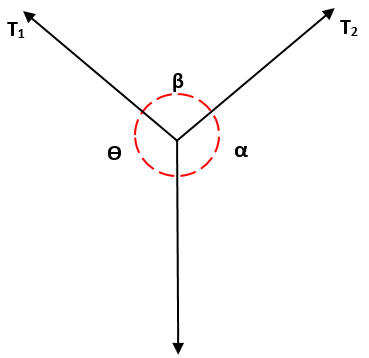
To musí T1, počnúc prsníkom a, sa rovná pomeru T2 / β, čo sa zase rovná pomeru T3 / ɵ, to znamená:
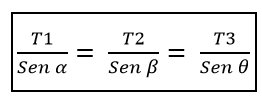
Z toho vyplýva, že moduly týchto troch síl musia byť rovnaké, ak uhly, ktoré tvoria každú dvojicu síl, sa rovnajú 120 °.
Existuje možnosť, že jeden z uhlov je tupý (miera medzi 900 a 1800). V takom prípade sa prsník tohto uhla bude rovnať lone doplnkového uhla (v jeho páre meria 1800).
Môže vám slúžiť: zákony exponentovCvičenie
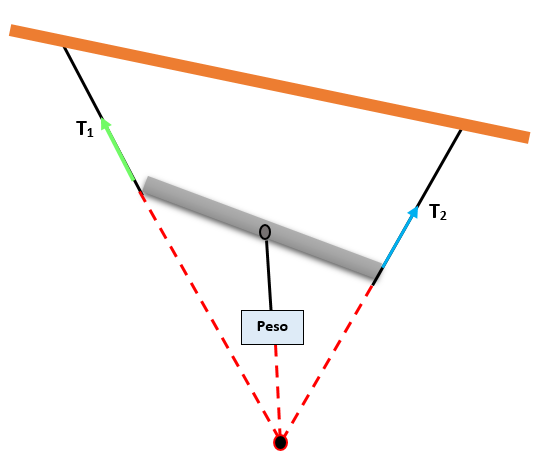
Existuje systém tvorený dvoma blokmi J a K, ktoré visia na niekoľkých reťazcoch, ktoré tvoria uhly vzhľadom na vodorovné, ako je to znázornené na obrázku. Systém je v rovnováhe a blok J váži 240 N. Stanovte hmotnosť bloku K.
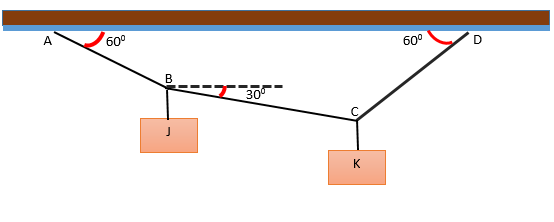
Riešenie
Podľa zásady účinku a reakcie sa napätia vyvíjané v blokoch 1 a 2 bude rovnať hmotnosti týchto.
Teraz je pre každý blok vytvorený voľný diagram tela, a tak určuje uhly, ktoré tvoria systém.
Je známe, že lano, ktoré ide do A až B, má uhol 300 , takže uhol, ktorý ho dopĺňa, sa rovná 600 . Týmto spôsobom dosiahnete 900.
Na druhej strane, kde sa nachádza bod A, je uhol 600 vzhľadom na horizontálne; Uhol medzi zvislým a TDo Bude = 1800 - 600 - 900 = 300.
Získa sa teda, že uhol medzi AB a BC = (300 + 900 + 300) a (600 + 900 + 60) = 1500 a 2100. Pri vstupe sa overuje, že celkový uhol je 3600.
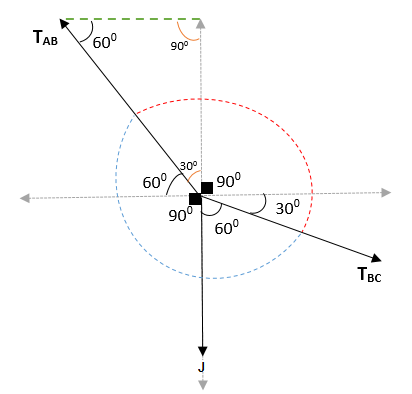
Aplikácia Lamyho vety musíte:
TónBc/ hriech 1500 = PDo/ hriech 1500
TónBc = PDo
TónBc = 240n.
V bode C, kde je blok, uhol medzi vodorovným a BC lane je 300, Takže doplnkový uhol sa rovná 600.
Na druhej strane je uhol 600 v bode CD; Uhol medzi zvislým a TC Bude = 1800 - 900 - 600 = 300.
Môže vám slúžiť: Coplanares body: rovnica, príklad a vyriešené cvičeniaZíska sa teda, že uhol v bloku K je = (300 + 600)
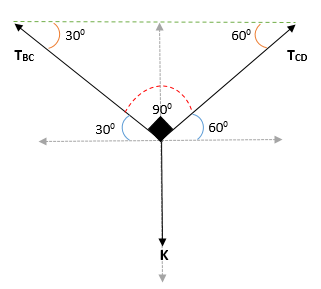
Aplikácia Lamyho vety v bode C:
TónBc/ hriech 1500 = B / sin 900
Q = TBc * Sen 900 / hriech 1500
Q = 240 N * 1/0,5
Q = 480 N.
Odkazy
- Ferdinand p. Pivo, e. R. (2013). Mechanika pre inžinierov, statické. McGraw-Hill Inter-American.
- Francisco Español, J. C. (2015). Vyriešené lineárne problémy s algebrom. Paraninfo Editions, S.Do.
- Graham, J. (2005). Sila a pohyb. Houchton Mifflin Harcourt.
- Harpe, P. d. (2000). Témy v teórii geometrických skupín. University of Chicago Press.
- P. TPLER Y, G. M. (2005). Fyzika pre vedu a techniku. Zväzok I. Barcelona: Vráťte vás.Do.

