Euklidová veta

Čo je Euclidova veta?

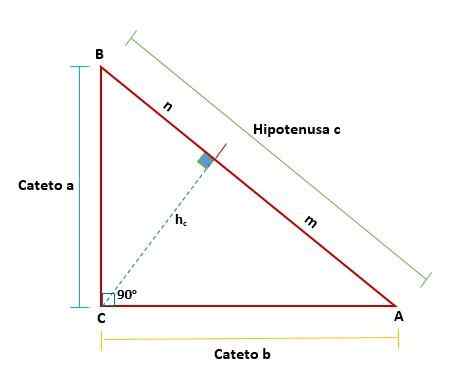
On Euklidová veta Ukazuje vlastnosti pravého trojuholníka nakreslením čiary, ktorá ju delí na dva nové obdĺžniky, ktoré sú navzájom podobné a sú zase podobné pôvodnému trojuholníku; Existuje teda vzťah proporcionality.

Euclides bol jedným z najväčších matematikov a geometrov staroby, ktoré urobili niekoľko demonštrácií dôležitých teorémov. Jeden z hlavných je ten, ktorý nesie jeho meno, ktoré malo širokú aplikáciu.

Bolo to tak preto, že prostredníctvom tejto vety vysvetľujú geometrické vzťahy existujúce v obdĺžnikovom trojuholníku, kde to súvisí s ich projekciami v hypotenuse.

Vzorce a demonštrácia

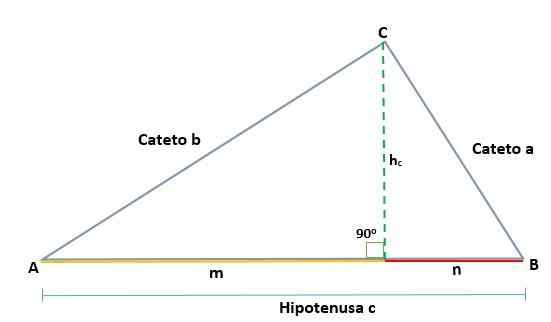
Euklidová veta navrhuje, že v každom pravom trojuholníku, keď je kreslená čiara, ktorá predstavuje vo výške, ktorá zodpovedá vrcholu pravého uhla vzhľadom na hypotenus - dva obdĺžniky sú tvorené z pôvodných trojuholníkov z pôvodného.

Tieto trojuholníky budú navzájom podobné a budú tiež podobné pôvodnému trojuholníku, čo znamená, že ich podobné strany sú navzájom úmerné:

Uhly troch trojuholníkov sú zhodné; To znamená, že keď sa otáča pri 180 stupňoch na svojom vrchole, uhol sa zhoduje na druhej strane. To znamená, že každý bude rovnaký.

Týmto spôsobom môžete tiež overiť podobnosť, ktorá existuje medzi týmito tromi trojuholníkmi, pre rovnosť jej uhlov. Pretože podobnosť trojuholníkov, Euclid stanovuje ich proporcie z dvoch vety:

• Veta výšky.
• Veta Catetos.

Táto veta má širokú aplikáciu. V staroveku sa použil na výpočet výšok alebo vzdialeností, čo predstavuje veľký pokrok pre trigonometriu.

Môže vám slúžiť: výpočet prístupov pomocou diferenciálov

V súčasnosti sa uplatňuje v rôznych oblastiach, ktoré sú založené na matematike, ako je inžinierstvo, fyzika, chémia a astronómia, medzi mnohými ďalšími oblasťami.

Veta výšky

Táto veta ustanovuje, že v akomkoľvek obdĺžnikovom trojuholníku je výška vytiahnutá z pravého uhla vzhľadom na hypotenusu geometrický proporcionálny priemer (štvorcový výška) medzi projekciami Cotetos, ktorý sa určuje na hypotenuse.

To znamená, že štvorec výšky sa bude rovnať násobeniu premietaných nôh, ktoré tvoria hypotenus:

h_c² = m _* n

Demonštrácia

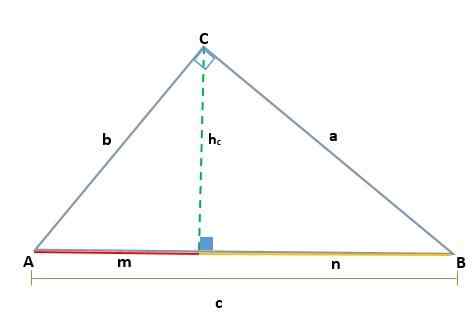
Vzhľadom na trojuholník ABC, ktorý je obdĺžnik vo vrchole C, sa generujú dva podobné obdĺžniky, ADC a BCD; Preto sú ich zodpovedajúce strany úmerné:

Takým spôsobom, že výška h_c Zodpovedá segmentu CD, zodpovedá hypotenuse ab = c, takže musíte:

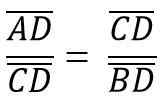
Na druhej strane to zodpovedá:

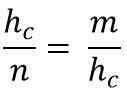
Vyčistenie hypotenus (h_c), Aby ste vynásobili dvoch členov rovnosti, musíte:

h_{C *} h_{C =} m _* n

h_c² = m _* n

Hodnota hypotenusu je teda daná:

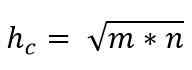
Veta Catetos

Táto veta ustanovuje, že v každom pravom trojuholníku bude miera každého kateto geometrický proporcionálny priemer (štvorec každého kateto) medzi mierou hypotenusu (kompletná) a projekciou každého z nich na ňom:

b² = c _* m

do² = c_* n

Demonštrácia

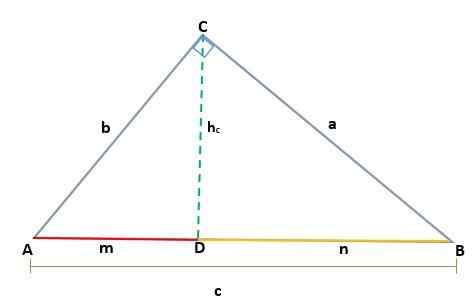
Vzhľadom na trojuholník ABC, ktorý je vo vrchole C obdĺžnik, takže jej hypotenusa je C, keď kreslí výšku (h) projekcie kategórií A a B, ktoré sú segmenty M a N, a ktoré sú zapnuté Hypotenus.

Výška nakreslená na obdĺžnikovom trojuholníku ABC generuje dva podobné obdĺžniky, ADC a BCD, takže zodpovedajúce strany sú proporcionálne, podobne:

Môže vám slúžiť: Hyperbolický paraboloid: Definícia, vlastnosti a príklady

Db = n, čo je projekcia CB kateto na hypotenuse.

Ad = m, čo je projekcia AC kateto na hypotenuse.

Potom je hypotenus C určený súčtom nôh svojich projekcií:

C = m + n

Z dôvodu podobnosti trojuholníkov ADC a BCD musíte:

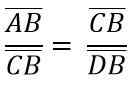
Vyššie uvedené je rovnaké ako:

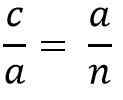
Vyčistenie kateto „A“, aby ste vynásobili dvoch členov rovnosti, musíte:

do _* a = c _* n

do² = c _* n

Hodnota kateta „A“ je teda daná:

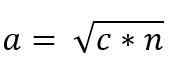
Podobne z dôvodu podobnosti trojuholníkov ACB a ADC musíte:

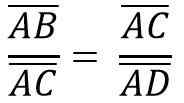
Vyššie uvedené sa rovná:

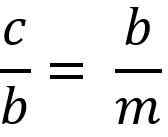
Vyčistenie kateto „B“, aby ste vynásobili dvoch členov rovnosti, musíte:

b _* b = c _* m

b² = c _* m

Hodnota kateta „B“ je teda daná:

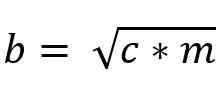
Vzťah medzi euklidovými vetami

Vety s odkazom na výšku a kategórie sú navzájom príbuzné, pretože miera oboch sa vykonáva vzhľadom na hypotenus obdĺžnika trojuholníka.

Prostredníctvom vzťahu euklidových vety možno nájsť aj hodnotu výšky; To je možné vymazaním hodnôt M a n vety kategórie a sú nahradené vo výškovej vete. Týmto spôsobom je splnené, že výška sa rovná násobeniu nôh, vydelená hypotenusom:

b² = c _* m

m = b² ÷ c

do² = c _* n

n = a² ÷ c

Vo výške sa veta M a N vymenia:

h_c² = m _* n

h_c² = (b² ÷ c) _* (² ÷ c)

h_c = (b² _* do²) ÷ c

Vyriešené cvičenia

Príklad 1

Vzhľadom na trojuholník ABC, obdĺžnik v A, určte mieru AC a AD, ak AB = 30 cm a BD = 18 cm

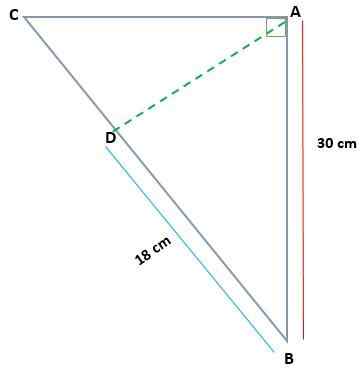
Riešenie

V takom prípade existujú opatrenia jednej z plánovaných nôh (BD) a jednej z tašiek pôvodného trojuholníka (AB). Týmto spôsobom môžete použiť vetu kategórie na nájdenie hodnoty BC Cateto.

Môže vám slúžiť: korešpondenčné pravidlo funkcie

AB² = Bd _* Bc

(30)² = 18 _* Bc

900 = 18 _* Bc

BC = 900 ÷ 18

BC = 50 cm

Hodnota CD kateto sa dá nájsť s vedomím, že BC = 50:

CD = BC - BD

CD = 50 - 18 = 32 cm

Teraz je možné určiť hodnotu AC Cateto a znova uplatniť vetu kategórie:

Ac² = CD _* Bd

Ac² = 32 _* päťdesiat

Ac² = 160

AC = √1600 = 40 cm

Na určenie hodnoty výšky (AD) sa uplatňuje výška vety, pretože hodnoty projektovaných kategórií sú známe CD a BD:

Reklama² = 32 _* 18

Reklama² = 576

AD = √576

AD = 24 cm

Príklad 2

Určite hodnotu výšky (H) trojuholníka MNL, obdĺžnik v n, poznať opatrenia segmentov:

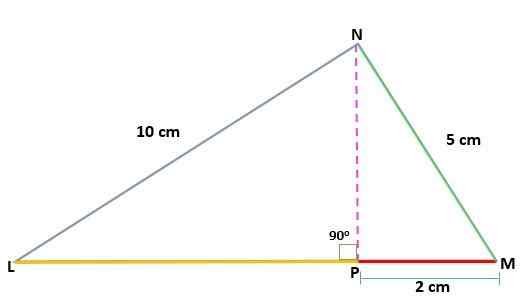
Nl = 10 cm

Mn = 5 cm

PM = 2 cm

Riešenie

Máte mieru jednej z premietaných nôh na hypotenus (PM), ako aj opatrenia pôvodných kategórií trojuholníka. Týmto spôsobom môžete použiť vetu kategórie na nájdenie hodnoty druhého premietaného Cateto (LN):

Nl² = PM _* Lm

(10)² = 5 _* Lm

100 = 5 _* Lm

PL = 100 ÷ 5 = 20

Pretože hodnota kategórií a hypotenus je už známa, prostredníctvom vzťahu výškových vety a kategórií je možné určiť hodnotu výšky:

Nl = 10

Mn = 5

LM = 20

H = (b² _* do²) ÷ c.

H = (10² _* 5²)  ÷ (dvadsať)

H = (100 _* 25) ÷ (dvadsať)

H = 2500 ÷ dvadsať

H = 125 cm.