Chbyshovova veta, ktorá je, aplikácie a príklady

On Chebyshovova veta (alebo nerovnosť Chbyshova) je jedným z najdôležitejších klasických výsledkov teórie pravdepodobnosti. Umožňuje odhad pravdepodobnosti udalosti opísanej z hľadiska náhodnej premennej X, poskytovaním úrovne, ktorá nezávisí od distribúcie náhodnej premennej, ale od rozptylu x.

Veta sa nazýva na počesť ruského matematického.

Táto nerovnosť alebo tie, ktoré sa kvôli ich charakteristikám nazývajú nerovnosť Chbyshova, sa používa hlavne na približné pravdepodobnosti pomocou výpočtu úrovní.

Čo je to Chebyshovova veta?

V štúdii teórie pravdepodobnosti sa stáva, že ak je známa distribučná funkcia náhodnej premennej X, jej očakávaná hodnota je možné vypočítať - alebo matematickú nádej a (x) - a jej variačný var (x), pokiaľ tieto Existujú sumy. Recipročné však nemusia byť nevyhnutne pravdivé.

To znamená, že poznanie E (x) a var (x) nemusí nevyhnutne získať distribučnú funkciu x, takže množstvá ako p (| x |> k) pre niektoré k> 0 je veľmi ťažké získať. Ale vďaka Chbyshovovej nerovnosti je možné odhadnúť pravdepodobnosť náhodnej premennej.

Chbyshovova veta nám hovorí, že ak máme náhodnú premennú X na vzorkovom priestore s pravdepodobnostnou funkciou P a ak k> 0, potom:

Môže vám slúžiť: acutangle trojuholník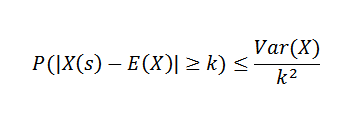

Aplikácie a príklady

Medzi mnohými aplikáciami, ktoré má Chbyshovova veta, je možné spomenúť:

1. Limit pravdepodobnosti

Toto je najbežnejšia aplikácia a používa sa na poskytnutie hornej úrovne pre p (| x-e (x) | ≥k), kde k> 0, iba s rozptylom a nádejou náhodnej premennej x, bez toho, aby som poznal funkciu pravdepodobnosti.

Príklad 1

Predpokladajme, že počet výrobkov vyrobených v spoločnosti za týždeň je náhodná premenná s priemerom 50.

Ak je známe, že rozptyl týždňa výroby sa rovná 25, potom čo môžeme povedať o pravdepodobnosti, že tento týždeň sa výroba líši o viac ako 10 do priemeru?

Riešenie

Aplikácia Chbyshovovho nerovnosti musíme:

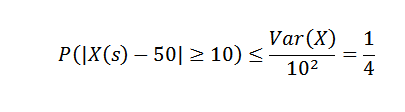
Z toho môžeme získať, že pravdepodobnosť, že vo výrobnom týždni je počet položiek presahovaný vo viac ako 10 do priemeru, je najviac 1/4.

2. Demonštrácia limitných teorémov

Chbyshovova nerovnosť zohráva dôležitú úlohu pri demonštrácii najdôležitejších limitov vety. Ako príklad máme:

Slabý zákon veľkého počtu

Tento zákon stanovuje, že vzhľadom na sukcesiu x1, x2, ..., xn, ... nezávislých náhodných premenných s rovnakým priemerným rozdelením E (xi) = μ a variant var (x) = σ², a známa priemerná vzorka:

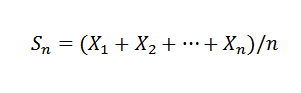
Takže pre k> 0 musíte:

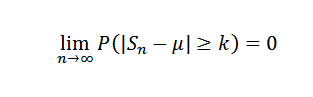
Alebo ekvivalent:

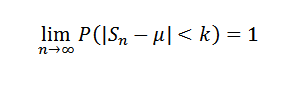
Demonštrácia

Najprv si všimneme nasledujúce:

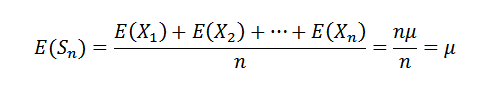
Keďže x1, x2, ..., xn sú nezávislé, z toho vyplýva, že:

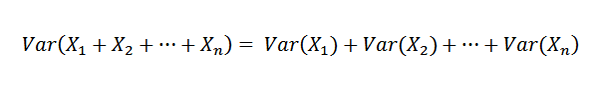
Preto je možné potvrdiť nasledujúce:

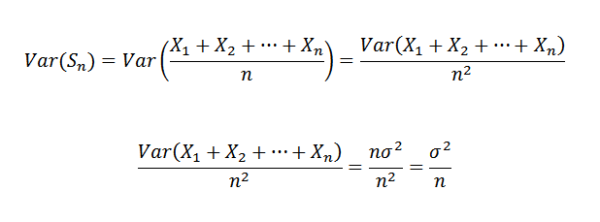
Potom pomocou Chbyshovovej vety musíte:

Môže vám slúžiť: trigonometrické funkcie: Základné, v karteziánskej rovine, príklady, cvičenie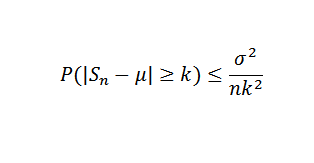

Nakoniec, veta je výsledkom skutočnosti, že správny limit je nula, keď N má tendenciu nekonečno.

Je potrebné poznamenať, že tento test sa vykonal iba pre prípad, v ktorom existuje rozptyl XI; to znamená, že sa nerozlišuje. Preto pozorujeme, že veta je vždy pravdivá, ak E (xi) existuje.

Chebyshovova limitná veta

Ak x1, x2, ..., xn, ... je to postupnosť nezávislých náhodných premenných tak, že existuje nejaké C0:

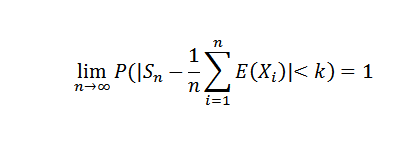
Demonštrácia

Pretože postupnosť odchýlok je rovnomerne obmedzená, máme var (sn) ≤ c/n, pre všetky prírodné n. Ale vieme to:

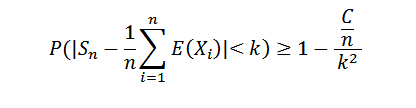
Vytváranie N do nekonečna je to nasledujúce:

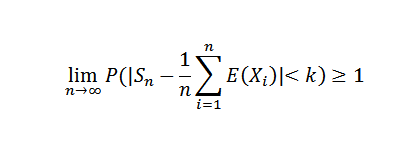
Pretože pravdepodobnosť nemôže prekročiť hodnotu 1, získaný požadovaný výsledok. V dôsledku tejto vety by sme mohli spomenúť konkrétny prípad Bernoulliho.

Ak sa experiment opakuje nezávisle s dvoma možnými výsledkami (zlyhanie a úspech), kde P je pravdepodobnosť úspechu v každom experimente a X je náhodná premenná, ktorá predstavuje počet získaných úspechov, potom pre každú k> 0 musíte:

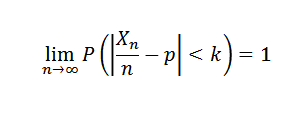
3. Veľkosť vzorky

Pokiaľ ide o rozptyl, nerovnosť Chbyshova nám umožňuje nájsť veľkosť vzorky, ktorá je dostatočná na to, aby sa zabezpečilo, že pravdepodobnosť, že | SN-μ |> = k je tak malá, ako je to potrebné, čo vám umožňuje mať prístup k priemer.

Presne, či už ide o x1, x2, ... xn vzorku nezávislých náhodných premenných s veľkosťou n a predpokladajme, že e (xi) = μ a jeho rozptyl σ². Takže kvôli Chbyshovovej nerovnosti musíte:

Môže vám slúžiť: číslo Eulera alebo číslo E: Koľko ok, vlastnosti, aplikácie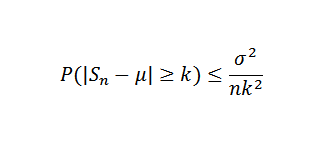

Teraz buďte δ> 0 pevné. Musíme:

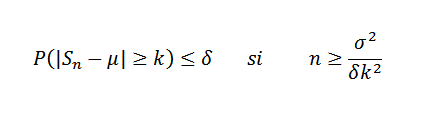
Príklad

Predpokladajme, že x1, x2, ... xn sú vzorka nezávislých náhodných premenných s distribúciou Bernoulli, takže berú hodnotu 1 s pravdepodobnosťou p = 0.5.

Aká by mala byť veľkosť vzorky, aby sa zabezpečilo, že pravdepodobnosť, že rozdiel medzi aritmetickým priemerom SN a jeho očakávanou hodnotou (ktorá presahuje viac ako 0,1), je menšia alebo rovná 0.,01?

Riešenie

Musíme (x) = μ = p = 0,5 a čo var (x) = σ²= P (1-P) = 0,25. Pre Chbyshovovu nerovnosť, pre každú k> 0 musíme:

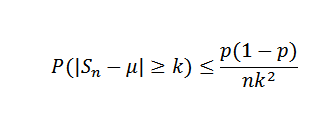
Teraz, keď vezmete k = 0,1 a δ = 0,01, musíte:

Týmto spôsobom sa dospelo k záveru, že je potrebná veľkosť vzorky najmenej 2500, aby sa zabezpečilo, že pravdepodobnosť udalosti | Sn - 0,5 |> = 0,1 je menšia ako 0,01.

Nerovnosti typu chebyshov

Existujú rôzne nerovnosti súvisiace s nerovnosťou Chbyshova. Jedným z najznámejších je Markovova nerovnosť:

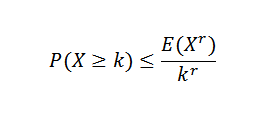
V tomto výraze x je to negatívna náhodná premenná s k, r> 0.

Markovova nerovnosť môže mať rôzne formy. Napríklad buď a negatívna náhodná premenná (takže p (y> = 0) = 1) a predpokladajme, že E (y) = μ existuje. Predpokladajme tiež, že (e (y))^r= μ_r Existuje celé číslo r> 1. Tak:

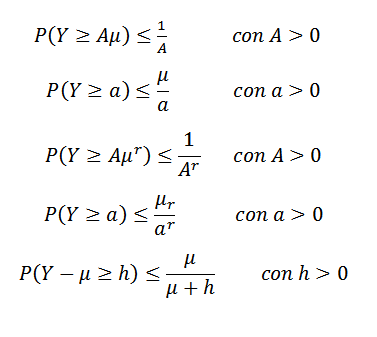
Ďalšou nerovnosťou je gauss, ktorá nám hovorí, že pri danej unimodálnej x náhodnej premennej s módou na nule, potom pre k> 0,