Bolzanská veta

Vysvetľujeme, čo je Bolzanova veta, jej aplikácie a vyriešené cvičenia

Čo je to Bolzanova veta?

On Bolzanská veta Uvádza sa, že ak je funkcia nepretržitá vo všetkých bodoch uzavretého intervalu [a, b] a je splnené, že obraz „a“ a „b“ (pod funkciou) má opačné príznaky, potom bude aspoň tu Jeden bod „C“ v otvorenom intervale (a, b), takže funkcia vyhodnotená v „c“ bude rovná 0.

Túto vetu uviedol v roku 1850 filozof, teológ a matematik Bernard Bolzano v roku 1850. Tento vedec, ktorý sa narodil v súčasnej Českej republike, bol jednou z prvých matematiky v histórii, ktorá vytvorila formálnu demonštráciu vlastností kontinuálnych funkcií.

Vysvetlenie vety

Bolzanova veta je známa aj ako veta medziproduktov, ktorá pomáha pri určovaní špecifických hodnôt, najmä nulov, určitých skutočných funkcií skutočnej premennej.

V danej funkcii f (x) pokračuje -to znamená, že f (a) a f (b) sú spojené krivkou-, kde f (a) je pod os x (je záporná) a f (b) nad osou X (je kladná) alebo naopak, bude na osi X reza f (c) bude sa rovnať 0.

Pri grafickej analýze Bolzanovej vety je známe, že pre akúkoľvek kontinuálnu funkciu F definovanú v intervale [a, b], kde f (a)_*F (b) je menší ako 0, v intervale bude aspoň jeden koreň „C“ tejto funkcie (a, b).

Táto veta nezaviedla počet bodov existujúcich v tomto otvorenom intervale, iba uvádza, že existuje najmenej 1 bod.

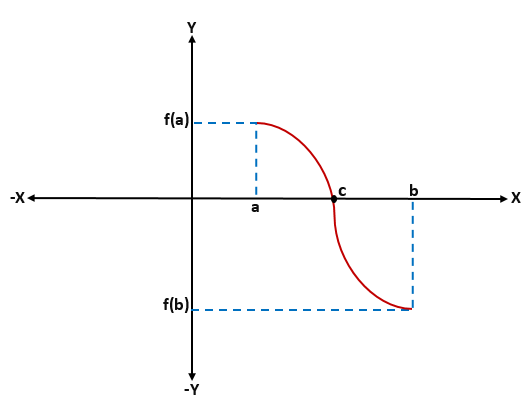
Demonštrácia Bolzano vety

Na demonštráciu Bolzanovej vety sa predpokladá bez straty všeobecnosti, že f (a) 0; Týmto spôsobom môže existovať veľa hodnôt medzi „a“ a „b“, pre ktoré f (x) = 0, ale je potrebné len preukázať, že existuje.

Môže vám slúžiť: imaginárne čísla: Vlastnosti, aplikácie, príklady

Začína sa hodnotiť f v strede (a+b)/2. Ak f ((a+b)/2) = 0, potom tu končí test; Inak je potom F ((a+b)/2) kladný alebo negatívny.

Jedna z polovíc intervalu [a, b] je vybraná tak, že príznaky funkcie vyhodnotené na koncoch sú rôzne. Tento nový interval bude [A1, B1].

Ak sa teraz vyhodnotilo v strede [A1, B1], nie je nula, potom sa rovnaká operácia vykonáva skôr; To znamená, že jedna polovica tohto intervalu, ktorá spĺňa stav príznakov, je vybraná. Je tento nový interval [A2, B2].

Ak tento proces pokračuje, potom sa uskutočnia dva úspechy an a bn, také, že:

an rastie a bn klesá:

A ≤ A1 ≤ A2 ≤ ... ≤ An ≤ .. . ≤ .. . ≤ bn ≤ .. . ≤ b2 ≤ b1 ≤ b.

Ak sa vypočíta dĺžka každého intervalu [AI, BI], budete musieť:

B1-A1 = (B-A)/2.

B2-A2 = (B-A)/2².

.. .

bn-an = (b-a)/2^n.

Preto je limit, keď N má tendenciu nekonečno (bn-an) rovná 0.

Použitie tohto an rastie a obmedzuje a bn klesá a obmedzuje, existuje hodnota „c“ taká, že:

A ≤ A1 ≤ A2 ≤ ... ≤ An ≤ .. .≤ C ≤ .. . ≤ bn ≤ .. . ≤ b2 ≤ b1 ≤ b.

LIM Limit je „C“ a limit bn je tiež „C“. Preto, vzhľadom na akýkoľvek Δ> 0, vždy existuje „n“ tak, že interval [an, bn] je obsiahnutý v intervale (C-ô, c+δ).

Teraz sa musí ukázať, že f (c) = 0.

Ak f (c)> 0, potom, keď je F súvislý, existuje ε> 0, takže f je pozitívny v celom intervale (c -ε, c+ε). Ako je však uvedené vyššie, existuje hodnota „N“ taká, že F sa zmení v [an, bn] a navyše [an, bn] je obsiahnuté v (c -kam, c+ε), čo je čo je rozpor.

Ak f (c) 0 tak, že f je v celom intervale negatívny (c -ε, c+ε); Existuje však hodnota „N“, ktorá sa zmení na prihlásenie v [an, bn]. Ukazuje sa, že [an, bn] je obsiahnutý v (c -ε, c+ε), čo je tiež protirečenie.

Môže vám slúžiť: Známky zoskupenia

Preto f (c) = 0 a to je to, čo chcelo byť preukázané.

Čo je to Bolzano veta pre?

Z jeho grafickej interpretácie sa Bolzanova veta používa na nájdenie koreňov alebo nulov v súvislej funkcii prostredníctvom bisenzie (prístup), čo je prírastková metóda vyhľadávania, ktorá vždy rozdeľuje intervaly do 2 do 2.

Ak teda funkcia zmení znamenie v intervale, funkcia F sa vyhodnotí v strede, čo je vyjadrené takto: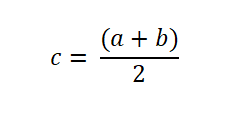Koreň sa nachádza, keď f (c) = 0. Ak nie, znak f (c) sa analyzuje, aby sa určilo, či je proti znaku F (a) alebo znaku f (b).

Potom sa uskutoční interval [a, c] alebo [c, b] tam, kde dôjde k zmene znaku a proces sa opakuje, až kým interval nie je menší, aby sa priblížil požadovanej hodnote; to znamená k hodnote, ktorú funkcia robí 0.

Stručne povedané, ak chcete uplatniť Bolzano vetu, a tak nájsť korene, obmedzte nuly funkcie alebo poskytnúť riešenie rovnici, vykonávajú sa nasledujúce kroky:

1. Overené, či F je kontinuálna funkcia v intervale [a, b].
2. Ak interval nie je uvedený, musíte nájsť takú, kde je funkcia nepretržitá.
3. Overuje sa, či konce intervalu dávajú opačné príznaky, keď sa hodnotia v f.
4. Ak sa nezískajú opačné príznaky, interval sa musí rozdeliť na dve subintervaly pomocou stredného bodu.
5. Vyhodnoťte funkciu v strede a overte, či je splnená hypotéza Bolzano, kde f (a) _* f (b) < 0.
6. V závislosti od znaku (kladnej alebo negatívnej) zistenej hodnoty sa proces opakuje s novým podintervalom, kým sa nesplní uvedená hypotéza.

Môže vám slúžiť: nelineárne programovanie: metódy a cvičenia

Vyriešené cvičenia

Cvičenie 1

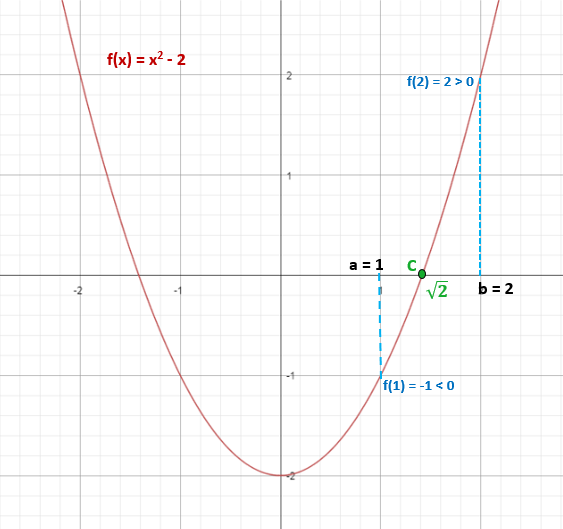
Určite, či funkcia f (x) = x² - 2, má v intervale aspoň jedno skutočné riešenie [1,2].

Riešenie

Máte funkciu f (x) = x² - 2. Rovnako ako polynóm, znamená to, že je v akomkoľvek intervale nepretržitý.

Žiada sa, aby sa zistilo, či má v intervale skutočné riešenie [1, 2], takže teraz musíte nahradiť iba konce intervalu vo funkcii, aby ste ich poznali a vedeli, či spĺňajú podmienku bytia iné:

f (x) = x² - 2

f (1) = 1² - 2 = -1 (negatívne)

f (2) = 2² - 2 = 2 (pozitívne)

Znak f (1) ≠ znamenie f (2).

To zaisťuje, že existuje aspoň jeden bod „C“, ktorý patrí do intervalu [1,2], v ktorom f (c) = 0.

V tomto prípade sa hodnota „C“ dá ľahko vypočítať takto:

X² - 2 = 0

x = ± √2.

Takže √2 ≈ 1,4 patrí do intervalu [1,2] a spĺňa, že f (√2) = 0.

Cvičenie 2

Preukázať, že rovnica x⁵ + x + 1 = 0 má aspoň jedno skutočné riešenie.

Riešenie

Najprv si všimneme, že f (x) = x⁵ + X + 1 je polynomiálna funkcia, čo znamená, že je kontinuálna vo všetkých reálnych číslach.

V tomto prípade nie je uvedený žiadny interval, takže si musíte vybrať hodnoty intuitívne, najlepšie blízko 0, aby ste vyhodnotili funkciu a našli zmeny znamienka:

Ak sa používa interval [0, 1], musí:

f (x) = x⁵ + x + 1.

f (0) = 0⁵ + 0 + 1 = 1> 0.

f (1) = 1⁵ + 1 + 1 = 3> 0.

Keďže nedôjde k zmene znakov, proces sa opakuje s iným intervalom.

Ak sa používa interval [-1, 0], musíte:

f (x) = x⁵ + x + 1.

f (-1) = (-1)⁵ + (-1) + 1 = -1 < 0.

f (0) = 0⁵ + 0 + 1 = 1> 0.

V tomto intervale dochádza k zmene nápisu: znamenie f (-1) ≠ znaku f (0), čo znamená, že funkcia f (x) = x⁵ + X + 1 má v intervale aspoň jeden skutočný koreň „C“, takže f (c) = 0. Inými slovami, je pravda, že x⁵ + X + 1 = 0 má v intervale skutočné riešenie [-1,0].