Bernoulli veta

Vysvetľujeme, čo je Bernoulliova veta, rovnice, aplikácie a riešenie cvičenia

Čo je Bernoulliho veta?

On Bernoulli veta Potvrdzuje, že v ideálnom kvapaline cirkulujúcom v potrubí je mechanická energia na jednotku objemu tekutiny konštantná vo všetkých častiach trubice, bez ohľadu na to, že majú odlišnú priečnu časť plochy a výšky.

Teraz je ideálna tekutina taká, ktorú nemožno stlačiť, takže jej hustota je pevná, bez ohľadu na tlakovú hodnotu.

Okrem toho má ideálna tekutina nulová viskozita, to znamená, že medzi tekutými vrstvami a ani medzi stenami potrubia neexistuje trenie.

Podmienky nestlačiteľnosti a nulovej viskozity sú nevyhnutné na uplatnenie Bernoulliho vety. Je tiež potrebné, aby bol tok stacionárny, to znamená, že tok sa v priebehu času nemení.

Na druhej strane, tok musí byť laminárny, takže počas priechodu potrubia nemôžu existovať žiadne vírenia alebo turbulencie.

Bernoulli rovnica

Rovnica Bernoulli má tri výrazy, práca vykonaná tlačou P, kinetickou energiou a energiou gravitačného potenciálu pre každú objemovú jednotku hustoty ρ ρ ρ

Bernoulliho rovnica je:

Na druhej strane rovnica kontinuity stanovuje, že v ideálnej tekutine je prietok konštantný vo všetkých častiach prietokovej trubice. To znamená, že objem tekutiny v rovnakej jednotke času je rovnaký vo všetkých častiach trubice.

Ak je tok q, potom:

Q = konštanta

S:

Q = A · V

Kde A je plocha prierezu trubice a V je rýchlosť tekutiny.

Môže vám slúžiť: umelé satelity

Poznamenáva, že v najužších častiach trubice musí tekutina cirkulovať rýchlejšie, pretože zostáva konštantná, aj keď sa mení. Preto je kinetická energia na jednotku objem väčšia.

Pretože Bernoulliho veta stanovuje, že mechanická energia je konštantná vo všetkých častiach, v užších častiach väčšej kinetickej energie, potenciálna energia klesá. 

Potenciálna energia pozostáva z gravitačnej energie na jednotku objemu plus práce vykonanú tlakom v jednotkovom objeme, a preto zníženie potenciálnej energie tiež znižuje tlak.

Stručne povedané, kombinovaný účinok princípu kontinuity a Bernoulliho veta vedie k úzkym častiam prietokovej trubice, kde je rýchlosť tekutiny väčšia, tlak klesá vzhľadom na širšie úseky.

Výrazy v rovnici Bernoulli

1) Práca vykonaná tlakom na jednotku objemu 

V časti prierezov oblasti až, Tekutina sa pohybuje množstvom siež, Kvôli tlaku p, ktorý vytvára silu f = plek a.

Práca vykonaná silou je:

Flek = plek A⋅ s

Pretože produkt A zajtra predstavuje vytlačený objem, práca vykonaná na jednotku objemu sa numericky zhoduje s hodnotou p v uvažovanej časti.

2) Kinetická energia jednotkového objemu tekutiny

Pretože tekutina je nestlačiteľná, jej hustota má pevnú hodnotu nazývanú ρ.

Keď sa tekutina cirkuluje cez prierez A, pohybuje sa množstvom v čase t, prietok je:

Môže vám slúžiť: Druhý zákon termodynamiky: vzorce, rovnice, príklady

v = s/t

A kinetická energia uvedenej časti tekutiny sa vypočíta podľa:

K = ½ ρ (a⋅s) v²

Ale ak je posunutý objem (Alek) jednotka, potom bude termín kinetickej energie daný ½ ρ V².

3) Gravitačný potenciál energie jednotkového objemu tekutiny vo výške h 

Pre časť cestnej kvapaliny m a výška h Pokiaľ ide o určitú referenčnú úroveň, gravitačná energia je daná:

U = m⋅ g⋅ h

Ak cesto m Zodpovedá jednotkovej časti tekutiny, potom sa hmotnosť porcie zhoduje s hustotou ρ, Takže potenciálna energia bude ρ⋅ g⋅ h.

Aplikácie Bernoulli Theorrem

Aerodynamická podpora

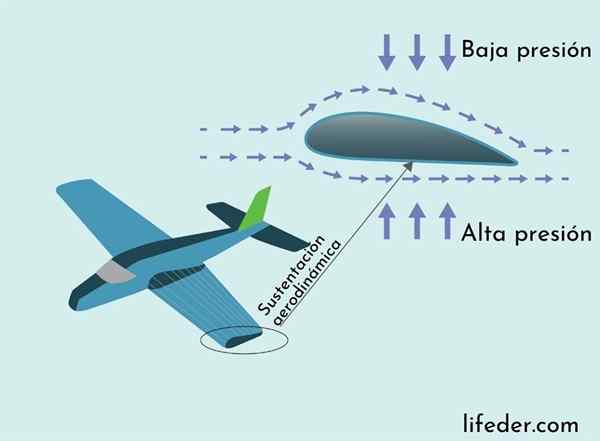Aerodynamickú podporu vysvetľuje Bernoulliho veta

Sila, ktorá zabraňuje letelu v lete na kolaps, je aerodynamická podporná sila. Čistá oporná sila je nasmerovaná vertikálne hore a pôsobí pozdĺž lietadlového krídla. Jeho pôvod je vysvetlený Bernoulliho vetou.

Krídlo lietadla má prierez s dlhšou krivkou na vrchu a kratšia na spodnej časti. Vďaka tomu je vzduchová trasa blízko povrchu krídla na vrchu, takže vzduch tečie rýchlejšie nad krídlom ako spodná časť. 

V dôsledku Bernoulliho vety je tlak vzduchu v hornej časti cirkulujúceho krídla menší ako na spodnej časti, čo vedie k tomu, že sil vidieť na nasledujúcom obrázku.

Môže vám slúžiť: fyzika počas Grékov (Antige Grécko)

Spustenie loptičiek a loptičiek s efektom krivky

V niektorých športoch, ako je futbal, baseball a Cricke, skúsení hráči vedia ako. Sa volá Efekt spustenia.

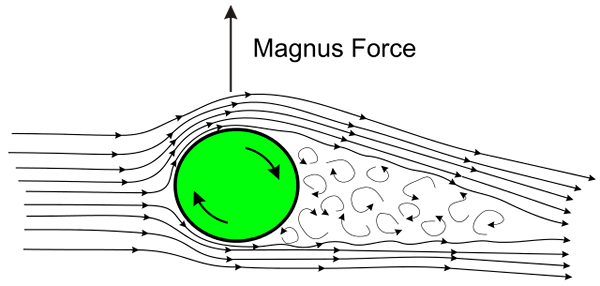Ilustrácia Magnus Effect. Zdroj: Wikimedia Commons

Účinok sa vyskytuje vždy, keď sa guľa alebo guľa rýchlo otáča pri pohybe vzduchom. Rotácia spôsobuje, že vzduch na povrch gule je ťahaný dvoma opačnými smermi, jeden v prospech smeru prekladu a na druhej strane proti smeru posunu.

V dôsledku vzduchového odporu sa na čele gule a na opačnej strane vyrába nízkotlaková oblasť.

Vysvetlenie tohto javu známeho ako Efekt Magnus Presne sa nachádza v Bernoulliho vete: kde tekutina cirkuluje rýchly tlak, je nízky a na strane, kde tlak cirkuluje pomaly pomaly.

Cvičenie

Horizontálna trubica má časť a časť a₁ = 40 štvorcových centimetrov a iná časť oddielu a₂ štyrikrát nižšie. Ak je prietok vody 6 l/s, určte rozdiel tlaku a výškový rozdiel vo vertikálnych skúmavkách.

Riešenie 

Počnúc tokovou rovnicou, ktorej hodnota je q = 6 l/s:

Q = A · V

Potom musíte rýchlosť v širokej časti 1,5 m/s av úzkom úseku 6 m/s.

Potom, pri nanášaní a porovnaní rovnice Bernoulliho na širokom a úzkom úseku, sa získa tlakový rozdiel 1700 PA, čo zodpovedá výškovému rozdielu vo zvislých skúmavkách 1,72 metra.