Súčet polynómov, ako sa to robí, príklady, cvičenia

Ten Súčet polynómov Je to operácia, ktorá spočíva v pridaní dvoch alebo viacerých polynómov, čo vedie k inému polynómu. Na jeho vykonanie je potrebné pridať podmienky rovnakého poradia každého z polynómov a uviesť výslednú sumu.

Najprv stručne preskúmame význam „podmienok toho istého poriadku“. Polynóm kohokoľvek spočíva v sumách a/alebo odčítaní podmienok.

postava 1. Na pridanie dvoch polynómov je potrebné ich objednať a potom znížiť podobné podmienky. Zdroj: Pixabay + Wikimedia Commons.

Podmienky môžu byť produktmi reálnych čísel a jednou alebo viacerými premennými, ktoré sú znázornené písmenami, napríklad: 3x² a -√5.do²Bc³ Sú to podmienky.

Podmienky toho istého poriadku sú tie, ktoré majú rovnaký exponent alebo moc, hoci môžu mať iný koeficient.

-Podmienky rovnakého poriadku sú: 5x³, √2 x³ a -1/2x³

-Rôzne objednávky Podmienky: -2x^-2, 2xy^-1 a √6x²a

Je dôležité mať na pamäti, že je možné pridať alebo odpočítať iba podmienky toho istého poriadku zníženie. Inak je súčet jednoducho uvedený.

Po objasnení pojmu pojmy toho istého poriadku sa polynómy pridávajú podľa týchto krokov:

-objednať Najprv polynómy, ktoré sa majú pridať rovnakým spôsobom, buď sa zvyšujú alebo klesajú, to znamená s právomocami od najmenej po najväčší alebo naopak.

-Dokončiť, V prípade, že chýba akýkoľvek výkon v sekvencii.

-Znížiť Podobné výrazy.

-Naznačovať Výsledná suma.

[TOC]

Príklady polynómu

Začneme pridaním dvoch polynómov s jednou premennou s názvom X, Napríklad polynómy p (x) a q (x) dané:

P (x) = 2x² - 5x⁴ + 2x -x⁵ - 3x³ +12

Q (x) = x⁵- 25 x + x²

Podľa opísaných krokov sa začína tak, že ich objednáva znížením, čo je najbežnejší spôsob:

P (x) = -x⁵- 5x⁴  - 3x³  + 2x² + 2x +12

Môže vám slúžiť: vpísaný uhol kruhu: definícia, vety, príklady

Q (x) = x⁵+ X² - 25x

Polynomial Q (x) nie je dokončený, je zrejmé, že právomoci s exponentom 4, 3 a 0. Ten je jednoducho nezávislý termín, ten, ktorý nemá žiadny list.

Q (x) = x⁵+ 0x⁴ + 0x³ + X² - 25x + 0

Akonáhle je tento krok hotový, sú pripravení pridať. Podobné výrazy môžete pridať a potom uviesť súčet alebo umiestniť polynómy objednané navzájom a znížiť stĺpcami týmto spôsobom:

- X⁵ - 5x⁴  - 3x³ + 2x² + 2x +12

+ X⁵ + 0x⁴ + 0x³  +  X²  - 25x + 0     +

--

0x⁵-5x⁴ - 3x³  +3x² - 23x + 12 = p (x) + q (x)

Je dôležité si uvedomiť, že pri pridaní sa to robí algebraicky rešpektujúc pravidlo znakov, týmto spôsobom 2x + (-25 x) = -23x. To znamená, že ak majú koeficienty odlišné znaky a výsledok nesie znak hlavného.

Pridajte dva alebo viac polynómov s viac ako jednou premennou

Pokiaľ ide o polynómy s viac ako jednou premennou, jedna z nich je vybraná na objednávku. Predpokladajme napríklad, že sa požaduje, aby sa pridal:

R (x, y) = 5x²  - 4y² +  8xy - 6y³ 

A:

T (x, y) = ½ x²- 6 rokov²  - 11xy + x³a

Jedna z premenných je vybraná, napríklad X na objednávku:

R (x, y) = 5x² +  8xy - 6y³  - 4y²

T (x, y) = + x³y + ½ x² - 11xy - 6y² 

Chýbajúce výrazy sú okamžite dokončené, podľa ktorých má každý polynóm:

R (x, y) = 0x³a + 5x² +  8xy - 6y³  - 4y²

T (x, y) = + x³y + ½ x² - 11xy + 0y³ - 6 rokov² 

A obaja sú pripravení znížiť podobné výrazy:

0x³a + 5x² +  8xy - 6y³  - 4y²

Môže vám slúžiť: určovací koeficient: vzorce, výpočet, interpretácia, príklady

+ X³y + ½ x² - 11xy + 0y³ - 6 rokov²       +

-

+ X³Y + 11/2x² - 3xy - 6³  - 10 y²    = R (x, y) + t (x, y)

Polynomiálne súčet

- Cvičenie 1

V ďalšom súčte polynómov uveďte termín, ktorý musí ísť do slepého bloku, aby sa získal polynomiálny súčet:

-5x⁴  + 0x³ +  2x²         + 1

X⁵  + 2x⁴             - 21x² + 8x - 3

2x⁵             +9x³             -14x

-

-6x⁵+10x⁴ -0x³  + 5x²   - 11x + 21

Riešenie

Na získanie -6x⁵ Vyžaduje sa termín formy sekery⁵, také:

A + 1+ 2 = -6

Preto:

A = -6-1-2 = -9

A požadovaný termín je:

-9x⁵

-Pokračujte podobným spôsobom, aby ste našli zvyšné podmienky. Tu je exponent 4:

-5 + 2 + A = 10 → A = 10 + 5-2 = 13

Chýbajúci termín je: 13x⁴.

-Pre X Svaly³ Je okamžité, že tento výraz musí byť -9x³, Týmto spôsobom je koeficient kubického pojmu 0.

-Pokiaľ ide o štvorcové právomoci: a + 8 -14 = -11 → a = -11 -8 + 14 = -5 a termín je -5x².

-Lineárny termín sa získava pomocou +8 -14 = -11 → A = -11 + 14 -8 = -5, čo je chýbajúci termín -5x.

-Nakoniec je nezávislý termín: 1 -3 + A = -21 → A = -19.

- Cvičenie 2

Plochý terén je obklopený tak, ako je to znázornené na obrázku. Nájdite výraz pre:

a) obvod a

b) jeho oblasť, pokiaľ ide o uvedené dĺžky:

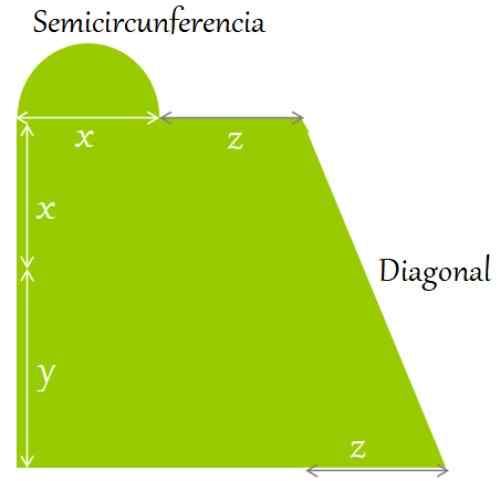Obrázok 2. Plochý terén je obklopený označeným formou a rozmermi. Zdroj: f. Zapata.

Roztok

Obvod je definovaný ako súčet bokov a obrysov obrázku. Začínajúc v ľavom dolnom rohu, v smere rúk hodín, máte:

Môže vám slúžiť: Isosceles lichobežník: vlastnosti, vzťahy a vzorce, príklady

Obvod = y + x + dĺžka polkruhu + z + diagonálna dĺžka + Z + z + x

Polkruh má priemer rovný x. Pretože polomer je polovica priemeru, musí:

Rádio = x/2.

Vzorec pre dĺžku úplného obvodu je:

L = 2π x rádio

Tak:

Dĺžka polkruhu = ½. 2π (x/2) = πx/2

Pokiaľ ide o svoju časť, diagonál sa vypočíta s vetou Pythagory aplikovanou na strany: (x+y), čo je zvislá strana a Z, čo je horizontálna: vodorovná:

Diagonálna = [(x+y)² + z²]^1/2

Tieto výrazy sa nahradia v obvode, aby sa získali:

Obvod = y + x + πx/2 + z + [(x + y)² + z²]^1/2+ z + x + z

Podobné výrazy sa znižujú, pretože suma vyžaduje, aby sa výsledok zjednodušila na maximum:

Obvod = y + [x + π (x/2) + x] + z + z + z + [(x + y)² + z²]^1/2 = y + (2 + π /2) x + 3z

Riešenie B

Výsledná oblasť je súčet oblasti obdĺžnika, polkruh a pravý trojuholník. Vzorce pre tieto oblasti sú:

-Obdĺžnik: Výška

-Polkruh: ½ π (rádio)²

-Trojuholník: Base X Výška /2

Obdĺžnik

(x+y). (x+z) = x² + Xz + yx + yz

Plocha

½ π (x/2)² = π x² / 8

Oblasť trojuholníka

½ z (x + y) = ½ zx + ½ zy

Celková plocha

Na nájdenie celkovej plochy sa pridajú výrazy nájdené pre každú čiastočnú oblasť:

Celková plocha = x² + Xz + yx + yz + (π x² / 8) + ½ zx + ½ zy

A nakoniec všetky výrazy, ktoré sú podobné:

Celková plocha = (1 + π/8) x² + 3/2 xy + 3/2yz + yx

Odkazy

1. Baldor, a. 1991. Algebra. Venezuelské kultúrne redaktory.Do.
2. Jiménez, r. 2008. Algebra. Sála.
3. Matematika je zábava. Polynómy pridávania a odčítania. Získané z: Mathsisfun.com.
4. Inštitút Monterey. Pridanie a odpočítavanie polynómov. Získané z: Montereyinstitute.orgán.
5. UC Berkeley. Algebra polynómov. Získané z: matematiky.Berkeley.Edu.