Sukcesia

Dedičstvo zložená zo žltých a modrých štvorcov. Zdroj: f. Zapata

Čo je to zložená sukcesia?

A sukcesia Skladá sa zo sekvencie prvkov, vytvorených z dvoch (alebo viacerých) rôznych a alternatívnych úspechov. Každá z týchto strán má konkrétne pravidlo, ktoré sa používa na nájdenie svojich príslušných prvkov.

Prvky nemusia byť číselné, sú schopné byť číslami, symbolmi alebo písmenami, ale tie, ktoré sú založené na číslach aritmetické úspechy. Obrázok, s ktorou začína náš článok, ukazuje zloženú postupnosť zo žltých a modrých štvorcov.

V tomto slede začína z veľkého štvorca pozostávajúce z 8 žltých štvorcov a modrého štvorca. Ak chcete získať nasledujúci termín, doľava alebo vpravo z prvého a tretieho radu štvorcov sa pridá žltý štvorec. Priestor, ktorý má za následok centrálny rad, je vyplnený modrým štvorcom.

Každá hodnota v sekvencii sa volá termín. Ak chcete nájsť piaty termín, musíte do pravej a tretej rady pridať žltý štvorec a modrý štvorec v druhom riadku:

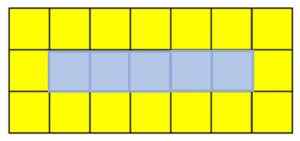Piaty termín sukcesie žltých a modrých štvorcov. Zdroj: f. Zapata

Vysvetlenie

Pri zložených úspechoch sa výrazy získajú striedaním podmienok dvoch alebo viacerých nezávislých jednoduchých scénických stránok. Aby sme lepšie porozumeli tejto myšlienke, malo by sa preskúmať podrobnosti o jednoduchej sukcesii.

Napríklad nasledujúca jednoduchá sukcesia pozostáva z prírodných čísel:

2, 4, 6, 8, 10, 12 ..

Podporné body naznačujú, že dedičstvo má nekonečné výrazy.

Každý z podmienok je označený malým písmenom a číslom, ako index. Toto číslo označuje pozíciu alebo index každého termínu. V predchádzajúcom slede môžete napísať:

do₁ = 2; do₂ = 4; do₃ = 6; do₄ = 8 ..

Je veľmi vhodné mať spôsob, ako vypočítať akýkoľvek termín, ktorý je požadovaný z dedenia, to znamená jeho konkrétne pravidlo. S ňou N-ésimo termín, ani Všeobecný, označený ako a_n.

Môže vám slúžiť: Vlastnosti rovnosti

Pokračovaním príkladu dedenia párnych čísel môžete z predchádzajúceho termínu stanoviť spôsob, ako vypočítať termín n-ésimo:

do_n = a_N-1 + 2

Kde_N-1 Je to termín, ktorý predchádza_n.

Samozrejme by bolo lepšie poznať všeobecný termín bez v závislosti od iných podmienok. V tomto slede je ľahké poznamenať, že akýkoľvek termín sa vynásobí 2 pozíciou, ktorú zaberá, vzhľadom na index termínu. Týmto spôsobom je napísaný:

do_n = 2n

Starí Gréci už poznali úspechy párne a nepárnych čísel. Postupnosť nepárnych prírodných čísel medzitým možno napísať ako:

1, 3, 5, 7, 9, 11 ..

A kombináciou postupnosti párnych čísel s nepárnymi, nasledujúca zložená sukcesia je:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 ..

Ktorého výsledkom je súbor prírodných čísel.

Podmienky zloženej sukcesie

Môže byť zábavné pokúsiť sa nájsť vzťah, ktorý existuje v poradí čísel, pre ktoré sa musí starostlivo pozorovať, a pokúsiť sa zistiť, či ide o zloženú sukcesiu.

Všeobecná forma sukcesie zloženej z dvoch stránok bude:

do₁, b₁, do₂, b₂, do₃, b₃, do₄, b₄,..

Kde₁, do₂, do₃, do₄,... sú podmienky prvej sukcesie a B₁, b₂, b₃, b₄,… Tí z druhého. Vždy sú rozptýlené, ako je to v tomto príklade:

7, 8, 14, 16, dvadsaťjeden, 24, 28, 32, 35..

Aký bude pojem, ktorý nasleduje?

Vedieť, poznať dedičstvo v dvoch alternatívnych množinách čísel nasledovne:

• 7, 14, 21, 28, 35 ..
• 8, 16, 24, 32 ..

V prvej z týchto súprav sa objavia násobky 7:

do₁ = 7 × 1 = 7; do₂ = 7 × 2 = 14; do₃ = 7 × 3 = 21; do₄ = 7 × 4 = 28; do₅ = 7 × 5 = 35

Všeobecné obdobie tejto sukcesie je:

do_n = 7n

A v druhom je to násobky 8:

b₁ = 8 × 1 = 8; b₂ = 8 × 2 = 16; b₃ = 8 × 3 = 24; b₄ = 8 × 4 = 32

Takže jeho všeobecný termín je:

Môže vám slúžiť: skutočná skutočná premenná funkcia a jej grafická reprezentácia

b_n = 8n

Po návrate k pôvodnej zloženej sukcesii patrí 35 do prvej sekvencie, ktorej pojmy sú₁, do₂, do₃, do₄ … 35 je piaty termín, takže nasledujúci výraz musí byť b₅, ktorý sa ľahko získa z pravidla na nájdenie všeobecného pojmu:

b₅ = 8 × 5 = 40

A je napísané:

7, 8, 14, 16, dvadsaťjeden, 24, 28, 32, 35, 40 ..

Príklady kompozitných úspechov

Príklad 1

Môžete si vytvoriť zloženú sukcesiu s geometrickými figúrkami, ako je štvorcový a kruh, ktorý ich usporiada, ako je to znázornené nižšie:

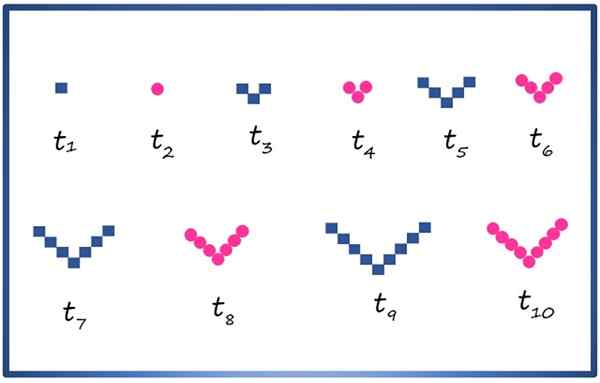Prvých 10 termínov zloženej sukcesie s štvorcovými geometrickými prvkami a kruhmi. Zdroj: f. Zapata

Každý termín je označený T₁, tón₂, tón₃, tón₄ …, Podmienky indexu Parque pozostávajú z kruhov a podmienok nepárneho indexu, štvorce. Starostlivo pozorovanie sekvencie je možné napríklad vedieť, že termín t_jedenásť, To sa neobjavuje na obrázku, pozostáva z 11 štvorcov s ustanovením vo V.

Príklad 2

Nasledujúca zložená sukcesia pozostáva zo symbolov, v tomto prípade listy R a S:

R ss rr sss rrr sss rrrr sss rrrr sssss ..

Každý nový termín je vytvorený pridaním listu k predchádzajúcemu. Prvé štyri výrazy zobrazenej sekvencie sú:

tón₁= R ; tón₂= H.H ; tón₃= Rr ; tón₄= SSS ..

A ďalší výraz, ktorý by sa objavil po uvedených podmienkach, je:

tón_jedenásť= Rrrrrr

Príklad 3

Predchádzajúce príklady ukázali stúpajúce úspechy, v ktorých každá hodnota sa nejakým spôsobom zvyšuje, pokiaľ ide o predchádzajúce. Ale nemusí to byť vždy takto, pretože úspechy môžu byť zostupné, to znamená, že majú zníženie vzoru.

A vzostupné úspechy možno kombinovať so zostupnými úspechmi.

Zkladá sa nasledujúca číselná sukcesia:

4, 36, 7, 35, 10, ___, ___, 33, 16, ___, ___, ..

Môže sa rozdeliť na dva scény:

• 4, 7, 10, ___, 16, ___, ..
• 36, 35, ___, 33, ___, ..

Aké sú hodnoty, ktoré musia byť umiestnené do prázdnych priestorov?

Starostlivo pozorovanie prvej sukcesie sa každý termín získa pridaním 3 do predchádzajúceho termínu. Je to preto vzostupná sukcesia:

Môže vám slúžiť: uhlové posunutie

7 = 4 + 3

10 = 7 + 3

Preto v prvom prázdnom priestore musíte umiestniť:

10 + 3 = 13

Potom je tento výraz v skutočnosti:

16 = 13 + 3

A ten, ktorý ide v druhom prázdnom mieste, je:

16 + 3 = 19

Druhá sukcesia klesá a je veľmi ľahké nájsť chýbajúce výrazy, pretože sa zistilo, že každý výraz sa získa odpočítaním 1 od predchádzajúceho termínu, preto:

36, 35, 3. 4, 33, 32..

Nakoniec môžete napísať:

4, 36, 7, 35, 10, 3. 4, 13, 33, 16, 32, 19,..

Vyriešené cvičenia

Cvičenie 1

V sukcesii zloženej z príkladu 3 v predchádzajúcej časti:

a) patrí 29 k uvedenej sukcesii?

b) Napíšte 10 ďalších podmienok tejto dedičstva

Odpovedať

Áno, patrí, pretože druhá sukcesia klesá a jeho podmienky sa získajú odpočítaním 1 od predchádzajúceho funkčného obdobia. Týmto spôsobom to nakoniec dosiahne 29.

Odpoveď B

4, 36, 7, 35, 10, 34, 13, 33, 16, 32, 19, 31, 22, 25, 29, 28, 31, 27, 34, ..

Upozorňujeme, že niektoré výrazy sa opakujú.

Cvičenie 2

Nájdite chýbajúce výrazy v nasledujúcom zloženom sukcesii:

100, 500, 115, 480, 130, 460, 145, 440, 160, 420, ..

Odpoveď

Čudné výrazy sú napísané na získanie prvej sukcesie:

100, 115, 130, 145, 160, ..

Zistilo sa, že na nájdenie každého termínu musíte pridať 15 k predchádzajúcemu termínu, preto pojem, ktorý nasleduje na 160, je 175.

Druhá sukcesia pozostáva z:

500, 480, 460, 440, 420, ..

Každý termín sa líši od predchádzajúceho do 20 rokov, vďaka čomu je postup, ktorý nasledoval pri 420, 400.

S týmito informáciami sa do pôvodnej zloženej sukcesie pridávajú ďalšie dva výrazy, ako je tento:

100, 500, 115, 480, 130, 460, 145, 440, 160, 420, 175, 400, ..

Odkazy

1. Larson, R. (2012). Predbežné vyfarbenie. 8. Vydanie. Učenie sa.
2. Stewart, J. (2007). Predbežné vycvičenie: matematika na výpočet. 5. Vydanie. Učenie sa.
3. Kompozitné úspechy. Obnovené z: médií.Vzdelávacie.Škriatok.mx.
4. Numerické úspechy. Zdroj: Matemathweb.com.
5. Úspechy. Aritmetické a geometrické progresie. Zdroj: Macmillaneducation.je.