Revolúcia Objem tuhých látok, typy, vyriešené cvičenia

On Revolúcia pevná Je to trojrozmerná postava, ktorá je generovaná rotáciou rovného povrchu okolo axiálnej osi alebo osi revolúcie. Obrázok 1 ukazuje animáciu tuhej revolúcie generovanej týmto spôsobom.

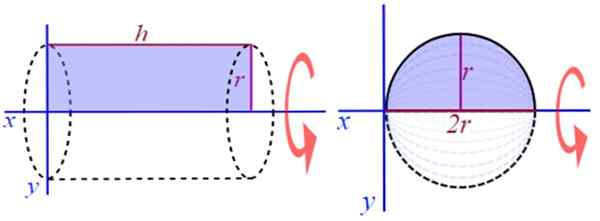
Ďalším veľmi ľahkým príkladom na vizualizáciu je generovanie priameho kruhového valca, ktorý otáča obdĺžnik výšky alebo dlhé H a rádio R, okolo osi kladného x (obrázok 2). Ak chcete nájsť svoj objem, je známy vzorec:

V = základná plocha x výška

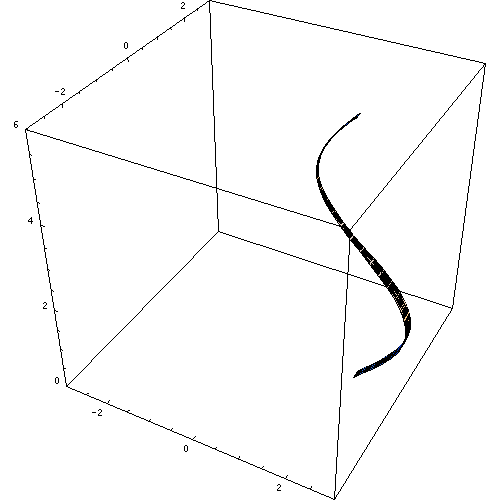postava 1. Obrázok generovaný rotáciou krivky Sen X. Zdroj: Wikimedia Commons. Macks/cc By-SA (https: // creativeCommons.Org/licencie/By-SA/2.5).

Ďalšie tuhé látky sú guľa, rovný kruhový kužeľ a rôzne čísla podľa povrchu umiestneného v rotácii a samozrejme, vybraná osi.

Obrázok 2. Generovanie priameho kruhového valca a gule. Zdroj: Wikimedia Commons.

Napríklad otáčanie polkruhu okolo čiary rovnobežného s priemerom sa získava tuhá revolúcia.

Pre valec, kužeľ, guľa, masívy a otvory, existujú vzorce na nájdenie objemu, ktorý závisí od polomeru a výšky. Ale ak je generovaný inými povrchmi, objem sa vypočíta pomocou definovaných integrálov.

[TOC]

Typy revolúcií pevných látok

Revolučné pevné látky možno klasifikovať podľa krivky, ktorá ich generuje:

Sféra

Stačí otočiť polkruh okolo osi, ktorý bude priemerom gule rádio R gule. Jeho hlasitosť je:

Vložka_sféra = (4/3) πr³

Kunda

Na získanie kužeľa H a rádio R, povrch, ktorý musí. Jeho hlasitosť je:

Vložka_Kunda = (1/3) πHr²

Valček

Otáčanie obdĺžnika okolo axiálnej osi, ktorá prechádza jednou stranou, ktorá môže byť krátkym alebo dlhou stranou, získa sa priamy kruhový val s polomerom R a výškou H, ktorého objem je:

Môže vám slúžiť: lano (geometria): dĺžka, veta a cvičenia

Vložka_valček = πr²H

Toroid

Býk má formu šišky. Získa sa rotáciou kruhovej oblasti okolo čiary v rovine, ktorá nepretína kruh. Jeho objem je daný:

Vložka_Toroid = 2πa²R

Kde A je polomer prierezu a R je polomer toroidu podľa schémy uvedenej na obrázku:

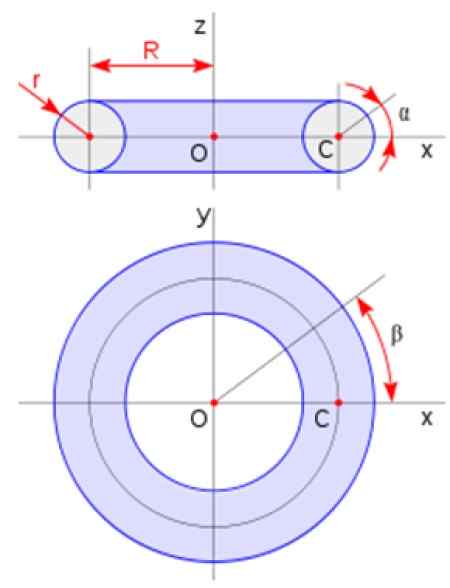Obrázok 3. Toroidné rozmery. Zdroj: Wikimedia Commons.

Metódy na výpočet objemu revolúcie pevné

Pri integrálnom výpočte sú tieto dve metódy časté:

-Disky a podložky

-Škrupina

Metóda diskov alebo podložky

Keď plátok revolúcie, prierez môže byť albumom, ak je tuhá látka alebo môže byť druh podložky (album s otvorom v strede), ak je to pevná diera.

Predpokladajme, že okolo horizontálnej osi sa otáča plochá oblasť. Z tejto plochej oblasti berieme malý obdĺžnik šírky AX, ktorý sa otáča kolmo okolo axiálnej osi.

Výška obdĺžnika je medzi najvzdialenejšou krivkou r (x) a najtlaškom najnadnejším r (x). Zodpovedajú vonkajšiemu polomeru a vnútornému rádiu.

Pri tejto rotácii sa generuje podložka objemu AV, daná:

ΔV = úplný objem - objem otvorov (ak existuje)

Pamätajte, že objem rovného kruhového valca je π. rozhlas² x výška, máme:

ΔV = π [r²(x) - r²(x)] δx

Pevná látka sa dá rozdeliť na množstvo malých častí objemu ΔV. Ak ich všetky pridáme, budeme mať celý objem.

Aby sme to dosiahli, budeme mať tendenciu k 0 objem ΔV, ktorý sa tiež stáva veľmi malým, a stane sa diferenciálom DX.

Môže vám slúžiť: vzájomne neexkluzívne udalosti: Vlastnosti a príklady

Máme teda integrál:

V = ∫_do^b π [r²(x) - r²(x)] dx

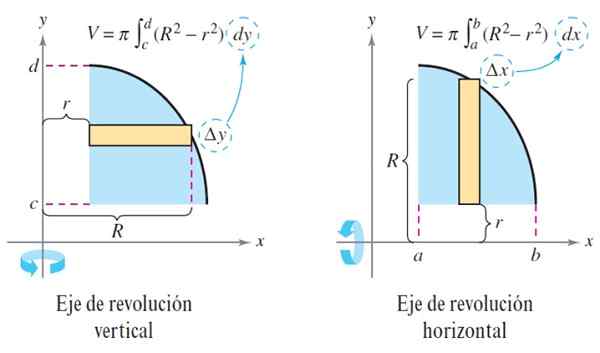Obrázok 3. Podložka. Zdroj: Larson. R. Kalkulácia.

V prípade, že je tuhá látka pevná, potom funkcia r (x) = 0, plátok generovanej tuhej látky je disk a objem zostáva:

V = ∫_do^b πr²x) dx

Keď je os revolúcie vertikálna, predchádzajúce rovnice majú formu:

V = ∫_do^b π [r² (Y) - r² (y)] dy a v = ∫_do^b πr²(Y) Dy

Vrstviť

Ako uvádza názov, táto metóda má predpokladať, že tuhá látka sa skladá z diferenciálnych hrubých vrstiev. Vrstva je tenká trubica, ktorá pochádza od otočenia obdĺžnika paralelne s osou rotácie.

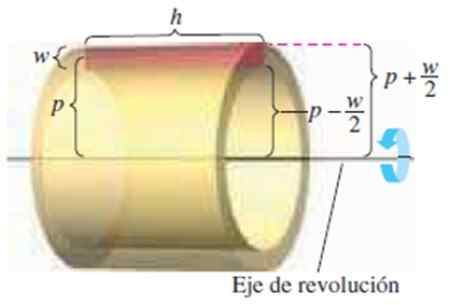Obrázok 4. Valcová vrstva výšky 2, dlhá H a polomer P. Zdroj: Larson, r. Kalkulácia.

Máme nasledujúce rozmery:

-Výška obdĺžnika W

-Jeho dĺžka h

-Vzdialenosť od stredu obdĺžnika k osi rotácie p

S vedomím, že objem vrstvy je Vonkajší objem - vnútorný objem:

π (p + w/2)²H - π (p - w/2)²h

Pri vývoji pozoruhodných výrobkov a zjednodušenie sa získa:

Objem vrstvy = 2π⋅p)WH

Teraz urobme výšku w obdĺžnika Δy, ako je vidieť na nasledujúcom obrázku:

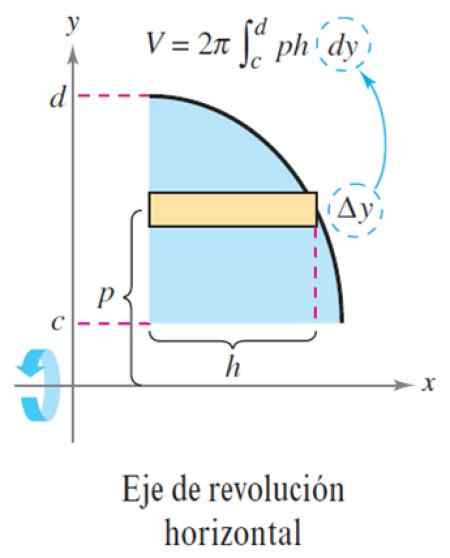Obrázok 5. Metóda vrstiev osi horizontálnej revolúcie. Zdroj: Larson, r. Výpočet premennej.

S tým je objem ΔV:

ΔV = 2π p x h x Δy

A výroba počtu vrstiev n Buďte veľmi veľkí, Δy sa stáva diferenciálnym farbám, takže celkový objem je neoddeliteľnou súčasťou:

V = ∫_c^d 2π p (y) h (y) dy

Opísaný postup sa uplatňuje podobne, keď je os revolúcie zvislá:

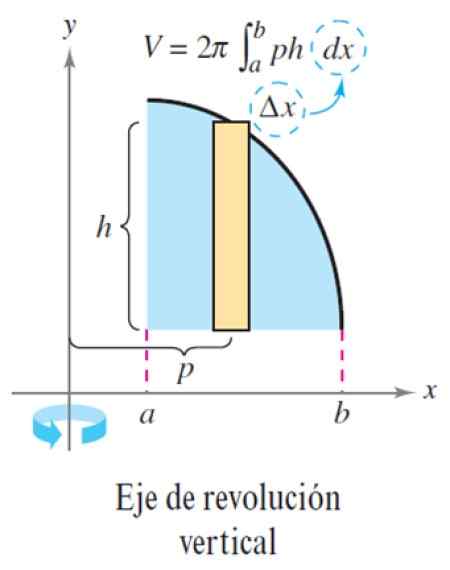Obrázok 6. Metóda vrstvy pre vertikálnu revolúciu. Zdroj: Larson, r. Výpočet premennej.

Cvičenie

Nájdite objem generovaný rotáciou plochej oblasti medzi krivkami:

y = x²;  y = 0; x = 2

Okolo osi a.

Môže vám slúžiť: negatívna homotecia

Riešenie

-Prvá vec, ktorú treba urobiť, je graf regiónu, ktorý vygeneruje revolúciu pevnú a poukazuje na os odbočky. Máme to v nasledujúcom grafe:

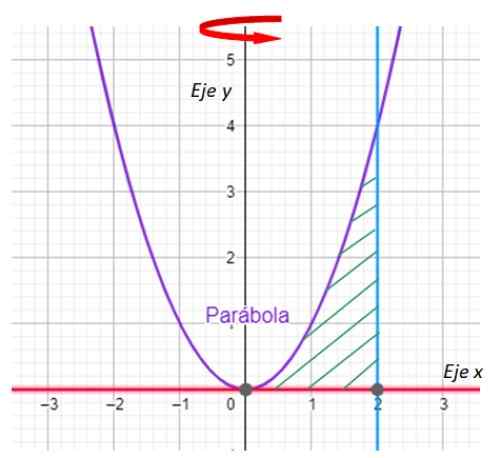Obrázok 7. Graf kriviek pre cvičenie vyriešené. Zdroj: f. Zapata s geogebou.

-Teraz sa hľadajú križovatky medzi krivkou y = x² a riadok x = 2. Z jeho časti Čiara y = 0 nie je nič iné ako os x.

Je ľahké varovať, že sa podobenstvo a čiara pretína v bode (2,4), čo je potvrdené nahradením x = 2 na y = x².

-Potom je zvolená jedna z metód na výpočet objemu, napríklad metóda vrstvy s vertikálnou osou revolúcie:

V = ∫_do^b 2π p (x) h (x) dx

Krok 1: Nakreslite obdĺžnik

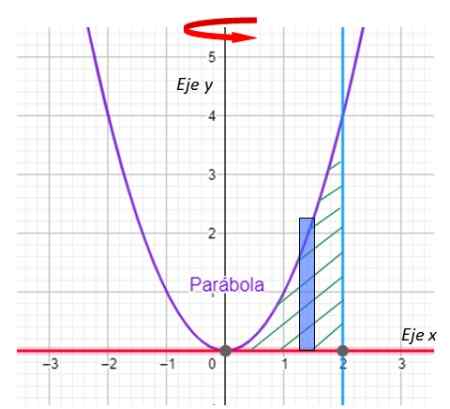Obrázok 8. Obdĺžnik pre vyriešený príklad. Zdroj: f. Zapata s geogebou.

Dôležité: V metóde vrstvy je dlhá strana obdĺžnika rovnobežná s osou rotácie.

Krok 2: Stanovte p (x)

Vrstva vrstvy je X

Krok 3: Stanovte H (x)

Výška obdĺžnika je určená podobenstvom x².

Krok 4: Zistite a vyriešte integrál objemu

Integračná premenná je x, ktorá sa pohybuje medzi 0 a 2, s tým máme limity integrácie. Výmena výrazov pre p (x) a h (x)

 Niektoré cvičenia môžu byť vyriešené oboma metódami. Môže to čitateľ vyriešiť metódou podložiek?

Odkazy

1. Larson, R. 2010. Výpočet premennej. 9NA. Vydanie. McGraw Hill.
2. Purcell, e. 2007. Výpočet analytickou geometriou. 9NA. Vydanie. Pearson Vzdelanie.
3. Wikipedia. Pevná revolúcia. Zdroj: In.Wikipedia.orgán.
4. Wikipedia. Toroid. Obnovené z: je.Wikipedia.orgán.
5. Wolfram Mathworld. Pevná revolúcia. Obnovené z: Mathworld.Valfram.com.