Oktál

Čo je osmičkový systém?

On Oktál Je to základný systém číslovania osem (8); To znamená, že pozostáva z ôsmich číslic, ktoré sú: 0, 1, 2, 3, 4, 5, 6 a 7. Preto každá číslica osmičkového čísla môže mať akúkoľvek hodnotu od 0 do 7. Octálne čísla sa tvoria z binárnych čísel.

Je to preto, že jej základňa je presnou silou dvoch (2). To znamená, že čísla, ktoré patria do oktálneho systému.

História oktálneho systému

Octálny systém má svoj pôvod v staroveku, keď ľudia používali ruky na spočítanie osem osem zvierat.

Napríklad, aby sa spočítal počet kráv v stajni, pravá ruka začala mať palec s malým prstom; Potom, aby ste spočítali druhé zviera, palec sa spojil s ukazovákom a tak ďalej so zvyšnými prstami každej ruky, až kým nedokončí 8.

Existuje možnosť, že systém oktálneho číslovania pred desatinným miestom, aby mohol spočítať interdigitálne priestory; to znamená, povedzte všetkým prstom, s výnimkou palcov.

Následne bol zavedený systém oktálneho číslovania, ktorý pochádza z binárneho systému, pretože potrebuje veľa číslic, aby predstavoval iba jedno číslo; Odvtedy boli vytvorené oktálové a šesťuholníkové systémy, ktoré nevyžadujú toľko číslic a ktoré sa môžu ľahko previesť na binárny systém.

Októbový systém číslovania

Octálny systém pozostáva z ôsmich číslic v rozmedzí od 0 do 7. Majú rovnakú hodnotu ako v prípade desatinného systému, ale ich relatívna hodnota sa mení v závislosti od polohy, ktorú títo zaberajú. Hodnota každej polohy je daná základnými právomocami 8.

Môže vám slúžiť: Pravidlo T: Charakteristiky, takže je to príklady

Polohy číslic v osmičkovom čísle majú nasledujúce pesos:

8⁴, 8³, 8², 8¹, 8⁰, Osemdesiet, 8^-1, 8^-2, 8^-3, 8^-4, 8^-5.

Hlavná osemtálna číslica je 7; Týmto spôsobom, keď sa v tomto systéme spočítajú, poloha číslice od 0 do 7 sa zvyšuje. Keď dosiahne 7, recykluje sa na 0 pre ďalší počet; To zvyšuje nasledujúcu pozíciu číslic. Napríklad na spočítanie sekvencií, v oktálnom systéme to bude:

• 0, 1, 2, 3, 4, 5, 6, 7, 10.
• 53, 54, 55, 56, 57, 60.
• 375, 376, 377, 400.

Existuje základná veta, ktorá sa uplatňuje na oktálový systém a je vyjadrená takto:

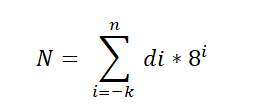
V tomto expresii DI predstavuje číslicu vynásobenú výkonom základnej 8, ktorá označuje polohovú hodnotu každej číslice, rovnakým spôsobom, ako je usporiadaný v desatinnom systéme.

Napríklad máte číslo 543.2. Aby sme to vzali do oktálneho systému, rozkladá sa takto:

N = ∑ [(5 _* 8²) + (4 _* 8¹) + (3 _*8⁰) + (2 _*8^-1)] = (5 * 64) + (4 * 8) + (2 * 1) + (2 * 0,125)

N = 320 +32 + 2 + 0,25 = 354 + 0,25_d

Týmto spôsobom máte 543.2_Otázka = 354,25_d. Dolný index, ktorý naznačuje, že je to oktálne číslo, ktoré môže byť tiež reprezentované číslom 8; a dolný index D sa vzťahuje na desatinné číslo, ktoré môže byť tiež reprezentované s číslom 10.

Konverzia osmičového systému na desatinné miesto

Aby sa previedol číslo oktálneho systému na svoj ekvivalent do desatinného systému, každá osmičková číslica sa musí vynásobiť jeho polohou, počnúc doprava.

Príklad 1

732₈ = (7_* 8²) + (3_* 8¹) + (2_* 8⁰) = (7 _* 64) + (3 _* 8) + (2 _* 1)

732₈= 448 +24 +2

732₈= 474₁₀

Môže vám slúžiť: matematická rovnosť

Príklad 2

26.9₈ = (2 _*8¹) + (6_* 8⁰) + (9_* 8^-1) = (2 _* 8) + (6 _* 1) + (9 _* 0,125)

26.9₈ = 16 + 6 + 1,125

26.9₈= 23,125₁₀

Konverzia desatinného systému na oktál

Celé číslo desatinného čísla sa môže previesť na osmičkové číslo pomocou metódy opakovaného delenia, kde je desatinné celé číslo rozdelené 8, kým sa kvocient rovná 0 a odpad každého delenia bude predstavovať osvopové číslo.

Odpad je objednaný od posledného po prvý; to znamená, že prvý zvyšok bude najmenej významnou číslicou oktálnej čísla. Týmto spôsobom bude najvýznamnejšou číslicou posledný zvyšok.

Príklad

Oktál z desatinného čísla 266₁₀

- Decimálne číslo 266 je vydelené 8 = 266/8 = 33 + 2 zvyšky.

- Potom je 33 vydelený 8 = 33/8 = 4 + 1 zvyšok.

- 4 je vydelený 8 = 4/8 = 0 + 4 zvyšky.

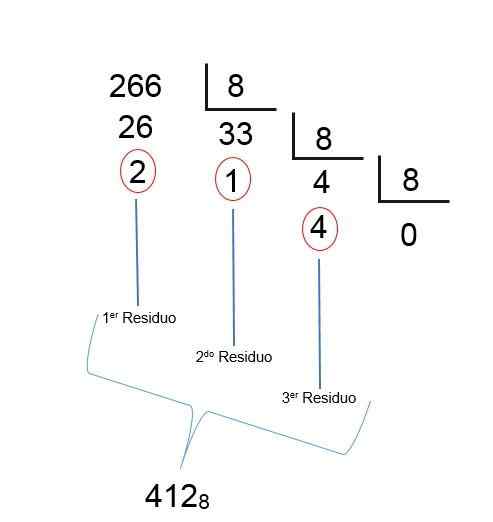
Rovnako ako pri poslednej divízii sa získa kvocient menší ako 1, znamená to, že výsledok bol nájdený; Iba pozostatky sa musia objednať naopak, takže oktálový počet desatinných miest 266 je 412, ako je vidieť na nasledujúcom obrázku:

Konverzia binárneho oktálneho systému

Konverzia oktálneho na binárny systém sa vykonáva pri konverzii osmičkovej číslice na svoju ekvivalentnú binárnu číslicu, tvorenú tromi číslicami. Existuje tabuľka, ktorá ukazuje, ako sa stáva osem možných číslic:

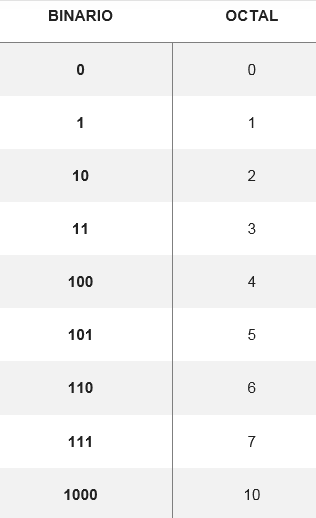
Z týchto konverzií môžete zmeniť ľubovoľný počet osmičkového systému na binárny, napríklad previesť číslo 572₈ Vaše ekvivalenty sú hľadané v stole. Preto musíte:

5₈ = 101

7₈= 111

2₈ = 10

Preto 572₈ ekvivalent v binárnom systéme do roku 10111110.

Binárny systém na osemtálnu konverziu

Proces konverzie integrálnych čísel na oktálne celé čísla je spätnou činnosťou predchádzajúceho procesu.

Môže vám slúžiť: Aké sú prvky uhla?

To znamená, že binárne čísla sú zoskupené do dvoch skupín po troch bitoch, počnúc sprava doľava. Potom sa s predchádzajúcou tabuľkou uskutoční binárna konverzia na oktál.

V niektorých prípadoch nebude mať binárne číslo skupiny 3 bitov; Na jeho dokončenie sa doľava od prvej skupiny pridá jeden alebo dva nuly.

Napríklad zmena binárneho čísla 11010110 na oktál sa vykoná nasledujúce:

- Skupiny 3 bitov sa vytvárajú začínajúce napravo (posledný bit):

11010110

- Pretože prvá skupina je neúplná, doľava sa pridá nula:

011010110

- Konverzia sa uskutoční z tabuľky:

011 = 3

010 = 2

110 = 6

Týmto spôsobom je binárne číslo 011010110 rovnocenné s 326₈.

Konverzia oktálneho systému na hexadecimálne a naopak

Ak chcete zmeniť osmičkové číslo na hexadecimálny alebo hexadecimálny na oktál, je potrebné, aby bolo toto číslo najprv binárne a potom do požadovaného systému.

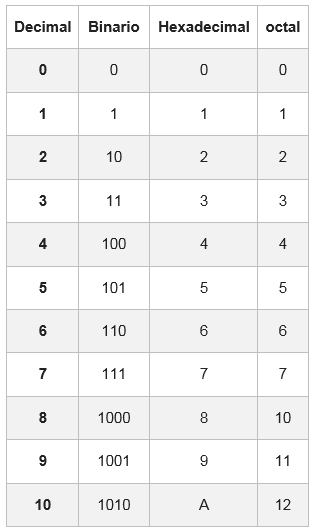
Z tohto dôvodu je tabuľka, v ktorej je každá hexadecimálna číslica reprezentovaná s jej rovnocennosťou v binárnom systéme, zloženom zo štyroch číslic.

V niektorých prípadoch nebude mať binárne číslo skupiny 4 bity; Na jeho dokončenie sa doľava od prvej skupiny pridá jeden alebo dva nuly

Príklad

Previesť oktálne číslo 1646 na hexadecimálne číslo:

- Octálne až binárne číslo sa stáva

1₈ = 1

6₈ = 110

4₈ = 100

6₈ = 110

- Preto 1646₈ = 1110100110.

- Aby sa obrátili z binárneho na hexadecimal, sú najprv usporiadané v skupine 4 bitov, počnúc doprava doľava:

11 1010 0110

- Prvá skupina je dokončená s nulami, takže môže mať 4 bity:

0011 1010 0110

- Uskutočňuje sa konverzia hexadeciálneho binárneho systému. Ekvivalencie sa nahradia pomocou tabuľky:

0011 = 3

1010 = a

0110 = 6

Týmto spôsobom je 1646 oktálna časť ekvivalentné 3A6 v hexadecimálnom systéme.