Obdĺžnikový súradnicový systém

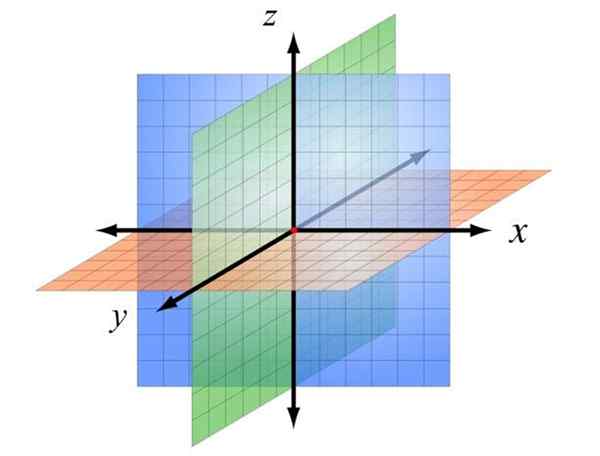
Karteziánsky súradnicový systém v troch rozmeroch. Zdroj: Wikimedia Commons

Čo je obdĺžnikový súradnicový systém?

V matematike a geometrii, a obdĺžnikový súradnicový systém Slúži na presné lokalizáciu akéhokoľvek bodu v priestore. Za to stačí dať tri súradnice.

Konštrukcia systému v rovine je veľmi jednoduchá, sú potrebné iba tri riadky, ktoré budú súradnicové osi alebo karteziánske sekery: jeden zvislý, ďalší vodorovný a tretí, ktorý vstupuje alebo opustí papier alebo obrazovku.

Tieto osi sú vzájomne kolmé a bod priesečníka je pôvod systém.

Toto ustanovenie je znázornené na obrázku vyššie, v ktorom boli písmená priradené listom X, a, z, rozlíšiť ich. Týmto spôsobom sú určené tri lietadlá, pričom pôvod je zafarbený červenou farbou.

Lietadlo Xz, V modrej farbe je rovina obrazovky a je pred očami čitateľa. Lietadlo Xy Je oranžový a môže byť spojený so stolom alebo podlahou. Nakoniec lietadlo šťavnatý V zelenej je kolmá na predchádzajúce a oddielu obrazovky alebo papier v dvoch regiónoch.

Kadrikulácia každého z týchto lietadiel a priradenie stupnice môžete uviesť akýkoľvek bod v priestore, ktorý dáva príslušným súradniciam X a z, Vždy v tomto poradí, aby sa predišlo nejasnostiam.

PrečoSlúži obdĺžnikovému súradnicovému systému?

Obdĺžnikový súradnicový systém slúži na umiestnenie akéhokoľvek bodu v priestore alebo v rovine, dosť na označenie troch súradníc bodu v poradí x, y, z.

Môže vám slúžiť: nominálna premenná: koncept a príklady

Ak bod patrí do roviny, jedna z súradníc bude 0 a ak je na ktorejkoľvek zo osí, dva z súradníc budú 0, s výnimkou toho, že zodpovedajúca umiestneniu bodu, s výnimkou pôvodu, čo, ako, ako Predtým povedal súradnice (0,0,0).

Nasledujúce príklady objasňujú vyššie uvedené.

Príklady

Príklad 1

Akýkoľvek bod P na osi x je vyjadrený prostredníctvom súradníc P (x, 0, 0). Všimnite si, že pôvod, zvýraznený červenou na nasledujúcom obrázku, má súradnice alebo (0, 0, 0).

Ak je bod napravo od pôvodu, má kladnú X súradnicu, zatiaľ čo ak je vľavo, je negatívny. Napríklad P1 Blue Point má súradnice (6,0,0), zatiaľ čo bod P2 v zelenej farbe má súradnice (-9,0,0).

Príklad 2

Na nasledujúcom obrázku sú dve osi, ktoré sú X os x vodorovná os a Os y Vertikálny. S tým stačí reprezentovať body v lietadle, pričom dve súradnice sú potrebné. Pôvod alebo je bod (0,0).

Všimnite si, že dispozícia osí rozdeľuje rovinu do štyroch oblastí nazývaných kvadranty. Osy vyššie a napravo od pôvodu sú označené pozitívnym znakom, zatiaľ čo dole a naľavo sa rozlišujú s negatívnym znakom.

Potom body, ktorých súradnice sú pozitívne, zodpovedajú prvému kvadrantu alebo kvadrantu i. Green Point má súradnice (2,3) a je v kvadrante i.

Pokiaľ ide o svoju časť, Red Point má súradnice (-3,1) a je v kvadrante II, zatiaľ čo súradnice modrého bodu sú (-1.5; -2.5) A je v kvadrante III.

Môže vám slúžiť: spoločná faktorizácia: príklady a cvičenia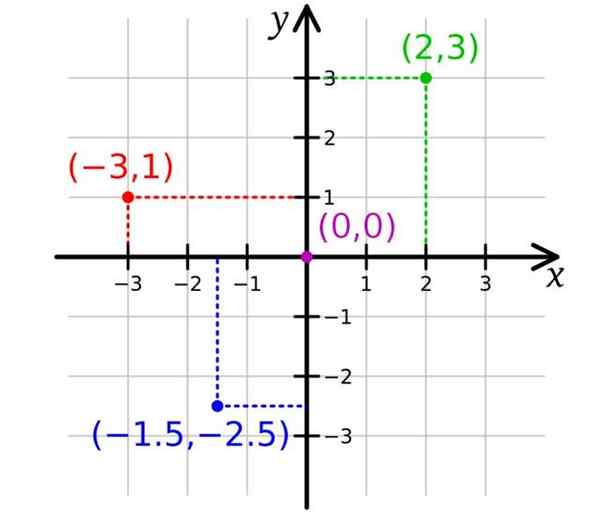 Karteziánska rovina. Zdroj: Wikimedia Commons

Príklad 3

Nasleduje príklad bodu vo vesmíre. Jeho súradnice sú x = 6, y = 10 a z = 8, preto P (6,10,8).

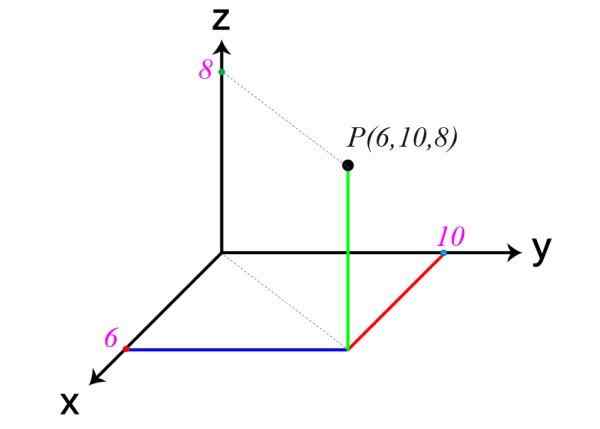Ďalší príklad karteziánskych osí

Na začiatku je varované, že plány XY, XZ a ZY rozdeľujú priestor na osem regiónov, nazývaných Oktavery. Bod p príkladu je v prvom ocante.

Odkazy

1. Alexander, D. (2013). Geometria. 5. Vydanie. Učenie sa.
2. Larson, R. (2012). Predbežné vyfarbenie. 8. Vydanie. Učenie sa.
3. Stewart, J. (2007). Predbežné vycvičenie: matematika na výpočet. 5. Vydanie. Učenie sa.
4. Karteziánske lietadlo. Zdroj: DL.Uncw.Edu.
5. Weisstein, e. Karteziánske súradnice. Obnovené z: Mathworld.Valfram.com