Centrálne vlastnosti symetrie, príklady a cvičenia

Dva body a a 'majú centrálna symetria Pokiaľ ide o bod alebo keď segment AA „prechádza ním a je tiež stredom AA“. Do tej miery alebo sa volá Stredisko symetrie.

Centrálna symetrika trojuholníka ABC vzhľadom na jeden bod alebo je ďalším trojuholníkom A'B'C ', ktorý má nasledujúce charakteristiky:

-Homológne segmenty majú rovnakú dĺžku 

-Ich zodpovedajúce uhly majú rovnaké opatrenie.

postava 1. ABC Triangle a jeho symetrický a'b'c '. Zdroj: f. Zapata.

Na obrázku 1 trojuholník ABC (červená) a jeho centrálna symetrická A'B'c '(zelená), vzhľadom na stred symetrie alebo. 

Na tom istom čísle by si pozorný pozorovateľ uvedomil, že rovnaký výsledok sa získa použitím pôvodnej rotácie trojuholníka, pokiaľ je 180 ° a zameraný na OR.

Preto je centrálna symetria rovnocenná s otočením o 180 ° vzhľadom na stred symetrie.

[TOC]

Vlastnosti centrálnej symetrie

Centrálna symetria má nasledujúce vlastnosti:

-Centrum symetrie je stredom segmentu, ktorý sa spája s jeho symetrickým.

-Symetrický bod iného, ​​ktorý sa nachádza v centre symetrie, sa zhoduje so stredom symetrie.

-Centrálnou symetrickou trojuholníka je zhodný trojuholník (rovnaký) ako originál.

-Obraz centrálnou symetriou obvodu je ďalším obvodom rovnakého polomeru.

-Kruh má centrálnu symetriu vzhľadom na svoje vlastné centrum.

Obrázok 2. Dizajn s centrálnou symetriou. Zdroj: Pixabay.

-Ellips má centrálnu symetriu vzhľadom na jej centrum.

-Segment má centrálnu symetriu vzhľadom na jeho stredný bod.

-Equilaterálny trojuholník nemá žiadnu centrálnu symetriu vzhľadom na jeho centrum, pretože jeho symetrická, aj keď zhodná s prvým, dáva ELILOLATERAL TRIAGLE obrátený.

Môže vám slúžiť: y = 3sen (4x) funkčné obdobie

-Štvorce majú centrálnu symetriu vzhľadom na ich centrum.

-Pentagón nemá ústrednú symetriu vzhľadom na jeho centrum.

-Pravidelné polygóny majú centrálnu symetriu, keď majú niekoľko strán krútiaceho momentu.

Príklady

Kritériá symetrie majú veľa aplikácií vo vede a inžinierstve. Centrálna symetria je prítomná v prírode, napríklad ľadové kryštály a pavučiny majú tento druh symetrie.

Okrem toho sa veľa problémov ľahko vyrieši, keď sa používa existencia centrálnej symetrie a iných druhov symetrie. Preto je vhodné rýchlo sa identifikovať, keď sa vyskytne.

Obrázok 3. Ľadové kryštály majú centrálnu symetriu. Zdroj: Pixabay.

Príklad 1

Vzhľadom na bod P súradníc (A, B) musíte nájsť súradnice jeho symetrického P 'týkajúceho sa pôvodu alebo súradníc (0, 0).

Prvá vec je postaviť p 'p', pre ktoré je kreslená čiara, ktorá prechádza pôvodom alebo cez bod P. Rovnica tohto riadku je y = (b/a) x.

Teraz zavolajme (a ', b') súradnice symetrického bodu p '. Bod P. Okrem toho sa musí OP vzdialenosť rovnať OP ', ktorá analyticky píše takto:

√ (a² + b²) = √ (a '² + B '² )

Nasleduje nahradenie b '= [(b/a).A '] v predchádzajúcom výraze a štvorci na oboch stranách rovnosti, aby sa eliminoval druhý koreň: (a² + b²) = [a '² + (B²/²).do '²]

Extrahovaním spoločného faktora a zjednodušením sa dosiahne “² = a². Táto rovnica má dve skutočné riešenia: a '= +a alebo a' = -a. 

Na získanie b ', znova používame b' = (b/a) a '. Ak sa nahradí pozitívny roztok A, dosiahne sa, že b '= b. A keď sa nahradí negatívny roztok, potom b '= -b. 

Môže vám slúžiť: Aké sú 7 prvkov obvodu?

Pozitívne riešenie dáva P 'rovnaký bod p, takže je vylúčené. Negatívne riešenie určite ponúka súradnice symetrického bodu:

P ': (-a, -b)

Príklad 2

Je potrebné preukázať, že segment AB a jeho symetrická centrálna A'b 'majú rovnakú dĺžku.

Počnúc súradnicami bodu A, ktoré sú (Ax, AY) a sú v bode B: (BX, by), je dĺžka AB daná:

D (ab) = √ ((bx - ax)² + (Od - ay)² )

Analogicky bude mať symetrický segment A'B 'dĺžku dĺžkou:

d (a'b ') = √ ((bx' - ax ')² + (Autor: ' - ay')² )

Súradnice symetrického bodu a 'sú ax' = -x a ay '= -ay. Podobne sú b 'bx' = -bx a '= -by. Ak sa tieto súradnice nahradia v rovnici vzdialenosti D (a'b '), máte:

D (a'b ') = √ ((-bx + ax)² + (-By + ay)²) to je rovnocenné:

 √ ((BX - AX)² + (Od - ay)²) = D (ab)

Preukázané, že oba segmenty majú rovnakú dĺžku.

Vyriešené cvičenia

- Cvičenie 1

Analyticky demonštrujte, že centrálna symetrická alebo kruh polomeru R a stredný alebo, rovnaký pôvodný obvod.

Riešenie

Rovnica polomeru R a stredného kruhu (0,0) je:

X² + a² = R² (Rovnica obvodu C)

Ak sa v každom bode P obvodu a súradnice (x, y) nachádza jeho symetrická súradnica p '), rovnica symetrického obvodu je:

X '² + a '² = R² (Symetrická obvodová rovnica C ')

Teraz hovoríme o výsledku príkladu 1, ktorý dospel k záveru, že súradnice bodu P ', symetrické k p a súradnice (a, b), sú (-a, -b). 

Ale v tomto cvičení má bod P súradnice (x, y), takže jeho symetrický P 'bude mať súradnice x' = -x e y '= -y. Toto nahradenie v symetrickej obvodovej rovnici je:

Môže vám slúžiť: Rhomboid: Charakteristiky, ako vytiahnuť obvod a oblasť

(-X)² + (-a)² = R²

Čo je rovnocenné: x²+ a² = R², záver, že centrálnou symetrickou kruhu vzhľadom na jeho centrum je samotný obvod.

- Cvičenie 2

Demonštrovať geometricky, že centrálna symetria zachováva uhly.

Riešenie

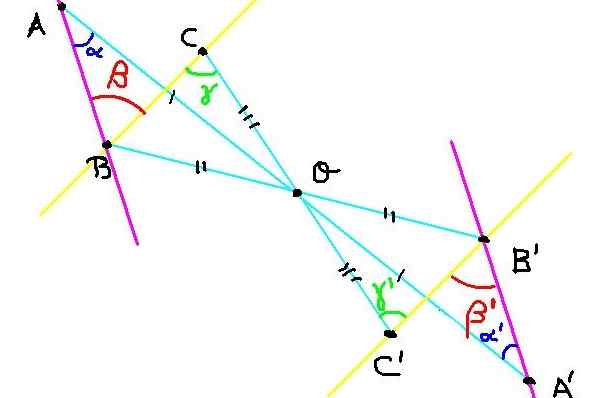Obrázok 4. Konštrukcia symetrických bodov za cvičenie 2. Zdroj: f. Zapata.

V lietadle sú tri body A, B a C. Jeho symetrické A ', B' a C 'sú postavené vzhľadom na stred symetrie alebo, ako je znázornené na obrázku 4. 

Teraz musíme preukázať, že uhol ∡abc = β má rovnaké meranie ako uhol ∡a'b'c '= β' '.

Ako C a C 'sú symetrické, potom OC = OC'. Podobne ob = ob 'y oa = oa'. Na druhej strane uhol ∡Boc = ∡b'oc 'za to, že je proti vrcholu.

Potom sú trojuholníky BOC a B'OC 'zhodné za to, že majú rovnaký uhol medzi dvoma stranami rovnaké.

Pretože BOC je zhodný s B'oc ', potom uhly  γ a γ ' Sú rovnaké. Ale tieto uhly, okrem naplnenia γ = γ ' Sú interné alternatívne medzi líniami BC a B'C, čo naznačuje, že čiara BC je rovnobežná s B'C '.

Podobne BAA je zhodným s b'oa 'toho, čo sa dodržiava α = α ' . ale  α a α ' Sú vnútorné alternatívne uhly medzi linkami BA a B'a ', z ktorých sa dospelo k záveru, že čiara BA je rovnobežná s b'a'.

Pretože uhol ∡abc = β má svoje paralelné strany s uhlom ∡a'b'c '= β' a obidve sú tiež akútne, dospelo sa k záveru:

∡ABC = ∡a'B'C '= β = β' '

Týmto spôsobom preukazuje, že centrálna symetria si zachováva mieru uhlov.

Odkazy

1. Baldor, J. Do. 1973.Geometria plochej a vesmíru. Stredoamerický kultúrny. 
2. Matematické zákony a vzorce. Meracie systémy. Zdroj: Ingemecanica.com.
3. Wentworth, G. Geometria planéty. Získané z: Gutenberg.orgán.
4. Wikipedia. Centrálna symetria. Obnovené z: je.Wikipedia.com
5. Wikipedia. Dopravník. Obnovené z: je.Wikipedia.com
6. Zapata f. Vnútorné a vonkajšie konjugované uhly. Zdroj: Lifer.com