Doplnkové uhly, ktoré a ako sa vypočítavajú, príklady, cvičenia

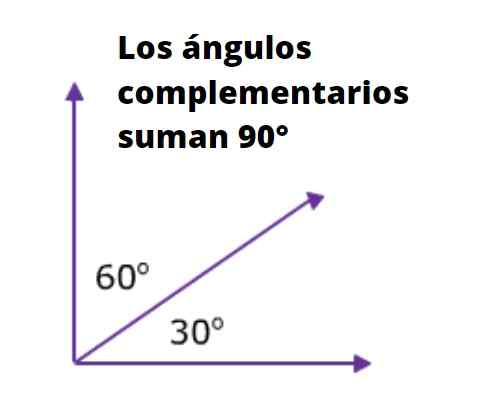
Dva alebo viac uhlov sú komplementárne uhly Ak súčet jeho opatrení zodpovedá súhrne pravého uhla. Ako je známe, miera pravého uhla v stupňoch je 90 ° a v radiánoch je π/2.

Napríklad dva uhly susediace s hypotenusom obdĺžnika trojuholníka sú navzájom doplňujúce, pretože súčet ich opatrení je 90 °. Nasledujúca hodnota je o tom veľmi ilustrovaná:

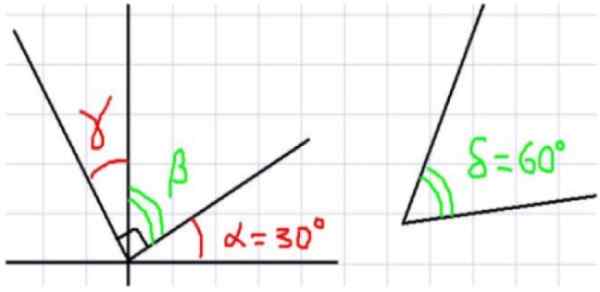postava 1. Vľavo, niekoľko uhlov s bežným vrcholom. Vpravo uhol 60 °, ktorý dopĺňa uhol a (alfa). Zdroj: f. Zapata.

Obrázok 1 zobrazuje celkom štyri uhly. α a p sú komplementárne, pretože sú susedný a jeho úplná suma pravý uhol. Podobne β je komplementárny k y, kde vyplýva, že y a a sú rovnaké.

Teraz, keďže súčet a a δ sa rovná 90 stupňom, možno povedať, že a a δ sú doplnkové. Okrem toho, keď β a δ majú rovnaký komplementárny a, možno povedať, že β a δ majú rovnaké opatrenie.

 [TOC]

Príklady doplnkových uhlov

V nasledujúcich príkladoch sa požaduje, aby našli neznáme uhly, ktoré sú uvedené s výsluchom na obrázku 2.

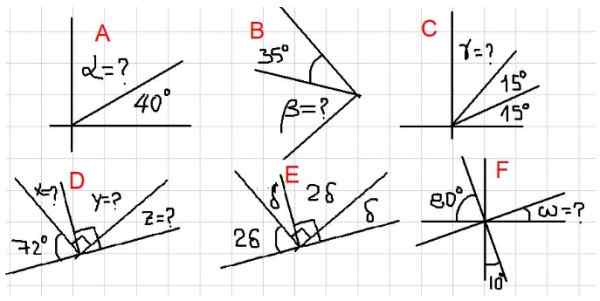Obrázok 2. Rôzne príklady doplnkových uhlov. Zdroj: f. Zapata.

- Príklady A, B a C

Nasledujúce príklady sú v poradí zložitosti.

Príklad a

Na hornej postave máme, že susedné uhly α a 40 ° sa zvyšujú do pravého uhla. To je a + 40 ° = 90 °, preto α = 90 °- 40 ° = 50 °.

Príklad B

Pretože p je doplnený uhlom 35 °, potom p = 90 ° - 35 ° = 55 °.

Môže vám slúžiť: ortoedro: vzorce, oblasť, objem, diagonálne, príklady

Príklad c

Z obrázku 2C je súčet y + 15 ° + 15 ° = 90 °. To znamená, že γ sa dopĺňa k uhlu 30 = 15 ° + 15 °. Tak to:

γ = 90 °- 30 ° = 60 °

- Príklady D, E a F

V týchto príkladoch je zapojených viac uhlov. Na nájdenie neznámych musí čitateľ uplatniť koncept doplnkového uhla toľkokrát, koľkokrát je potrebné.

Príklad d

Pretože x je doplnený 72 °, vyplýva, že x = 90 ° - 72 ° = 18 °. Navyše a je doplňujúci x, potom y = 90 ° - 18 ° = 72 °.

Konečne Z je doplňujúci a. Zo všetkých vyššie uvedených nasleduje to:

Z = 90 ° - 72 ° = 18 °

Príklad e

Uhly A a 2A sú komplementárne, preto A + 2A = 90 °.

To je 3A = 90 °, čo znamená, že δ = 90 ° / 3 = 30 °.

Príklad f

Ak zavoláme uhol medzi Ω a 10, potom sa im musí doplniť, pretože sa zistilo, že ich úplný súčet je pravým uhol. Kde z toho vyplýva, že u = 80 °. Pretože u je doplnený Ω, potom Ω = 10 °.

Cvičenia

Nižšie sú navrhnuté tri cvičenia. Vo všetkých z nich sa musí hodnota uhlov A a B nájsť v stupňoch, takže vzťahy znázornené na obrázku 3 sú splnené.

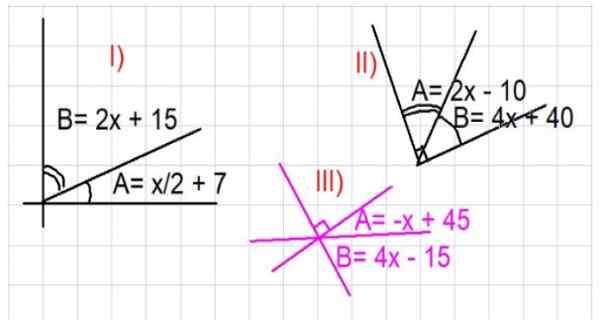Obrázok 3. Ilustrácie pre komplementárne uhly cvičenia. Zdroj: f. Zapata.

- Cvičenie 1

Stanovte hodnoty uhlov A a B časti I) na obrázku 3.

Riešenie

Z obrázku je zrejmé, že A a B sú doplnkové, preto a + b = 90 °. Expresia A a B sa nahradí ako funkcia x uvedená v časti I):

Môže vám slúžiť: Konvergenčné rádio: Definícia, príklady a cvičenia vyriešené

(x/2 + 7) + (2x + 15) = 90

Potom sú podmienky správne zoskupené a získanie jednoduchej lineárnej rovnice:

(5x/2) + 22 = 90

Odčítanie 22 v oboch členoch sú:

5x/2 = 90 -22 = 68

A nakoniec sa vymaže hodnota X:

x = 2*68/5 = 136/5

Teraz sa uhol nahradiť hodnotu x:

A = (136/5)/2 +7 = 103/5 = 20,6 °.

Zatiaľ čo uhol B je:

B = 2*136/5 + 15 = 347/5 ° = 69,4 ° .

- Cvičenie 2

Nájdite hodnoty uhlov A a B obrazu II, obrázok 3.

Riešenie

Opäť, ako A a B sú doplnkové uhly, musíte: a + b = 90 °. Nahradenie expresie A a B ako funkcie x uvedené v časti II) na obrázku 3 je:

(2x - 10) + (4x +40) = 90

Podobné výrazy sú zoskupené na získanie rovnice:

6 x + 30 = 90

Získa sa rozdelenie oboch členov medzi 6:

x + 5 = 15

Kde to vyplýva, že x = 10 °.

Preto:

A = 2*10 - 10 = 10 °

B = 4*10 + 40 = 80 °.

- Cvičenie 3

Stanovte hodnoty uhlov A a B časti III) na obrázku 3.

Riešenie

Obrázok je starostlivo analyzovaný, aby hľadal doplnkové uhly. V takom prípade musíte + b = 90 stupňov. Nahradenie výrazu A a B ako funkcie x uvedené na obrázku, máte:

(-X +45) + (4x -15) = 90

3 x + 30 = 90

Rozdelenie oboch členov 3 je nasledujúce:

x + 10 = 30

Kde to vyplýva, že x = 20 °.

To znamená, že uhol A = -20 +45 = 25 °. A pre svoju časť: B = 4*20 -15 = 65 °.

Kolmé strany uhly

Hovorí sa, že dva uhly sú kolmé strany Ak má každá strana v druhej zodpovedajúcu kolmo. Nasledujúci obrázok objasňuje koncept:

Môže vám slúžiť: zložená sukcesia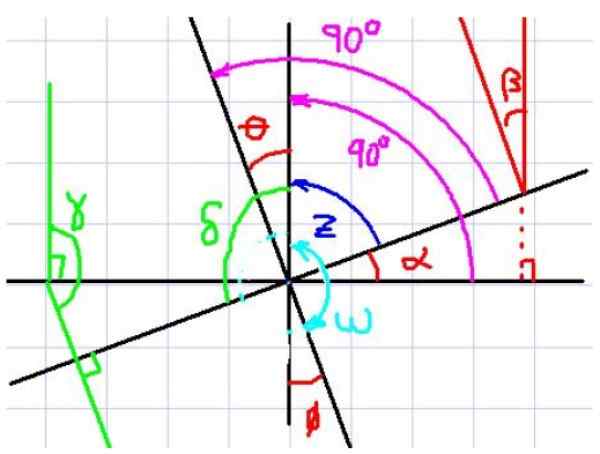Obrázok 4. Kolmé strany uhly. Zdroj: f. Zapata.

Na obrázku 4 sú pozorované napríklad uhly a a 9. Teraz si všimnite, že každý uhol má zodpovedajúci kolmo v druhom uhle.

Je tiež zrejmé, že α a 9 majú rovnaký doplnkový uhol z, Preto pozorovateľ okamžite dospel k záveru, že a a 9 majú rovnaké opatrenie. Zdá sa, že ak majú dva uhly navzájom kolmé strany, sú rovnaké, ale uvidíme iný prípad.

Teraz zvážte uhly α a Ω. Tieto dva uhly majú tiež zodpovedajúce kolmé strany, nemožno však povedať, že majú rovnakú mieru, pretože jeden je akútny a druhý je tupý.

Všimnite si, že Ω + 9 = 180 °. Okrem 9 = α. Ak nahradíte tento výraz Z v prvej rovnici, získate:

A + a = 180 °, že δ a a sú uhly vzájomne kolmých strán.

Všeobecné pravidlo uhlov kolmých strán 

Z vyššie uvedeného je možné stanoviť pravidlo, ktoré je vždy splnené, že uhly majú kolmé strany:

Ak sú dva uhly vzájomne kolmé strany, potom sú rovnaké, ak sú oba akútne alebo sú tupé. V opačnom prípade, ak je niekto akútny a druhý je tupý, potom sú doplnkové, to znamená, že pridajú 180 °.

Uplatňovanie tohto pravidla a odkaz na uhly na obrázku 4 môžeme potvrdiť:

a = β = 9 = φ

γ = δ

S doplnkovým uhlom a, β, 9 a φ.

Odkazy

1. Baldor, J. Do. 1973. Geometria plochej a vesmíru. Stredoamerický kultúrny. 
2. Matematické zákony a vzorce. Meracie systémy. Zdroj: Ingemecanica.com.
3. Wentworth, G. Geometria planéty. Získané z: Gutenberg.orgán.
4. Wikipedia. Komplementárne uhly. Obnovené z: je.Wikipedia.com
5. Wikipedia. Dopravník. Obnovené z: je.Wikipedia.com
6. Zapata f. Goniometer: História, časti, prevádzka. Zdroj: Lifer.com