Vlastnosti, príklady a cvičenia axiálnej symetrie

Ten Axiálna symetria Vyskytuje sa, keď sa body obrázku zhodujú s bodmi inej postavy pomocou priamej mediatrie nazývanej os symetrie. Nazýva sa tiež radiálna, rotačná alebo valcová symetria.

Zvyčajne sa aplikuje v geometrických číslach, ale v prírode je ľahko pozorovateľná, pretože existujú zvieratá, ako sú motýle, škorpióny, police alebo správne ľudia, ktoré prítomné axiálnej symetrie.

Na tejto fotografii horizontu mesta Toronto sa vykazuje odraz a odraz vo vode axiálnej symetrii. (Zdroj: Pixabay)

[TOC]

Ako nájsť symetrický axiálny

Na nájdenie symetrického axiálneho P 'bodu P vzhľadom na čiaru (l) sa vykonávajú nasledujúce geometrické operácie:

1.- Kolmo na čiaru (L) je sledovaný, ktorý prechádza bodom P.

2.- Odpočúvanie týchto dvoch riadkov určuje bod alebo.

3.- Meria sa dĺžka segmentu PO, potom sa táto dĺžka skopíruje na čiare (PO) od alebo v smere PA alebo určuje bod P '.

4.- Bod P.

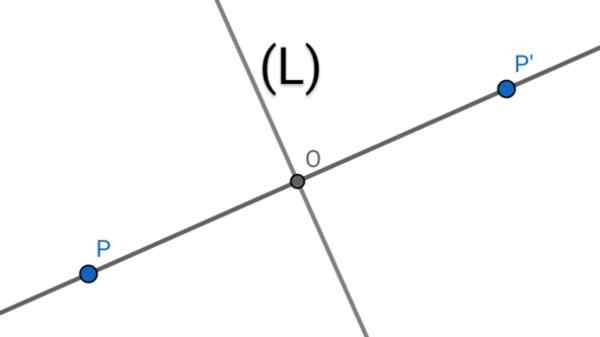postava 1. Dva body p a p 'sú axiálne symetrické k osi (l), ak je uvedená os mediatrix segmentu PP' '

Vlastnosti axiálnej symetrie

- Axiálna symetria je izometrická, to znamená vzdialenosti geometrickej postavy a jej zodpovedajúci symetrický.

- Miera uhla a jeho symetrické sú rovnaké.

- Symetrický axi bodu na osi symetrie je samotný bod.

Môže vám slúžiť: Metóda Gauss-Seidel: Vysvetlenie, aplikácie, príklady

- Symetrická čiara čiary rovnobežky so symetrickou osou je tiež stánok rovnobežná s uvedenou osou.

- Sekantná čiara k osi symetrie je symetrická.

- Symetrický obraz čiary je ďalšou čiarou, ktorá tvorí uhol s osou symetrie rovnakého merania ako pôvodná čiara.

- Symetrický obraz čiary kolmej na os symetrie je ďalšou líniou, ktorá sa prekrýva s prvou.

- Čiara a jej axiálna symetrická čiara tvoria uhol, ktorého bisektor je os symetrie.

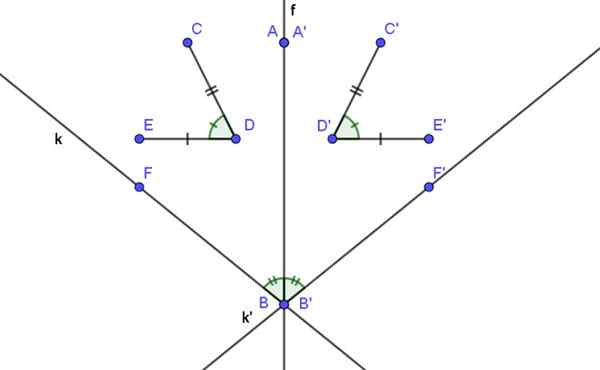Obrázok 2. Axiálna symetria zachováva vzdialenosti a uhly.

Príklady axiálnej symetrie

Príroda vykazuje množstvo príkladov axiálnej symetrie. Napríklad môžete vidieť symetriu tvárí, hmyzu, ako sú motýle, odrazy na povrchoch pokojných vôd a zrkadiel alebo listov rastlín.

Obrázok 3. Tento motýľ vykazuje takmer dokonalú axiálnu symetriu. (Zdroj: Pixabay) Obrázok 4. Tvár tohto dievčaťa má axiálnu symetriu. (Zdroj: Pixabay)

Cvičenia axiálnej symetrie

Cvičenie 1

Máte trojuholník vrcholov A, B a C, ktorého karteziánske súradnice sú a = (2, 5), b = (1, 1) a c = (3,3). Nájdite karteziánske súradnice symetrického trojuholníka vzhľadom na os y (os súradnicov).

Riešenie: Ak má bod P súradnice (x, y), potom jeho symetrický vzhľadom na os súradnicov (os y) je p '= (-x, y). Inými slovami.

Môže vám slúžiť: nekonečná súprava: Vlastnosti, príklady

V tomto prípade bude mať symetrický trojuholník vrcholov A ', B' a C 'súradnice:

A '= (-2, 5); B '= (-1, 1) a c' = (-3, 3), ako je možné skontrolovať na obrázku 6.

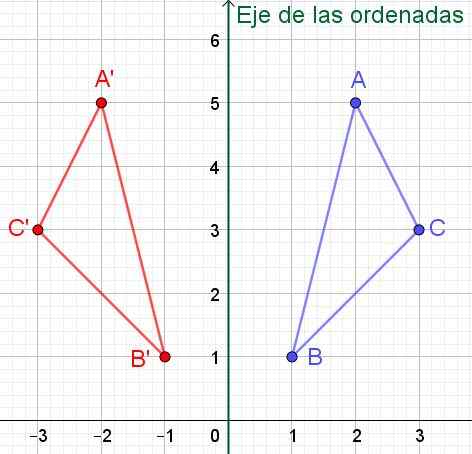Obrázok 6. Ak má bod súradnice (x, y) jeho symetrický vzhľadom na os y (os súradníc), bude mať súradnice (-x, y).

Cvičenie 2

V súvislosti s trojuholníkom ABC a jeho symetrickým a'b'c 'cvičenia 1 skontrolujte, či majú zodpovedajúce strany pôvodného trojuholníka a jeho symetrické rovnakú dĺžku.

Riešenie: Na nájdenie vzdialenosti alebo dĺžky strán používame euklidovský vzorec:

d (a, b) = √ ((bx-ax)^2 + (By-ay)^2) = √ ((1-2)^2 + (1-5)^2) = √ (-1 )^2 + (-4)^2) = √ (17) = 4,123

Ďalej sa vypočíta dĺžka symetrickej strany zodpovedajúcej „B“:

D (a ', b') = √ ((bx'-ax ')^2 +(by'-y^2) = √ ((-1 +2)^2 +(1-5)^2) = √ ((1)^2 + (-4)^2) = √ (17) = 4,123

Týmto spôsobom je dokázané, že axiálna symetria zachováva vzdialenosť medzi dvoma bodmi. Postup sa môže opakovať pre ostatné dve strany trojuholníka a jeho symetrický, aby sa skontrolovala invázia v dĺžke. Napríklad | AC | = | A'c '| = √5 = 2 236.

Cvičenie 3

Pokiaľ ide o trojuholník ABC a jeho symetrický A'b'c 'cvičenia 1, skontrolujte, či zodpovedajúce uhly pôvodného trojuholníka a ich symetrické majú rovnaké uhlové meranie.

Riešenie: Na stanovenie miery uhlov bac a b'a'c 'sa bude vypočítať najprv skalárny produkt vektorov AB s Ac a potom skalárny produkt A'b ' s A'c '.

Pamätáte si na to:

A = (2, 5), b = (1, 1) a c = (3,3)

A '= (-2, 5); B '= (-1, 1) a c' = (-3, 3).

Máš:

AB = y Ac =

podobne

A'b ' = y Ac =

Môže vám slúžiť: Lamy veta

Potom sa nájdu nasledujúce skalárne výrobky:

ABH kým = ⋅ = -1⋅1 + (-4) ⋅ (-2) = -1 + 8 = 7

Podobne

A'b'⋅a'c ' = ⋅ = 1lek (-1) + (-4) ⋅ (-2) = -1 + 8 = 7

Miera uhla BAC je:

∡bac = arccos ( ABH kým / (|AB |⋅ |AC |)) = 

Arccos (7 / (4 123,236)) = 40,6 °

Podobne miera uhla b'a'c 'je:

∡b'a'c '= arccos ( A'b'⋅a'c ' / (|A'B '|⋅ |A'c '|)) = 

Arccos (7 / (4 123,236)) = 40,6 °

Záver, že axiálna symetria zachováva mieru uhlov.

Cvičenie 4

Byť bodom súradnice (a, b). Nájdite súradnice jeho symetrického axiálneho p 'vzhľadom na čiaru y = x.

Riešenie: Zavoláme (a ', b') do súradníc symetrického bodu P 'vzhľadom na riadok y = x. Stredný bod segmentu pp 'má súradnice ((a+a')/2, (b+b ')/2) a je tiež na riadku y = x, takže je splnená nasledujúca rovnosť:

A + A '= B + B'

Na druhej strane, segment pp 'čaká na -1 na to, aby bol kolmo na čiaru y = x sklonu 1, takže je splnená nasledujúca rovnosť:

B - b '= a' -a

Vyčistenie týchto dvoch rovnosti pred „a b“ sa dospelo k záveru, že:

a '= b a čo b' = a.

To znamená, že je bod P (a, b), jeho symetrický axiálny vzhľadom na čiaru y = x je p '(b, a).

Odkazy

1. Arce m., Blázquez a ďalší. Transformácie lietadla. Získané z: EDUCUTMXLI.Súbory.Slovník.com
2. Výpočet. Axiálna symetria. Obnovené z: výpočtu.Dc
3. Superprof. Axiálna symetria. Obnovené z: Superprof.je
4. Wikipedia. Axiálna symetria. Obnovené z: je.Wikipedia.com
5. Wikipedia. Kruhový. Zdroj: In.Wikipedia.com