Typy kónických sekcií, aplikácie, príklady

Ten kužeľ Sú krivky, ktoré sa získajú zachytením lietadla s kužeľom. Existuje niekoľko spôsobov, ako to urobiť; Napríklad, ak sa rovina prechádza kolmo na axiálnu os kužeľa, získa sa obvod.

Naklonenie roviny trochu vzhľadom na axiálnu os kužeľa sa získa elipsa, krivka, ktorá je uzavretá, ale ak ju ešte viac nakloníme, získa sa parabola alebo hyperbola, ako je vidieť v animácii na obrázku 1.

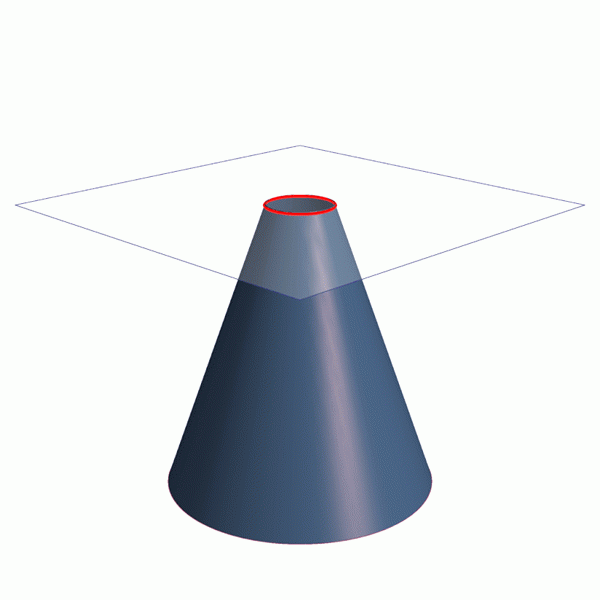Animácia, ktorá ukazuje, ako získať štyri kónické oddiely: obvod, podobenstvo a hyperbola elipsa. Zdroj: Wikimedia Commons. Riadky / CC0

KONICKÉ SEKCIE sú súčasťou prírody a sveta okolo nás. Inžinierstvo, architektúra a astronómia sú dôležitými odvetviami vedomostí, ktoré využívajú kužeľ.

[TOC]

Podmienky pre kónické sekcie

Konené úseky sú definované ako geometrické miesta, ktoré spĺňajú tieto podmienky:

Podoba

Je to geometrické miesto všetkých bodov, ktoré ležia v rovnomernej rovine k pevnému bodu zvaného zameranie F a priamka tiež pevná, nazývaná smernica.

Elipsa

Bod lietadla patrí do elipsy, ak sa nazýva súčet vzdialeností medzi týmto bodom a dvoma ďalšími fixnými bodmi, ktoré sa nazýva Foky a nachádza sa na hlavná os elipsy zostáva konštantná.

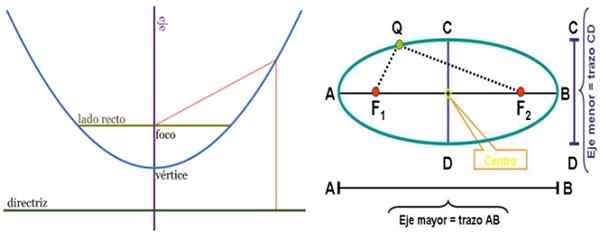Podobenstvo vľavo a elipsa napravo, s ich príslušnými prvkami. Ložiská sú body s mnohými aplikáciami. Zdroj: Wikimedia Commons.

Obvod

Je to geometrické miesto všetkých bodov, ktoré si udržiavajú rovnakú vzdialenosť k inému bodu zvaného Centro. Táto vzdialenosť je rozhlas obvodu.

Môže vám slúžiť: euklidovská vzdialenosť: koncept, vzorec, výpočet, príklad

Hyperbola

Sada bodov v rovine tak, že rozdiel medzi jeho vzdialenosťou na dva pevné body nazývaný Foky, Je to konštantné.

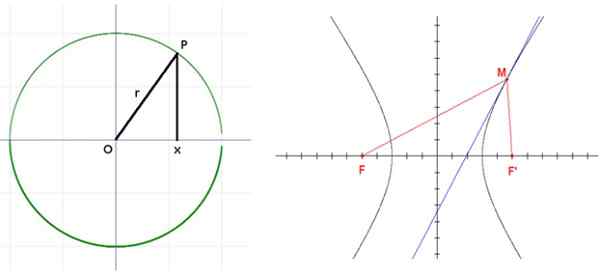Hyperbola s ložiskami f a f. Zdroj: Wikimedia Commons.

Žiadosti

Pozrime sa na niektoré z aplikácií kónických sekcií:

Podobenstvá  

-Po spustení objektu má nasledujúca trajektória podobenstvo.

-Podobenstvo majú pozoruhodné inžinierske aplikácie, napríklad v zavesených mostoch, káble sa ponáhľajú vo forme podobenstiev.

-Podarblá sú tiež dobré na výrobu reflektorov a ďalekohľadov. Je to vďaka zaujímavej vlastnosti: Pri umiestnení svietidla na bod parabolického priečneho úseku bude svetlo cestovať v paralelných lúčoch s podobenstvom.

-Ak sa svetelné lúče rovnobežné so osou symetrie priblížia k parabolickému povrchu, sústreďuje ich do zaostrenia, okolnosť, ktorá sa používa na výrobu reflektorových ďalekohľadov, ako je napríklad Teleskop Hale de Monte Palomar.

Elips

-Planéty slnečnej sústavy sa pohybujú po eliptických trajektóriách, veľmi blízko obvodu v prípade hlavných planét, zahrnula krajina. Slnko nie je v strede, ale v jednom z bodov.

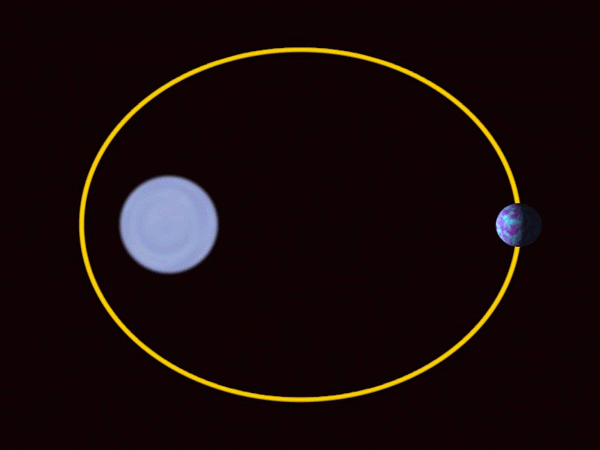Planéty slnečnej sústavy sa pohybujú v eliptických dráhach so slnkom v jednom z bodových reflektorov. Zdroj: Wikimedia Commons.

-Elipsa sa v architektúre široko používa ako dekoratívny a dizajnérsky prvok.

-Umiestnením reflektora do jedného z bodov elipsy sa svetlo odráža smerom k druhému zaostreniu. To isté sa deje so zvukom. Preto sú v Ellipse -theped Halls, ktoré hovoria potichu, ktoré sa nachádzajú v jednom zameraní.

Môže vám to slúžiť: hepagonálny hranol

-Rovnaká vlastnosť má prekvapujúcu aplikáciu v oblasti medicíny. Výpočty obličiek môžu byť zničené zvukom. Ultrazvukové vlny s veľkou intenzitou sa vytvárajú v jednej z ložisiek eliptickej vane plnej vody a pacient sa nachádza v druhom zaostrení. Zvukové vlny ovplyvňujú a odrážajú sa pri výpočte a svojou energiou ju roztrieštia v malých kúskoch, ktoré osoba potom ľahko vylúči počas močenia.

Hyperboly

-Niektoré kométy v slnečnej sústave sledujú hyperbolické trajektórie, vždy so slnkom v jednom z ohnísk.

-Zameranie hyperboly sú tiež veľmi zaujímavé na štúdium javov reflexie vĺn. Napríklad nasmerovaním lúča svetla na zameranie parabolického zrkadla sa odráža v inom zameraní, veľmi užitočnej vlastnosti na budovanie ďalekohľadov, pretože svetlo sa môže zamerať na parabolické zrkadlo a presmerovať na iné vhodnejšie miesto Podľa dizajnu.

-Chladiace veže jadrových rastlín majú siluetu v tvare hyperboly.

-Pred príchodom GPS sa pri navigácii použili hyperboly na lokalizáciu lodí. Lode prenášané na palube signálov vydávané súčasne rádiovými stanicami A a B a počítač bol zodpovedný za registráciu rozdielov v časoch príchodu signálov, aby sa premenili na rozdiely vzdialenosti vzdialeností. Týmto spôsobom sa loď nachádza v vetve hyperboly.

Postup sa opakuje s dvoma ďalšími stanicami rádiových C a D, ktoré umiestnia loď do vetvy Ďalšia hyperbola. Definitívnou polohou lode je priesečník oboch hyperboly.

Môže vám slúžiť: Rastúca funkcia: Ako ju identifikovať, príklady, cvičenia

Obvody

-Príchod kolesa zmenil priebeh histórie.

-Kruhový pohyb je veľmi častý, mnoho kusov sa točí, aby sa vytvorili rôzne účinky, od mlynov po fanúšikov.

-Aj keď trajektórie hlavných planét sú eliptické, kruhové trajektórie sú v mnohých prípadoch dobrým prístupom.

-Cirkunferencie sú častými prvkami v architektúre, dizajne, inžinierstve a konštrukcii. Zoznam kruhových alebo diskových tvarov je nekonečný: mince, CD, hodinky a ďalšie.

Príklady

Potom sú v lietadle dva kužeľ, kruh a elipsa.

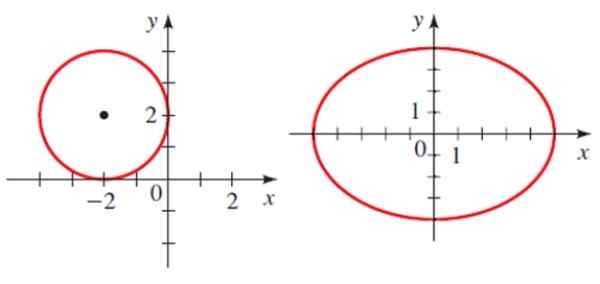Príklady kónických sekcií: kruh a elipsa. Zdroj: Stewart, J. Predbežné vyfarbenie.

Každá z nich má analytickú rovnicu:

Obvod

(X-H)² + (Y-k)² = R²

Kde H a K sú súradnice centra a R je rádio. Pre obvod zobrazený na obrázku je rovnica:

(x+2)² + (Y-2)² = 4

Elipsa

Ellipse rovnica, ktorej centrom je súradnicový bod (H, k):

[(X-H)² /² ]+ [(y-k)² /b² ] = 1

Kde a a b sú polotypily elipsy. Pre zobrazenú elipsu je centrum v bode 0,0, najväčší semifinále je rovnaký a menší semije je 4. Preto jej rovnica je:

(X² /25)+ (a² / 16) = 1

Odkazy

1. Hoffman, J. Výber matematických problémov. Zväzok 2.
2. Jiménez, r. 2008. Algebra. Sála.
3. Stewart, J. 2006. Predbežné vycvičenie: matematika na výpočet. 5. Vydanie. Učenie sa.
4. Wikipedia. Kužeľ. Obnovené z: je.Wikipedia.orgán.
5. Zill, D. 1984. Algebra a trigonometria. McGraw Hill.