Oblasť pravidelného a nepravidelného Pentagonu, ako sa užíva, cvičenia

Na výpočet oblasť Pentagonu Najprv musíme zistiť, či je to pravidelné alebo nie. Pentagón je polygón, uzavretá plochá postava piatich strán. Ak je polygón pravidelný, znamená to, že dĺžka jeho strán je rovnaká a tiež jej vnútorné uhly.

V takom prípade existuje vzorec na výpočet presnej oblasti pravidelného mnohouholníka, ktorý pozná niektoré z jeho hlavných charakteristík, ktoré odvodíme neskôr.

Dva Pentagóny

Ak polygón nie je pravidelný, to znamená, že má strany rôznych veľkostí a nerovnaké vnútorné uhly, neexistuje jediný vzorec.

Matematici však našli výpočtové stratégie, ako napríklad rozdelenie postavy na ostatných s najnižším počtom strán, ako sú trojuholníky, štvorce a obdĺžniky, ktorých rozmery sú známe alebo ľahko vypočítané.

Ďalším postupom na výpočet oblastí polygónov všeobecne, s poznaním súradníc jeho vrcholov, je metóda nazývaná metóda nazývaná Determinanty, že opíšeme neskôr.

[TOC]

Ako vypočítať plochu pravidelného Pentagonu?

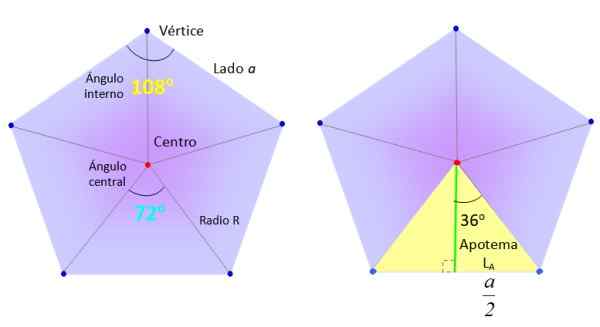
Chystáme sa brať pravidelný pentagón zo strany A a rozdelíme ho na 5 rovnakých trojuholníkov, ako je to znázornené na obrázku, čerpanie segmentov zo stredu (červenej) do vrcholov (modrá).

Potrebné prvky na nájdenie pravidelnej oblasti Pentagonu. Zdroj: f. Zapata.

Na druhej strane sú trojuholníky, ako napríklad vynikajúca žltá vpravo na hornej časti, rozdelené na dva rovnaké obdĺžniky, vďaka zelenému segmentu nazývanému apotém.

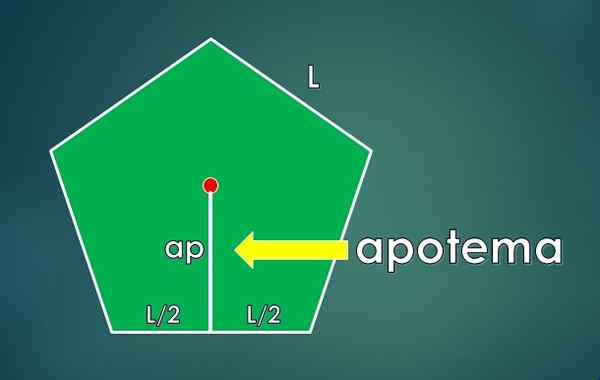
Apotheme je definovaný ako kolmo. Jeho dĺžka je l_Do.

Plocha obdĺžnika trojuholníka základne A/2 a výšky l_Do je:

[(A/2) x l_Do]

Pentagon má ako je tento 10 trojuholníkov, preto je jej oblasť:

Môže vám slúžiť: vektorové funkcie

A = 10 (a/2) x l_Do

Ale obvod P Pentagonu je presne p =10a, Preto je oblasť daná semi -produktom obvodu a dĺžkou apothémie:

A = p x l_Do /2

Pravidelná oblasť Pentagon pozná stranu a

Vyjadrujúce dĺžku apothémie l_Do V závislosti od strany A, s vedomím, že uvedený uhol je polovica centrálneho uhla, to je 36 °, čo zodpovedá:

36 ° = π/5

Elementárnou trigonometriou, dotyčnou z akútneho uhla 36 °:

Tan (π/5) = (a/2) ÷ l_Do

Teda:

L_Do=  (A/2) ÷ Tan (π/5)

Výmena v oblasti odpočítaná v predchádzajúcej časti a s vedomím, že p = 5a:

A = p x l_Do /2

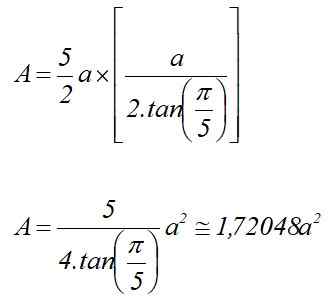
Pravidelná oblasť Pentagon pozná jeho rádio

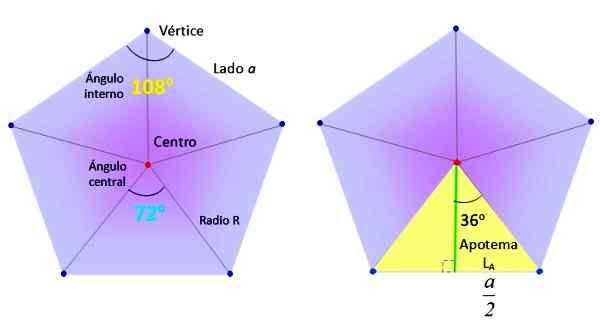
On rozhlas pravidelného mnohouholníka je segment, ktorý prechádza zo stredu do jedného zo svojich vrcholov. Zhoduje sa s polomerom ohraničeného obvodu, ako je to znázornené na nasledujúcom obrázku:

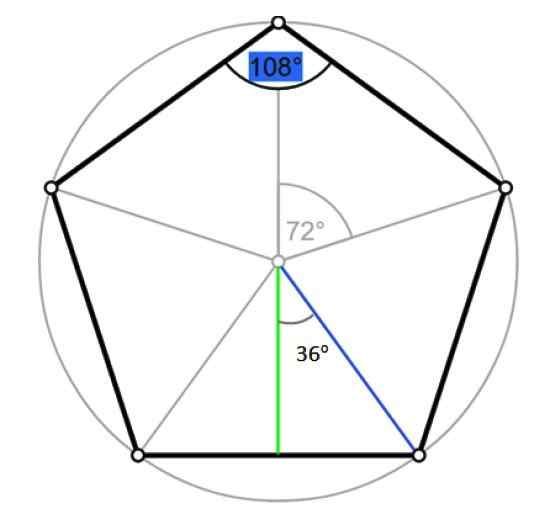Uhly a apothémia Pentagonu. Zdroj: Wikimedia Commons/F. Zapata.

Nech R je miera uvedeného rádiu, ktoré sa zhoduje s hypotenusom pravého trojuholníka vymedzeného na predchádzajúcom obrázku, modrou farbou. Podľa trigonometrie:

cos 36 ° = cos (π/5) = l_Do ÷ r

A

sin 36 ° = sin (π/5) = (a/2) ÷ r

Preto:

A = p x l_Do /2 = 5r. hriech (π/5) x r. cos (π/5) = 5r² [sin (π/5) x cos (π/5)]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]

Pomocou vzorca s dvojitým uhlom:

Sin (29) = 2 sen θ . cos θ

Musíme:

[sin (π/5) x cos (π/5)] = (1/2) sin 72 °

A tak, nahradením tejto hodnoty získame nasledujúci vzorec pre pravidelnú oblasť Pentagonu:

A = (5/2) r².Sen 72 °

Ako vypočítať oblasť nepravidelného Pentagónu?

Ako sme už povedali, pre nepravidelný polygón neexistuje jediný vzorec, ale existujú dve metódy, ktoré zvyčajne fungujú veľmi dobre, prvá sa nazýva triangulácia a druhá je metóda gauss determinantov.

Môže vám slúžiť: Existencia a jedinečnosť veta: demonštrácia, príklady a cvičenia

Triagulácia

Skladá sa z rozdelenia postavy na trojuholníky, ktorých oblasť sa ľahšie vypočítava alebo sa dá testovať aj s inými číslami, ktorých oblasť je známa, ako sú štvorce, obdĺžniky a lichobežníky.

Determinanty

Ďalším spôsobom, ako nájsť nepravidelnú oblasť Pentagonu alebo iný nepravidelný mnohouholník, je umiestnenie postavy do karteziánskeho súradnice, aby ste našli súradnice vrcholov.

Známe tieto súradnice, metóda determinantov Gauss sa používa na výpočet oblasti, ktorá je daná nasledujúcim vzorcom:

Kde a je plocha polygónu a (x_n , a_n ) sú súradnice vrcholov. Polygón N strany má 5 vrcholov, pre Pentagon by to bolo n = 5:

Tyče, ktoré sprevádzajú vzorec, sú tyče modulov alebo absolútna hodnota.

To znamená, že hoci je výsledok operácie negatívny, musíme ju vyjadriť pozitívnym znamením, a ak je už pozitívny, musí zostať s týmto znakom. Je to preto, že oblasť je vždy kladnou sumou.

Tento postup nazýva Gauss Determinants od svojho tvorcu, nemecký matematik Carl f. Gauss (1777-1855). Uvedené operácie sú ekvivalentné determinantu matice 2 x 2, napríklad prvým determinantom je:

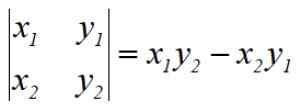
Aby sme našli oblasť Pentagonu, musíme vyriešiť 5 determinantov, pridať výsledok algebraicky, rozdeliť ju 2 a nakoniec vyjadriť oblasť vždy pozitívnym znamením.

Vyriešené cvičenia

Cvičenie 1

Nájdite pravidelnú oblasť Pentagonu, ktorej apothém má hodnotu 4 cm a ktorej vedľajšími opatreniami 5.9 cm.

Riešenie

Pretože je to pravidelný Pentagon a máme mieru strany a apothémie, používame vzorec odpočítaný predtým:

Môže vám slúžiť: Scaleno trojuholník

A = p x l_Do /2

Obvod P sa rovná 5A = 5 x 5.9 cm = 29.5 cm.

A = 29.5 cm x 4 cm / 2 = 59 cm²

Cvičenie 2

Nájdite znázornenú nepravidelnú oblasť Pentagonu. Sú známe nasledujúce rozmery:

Dc ≈ z

Ae = ab = 5

BC = 12

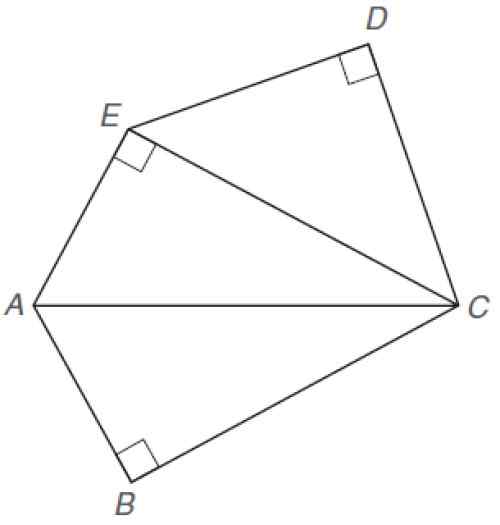Nepravidelný Pentagon. Zdroj: Alexander, D. 2013. Geometria. 5. Vydanie. Učenie sa.

Riešenie

Oblasť Pentagon je súčet oblastí trojuholníkov, ktoré sú obdĺžniky. Vo vyhlásení sa uvádza, že DC ≈, preto pri nanášaní vety Pythagoras na trojuholník EDC má:

ES² = 2 ed². Potom EC = √2.Edimatizovať.

AEC a ABC trojuholníky majú spoločnú hypotenus, ktorá je segmentom AC, preto:

EA² + ES² = Ab² + Bc²

Ako EA a AB merajú rovnako, získa sa:

EC = BC = √2.Edimatizovať

Pretože BC = 12, potom ed = 12 / √2 = 8.485.

S týmito hodnotami vypočítame plochu každého trojuholníka a pridáme ich na konci.

Oblasť trojuholníka EDC 

Ed x dc /2 = 8.485² / 2 = 36

AEC trojuholníka 

EA x EC / 2 = EA x √2.ED / 2 = 5 x √2. 8.485/2 = 30

Oblasť trojuholníka ABC 

AB X BC / 2

Potom požadovaná oblasť je:

5 x 12/2 = 30

Je to rovnaké ako v prípade trojuholníka AEC, pretože obe majú rovnaké opatrenia.

Nepravidelná oblasť Pentagonu

Nakoniec požadovaná oblasť je súčet oblastí troch trojuholníkov:

A = 36 + 30 + 30 jednotiek = 96 jednotiek.

Odkazy

1. Alexander, D. 2013. Geometria. 5. Vydanie. Učenie sa.
2. Matematika otvorená referencia. Polygón. Získané z: Mathpenref.com.
3. Vesmír. Oblasť nepravidelného Pentagonu. Získané z: Universoformulas.com.
4. Vesmír. Oblasť pravidelného Pentagonu. Získané z: Universoformulas.com.
5. Wikipedia. Priechod. Obnovené z: je.Wikipedia.com.