Druhý koreň 3 (ľahké riešenie a vysvetlenie)

Druhý koreň 3 je 1,73205080756887.

Dá sa vyjadriť:

√3 = 1,73205080756887

Vedieť, čo je 3 druhý koreň, Je dôležité poznať definíciu odmocniny čísla. Vzhľadom na kladné číslo „A“ je druhý druhá koreň „A“ označená √A kladné číslo „B“, takže keď sa „B“ vynásobí, výsledkom je „a“.

Matematická definícia hovorí: √a = b áno, a iba v prípade, b² = b*b = a. Preto, aby sme vedeli, aký je druhá odmocnina 3, tj hodnota √3, číslo „b“, je potrebné zistiť, že b² = b*b = √3.

Okrem toho je √3 iracionálne číslo, ktoré pozostáva z nekonečného neperiodického množstva desatinných miest. Z tohto dôvodu je ťažké vypočítať odmocninu 3 ručne.

3 druhý koreň

Ak sa použije kalkulačka, je zrejmé, že druhá druhá koreň 3 je 1,73205080756887…

Teraz by ste sa mohli manuálne pokúsiť priblížiť toto číslo takto:

-1*1 = 1 a 2*2 = 4, hovorí sa, že druhá druhá koreň 3 je číslo medzi 1 a 2.

-1,7*1,7 = 2,89 a 1,8*1,8 = 3,24, preto je prvý desatinný obrázok 7.

-1,73*1,73 = 2,99 a 1,74*1,74 = 3,02, takže druhý desatinný obrázok je 3.

-1 732*1,732 = 2,99 a 1 733*1,733 = 3 003, preto tretí desatinný obrázok je 2.

A tak ďalej, môžete pokračovať. Toto je manuálny spôsob výpočtu druhej odmocniny 3.

Existujú aj ďalšie oveľa pokročilejšie techniky, ako napríklad Newton-Raphsonova metóda, čo je numerická metóda na výpočet aproximácií.

Kde nájdeme číslo √3?

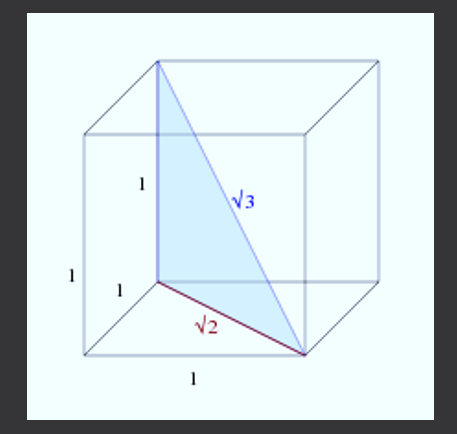
Kvôli zložitému počtu by sa dalo myslieť, že sa neobjavuje v každodenných objektoch, ale je to nepravdivé. Ak máte kocku (štvorcový box), takže dĺžka jej strán je 1, potom kocka diagonály budú mať mieru √3.

Aby som to overil, používa sa veta Pythagoras, ktorá hovorí: Daj.

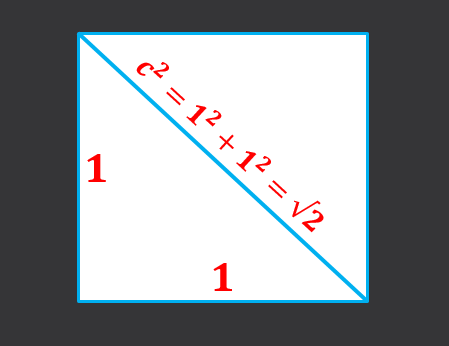
Mať stranu strany 1, musíte diagonálnu štvorcovú základňu rovná súčtu štvorcov kategórií, tj C² = 1²+1² = 2, preto diagonála základnej miery √2.

Teraz na výpočet diagonálu kocky môžete vidieť nasledujúci obrázok.

Nový obdĺžnikový trojuholník má nohy dĺžiek 1 a √2, preto pri použití vety Pythagoras na výpočet dĺžky jej diagonálu sa získa: C² = 1²+(√2) ² = 1+2 = 3, povedzme , C = √3.

Dĺžka diagonálu bočného vedra 1 sa teda rovná √3.

√3 Iracionálne číslo

Na začiatku sa hovorilo, že √3 je iracionálne číslo. Aby som to overil, predpokladá sa to absurditou, ktorá je racionálnym číslom, ktoré existujú dve čísla „A“ a „B“, relatívnych bratrancov, ako napríklad A/B = √3.

Keď sa získa posledná rovnosť a jasná „a²“, získa sa nasledujúca rovnica: a² = 3*b². To hovorí, že „A²“ je násobok 3, ktorý dospel k záveru, že „A“ je násobok 3.

Byť „násobkom 3, je tu celé číslo“ K “také, že a = 3*. Preto sa nahradí v druhej rovnici, ktorá sa získa: (3*k) ² = 9*k² = 3*b², čo je rovnaké ako b² = 3*k².

Rovnako ako predtým, táto posledná rovnosť vedie k záveru, že „B“ je násobok 3.

Záverom je, že „A“ a „B“ sú násobky 3, čo je protirečenie, pretože spočiatku sa predpokladalo, že to boli relatívni bratranci.

Preto je √3 iracionálne číslo.