Čo sú interné alternatívne uhly? (S cvičeniami)

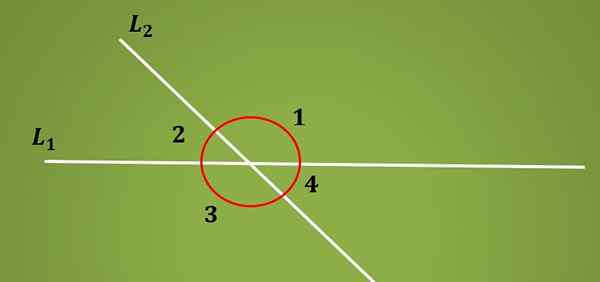
Ten interné alternatívne uhly Sú to uhly tvorené priesečníkom dvoch paralelných čiar a priečnej čiary. Keď je čiara L1 odrezaná pomocou priečneho riadku L2 4 uhly sa vytvoria uhly.

Dva páry uhlov, ktoré zostávajú na rovnakej strane línie L1, sa nazývajú doplnkové uhly, pretože jeho súčet sa rovná 180 °. Na dolnom obrázku sú uhly 1 a 2 doplnkové, ako aj uhly 3 a 4.

Aby sme hovorili o vnútorných alternatívnych uhloch, je potrebné mať dve paralelné čiary a priečnu čiaru; Ako je vidieť predtým, vytvorí sa osem uhlov.

Ak sú dve paralelné čiary L1 a L2 rezané priečnou čiarou, vytvorí sa osem uhlov, ako je znázornené na nasledujúcom obrázku.

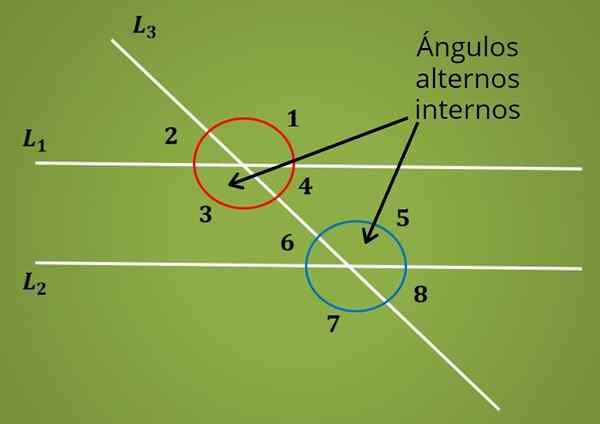
Na vynikajúcom obrázku sú páry uhlov 1 a 2, 3 a 4, 5 a 6, 7 a 8 doplnkové uhly. 

Teraz sú vnútorné alternatívne uhly medzi dvoma rovnobežnými čiarami L1 a L2, ale sú umiestnené na opačných stranách priečnej čiary L2. To je Uhly 3 a 5 sú vnútorné alternatívne. Podobne uhly 4 a 6 sú vnútorné alternatívne uhly.

Protichodné uhly podľa vrcholu

Ak chcete poznať užitočnosť, ktoré majú interné alternatívne uhly, je potrebné najprv vedieť, že ak sú dva uhly proti vrcholu, potom tieto dva uhly zmerajú rovnaké.

Napríklad uhly 1 a 3 merajú rovnaké ako v súlade s vrcholom. Podľa rovnakého zdôvodnenia je možné dospieť k záveru, že uhly 2 a 4, 5 a 7, 6 a 8 merajú to isté.

Uhly vytvorené medzi secant a dvoma paralelmi

Ak sú dve paralelné čiary rezané suchou alebo priečnou čiarou ako na predchádzajúcom obrázku, je pravda, že uhly 1 a 5, 2 a 6, 3 a 7, 4 a 8 merajú rovnaké.

Interné alternatívne uhly

Pomocou definície uhlov umiestnených vrcholom a vlastnosti uhlov vytvorených medzi sekundárnymi a dvoma rovnobežnými čiarami je možné dospieť k záveru, že vnútorné alternatívne uhly majú rovnaké opatrenie.

Vyriešené cvičenia

- Prvé cvičenie

Vypočítajte mieru uhla 6 z nasledujúceho obrázka, s vedomím, že uhol 1 meria 125 °.

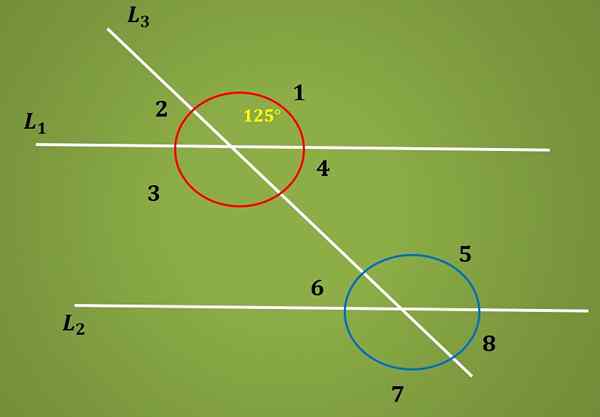
Riešenie

Pretože uhly 1 a 5 sú proti vrcholu opačné, máte tento uhol 3 meria 125 °. Teraz, pretože uhly 3 a 5 sú vnútorné alternatívne, máte tento uhol 5 tiež meria 125 °.

Nakoniec, pretože uhly 5 a 6 sú doplňujúce, miera uhla 6 sa vyžaduje rovná 180 ° - 125 ° = 55 °.

- Druhé cvičenie

Vypočítajte uhol 3 s vedomím, že uhol 6 meria 35 °.

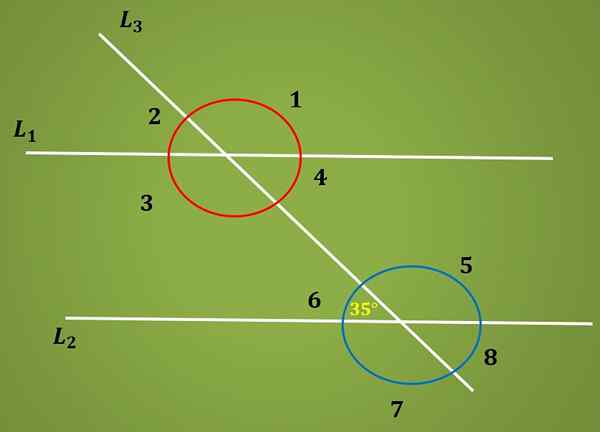
Riešenie

Je známe, že uhol 6 meria 35 ° a je tiež známe, že uhly 6 a 4 sú vnútorné alternatívne, preto merajú rovnaké. To znamená, že uhol 4 meria 35 °.

Na druhej strane, pomocou skutočnosti, že uhly 4 a 3 sú doplnkové, miera uhla 3 sa rovná 180 ° - 35 ° = 145 °.

Pozorovanie

Je potrebné, aby čiary boli rovnobežné, aby mohli splniť zodpovedajúce vlastnosti.

Cvičenia sa môžu vyriešiť rýchlejšie, ale tento článok chcel použiť vlastnosť interných alternatívnych uhlov.

Odkazy

1. Buchnúť. (2007). Uhol z geometrie matematické zošit. Učenie sa NewPath.
2. Clemens, s. R., O'Dafer, P. G., & Cooney, T. J. (1998). Geometria. Pearson Vzdelanie.
3. Lang, s., & Murrow, G. (1988). Geometria: stredoškolský kurz. Springer Science & Business Media.
4. Lira, a., Jaime, P., Chavez, m., Gallegos, m., & Rodríguez, C. (2006). Geometria a trigonometria. Utajené vydania.
5. Moyano, a. R., Saro, a. R., & Ruiz, R. M. (2007). Algebra a kvadratická geometria. Netbiblo.
6. Sullivan, m. (1997). Trigonometria a analytická geometria. Pearson Vzdelanie.
7. Wingard-Edenelson, R. (2012). Geometria. Enslow Publishers, Inc.