Aký je magnetický moment?

On Magnetický moment Je to vektor, ktorý sa týka prúdu, ktorý prechádza trochu alebo zatvorenou slučkou s rovnakou plochou. Jeho modul sa rovná produktu intenzity prúdu v oblasti a jeho smer a smer sú dané pravidlom pravej ruky, ako je znázornené na obrázku 1.

Táto definícia je platná bez ohľadu na to. Pokiaľ ide o jednotu magnetického momentu, v medzinárodnom systéme jednotiek, ak je ampér × m².

postava 1. Magnetický momentový vektor ľubovoľnej súčasnej väzby je kolmá na svoju rovinu a smer je určený pravým pravidlom. Zdroj: Wikimedia Commons.

Z matematického hľadiska označovanie vektorového magnetického momentu s gréckymi textami μ (Výrazne, pretože je to vektor, a tak sa odlišuje od jeho veľkosti), je vyjadrený ako:

μ = Ia n

Kde som intenzita prúdu, A je oblasť, ktorá uzatvára slučku a n Je to jednotkový vektor (modulu rovnajúceho sa 1), ktorý ukazuje v smere kolmom na rovinu spary a ktorého význam je daný pravidlom pravého palca (pozri obrázok 1).

Toto pravidlo je veľmi jednoduché: stočenie štyroch prstov pravej ruky, aby nasledovali prúd, palec označuje smer a smer n a preto magnetický moment.

Predchádzajúca rovnica je platná pre slučku. Ak sú Nougas ako v cievke, magnetický moment sa vynásobí n:

μ = nIa n

[TOC]

Magnetický moment a magnetické pole

Je ľahké nájsť výrazy pre magnetický moment zákrut s bežnými geometrickými tvarmi:

-Štvorcová strana strany ℓ: μ = Iℓ² n

-Strany obdĺžniková špirála do a b: μ = Iab n

-Radio R. Radio Spira: μ = Iπr² n

Môže vám slúžiť: atómové číslo

Dipoloho magnetické pole

Magnetické pole produkované prúdovou slučkou alebo spázou sa podobá na tyčí magnetu a tiež na zem Zeme.

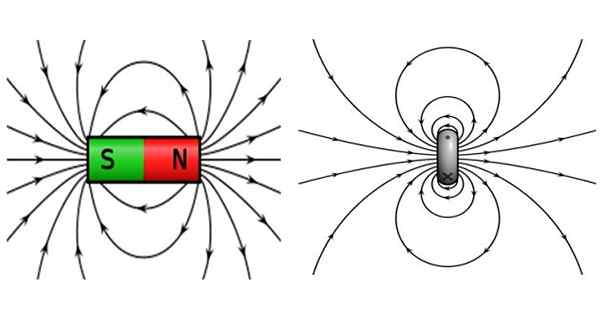Obrázok 2. Vľavo magnetické pole tyčového magnetu a doprava, ktorá vytvára kruhovú špirálu, ktorá transportuje prúd. Zdroj: Wikimedia Commons.

Magnety stĺpcov sa vyznačujú tým, že majú severný pól a južný pól, kde sú priťahované protiľahlé póly, a rovnaké póly odpudzujú. Poľné čiary sú zatvorené, opúšťajú severný pól a dostanú sa na južný pól.

Teraz sú magnetické póly neoddeliteľné, čo znamená, že ak je stĺpcový magnet rozdelený na dva menšie magnety, naďalej majú svoje vlastné severné a južné póly. Nie je možné mať izolované magnetické póly, a preto sa nazýva stĺpcový magnet Magnetický dipolo.

Magnetické pole polomeru r špirálovej r, ktorá transportuje prúd I, sa vypočítava podľa zákona Biot-Savart zákon. Pokiaľ ide o body patriace k jeho osi symetrie (v tomto prípade os x) je pole dané:

Kde μ_ani Je to priepustnosť vákua. Vráťte pole na body od spary, pre ktorú je splnené, že x >> r sa pole blíži:

Vzťah medzi magnetickým poľom a magnetickým momentom dipola

Vrátane magnetického momentu v predchádzajúcom výraze je:

Týmto spôsobom je intenzita magnetického poľa úmerná magnetickému momentu. Všimnite si, že intenzita poľa klesá s kockou vzdialenosti.

Tento prístup sa vzťahuje na akúkoľvek slučku, pokiaľ X byť v porovnaní s jeho rozmermi veľký.

A keďže čiary tohto poľa sa podobajú líniám tyčového magnetu, rovnica je dobrým modelom pre toto magnetické pole a modely iných systémov, ktorých čiary sú podobné, napríklad: napríklad:

Môže vám slúžiť: Absorbancia: Čo je, príklady a cvičenia vyriešené

-Častice načítané v pohybe ako elektrón.

-Atóm.

-Zem a iné planéty a satelity slnečnej sústavy.

-Hviezda.

Vplyv vonkajšieho poľa na slučku

Veľmi dôležitou charakteristikou magnetického momentu je jeho prepojenie s krútiacim momentom, že slučka zážitok v prítomnosti vonkajšieho magnetického poľa.

Elektrický motor obsahuje cievky, cez ktoré prechádza prúd zmeny smeru a že vďaka externému poľa zažije efekt otočenia. Tento otáčok spôsobí, že sa pohyb pohne a elektrická energia sa počas procesu stáva mechanickou energiou.

Krútiaci moment na obdĺžnikovej slučke

Predpokladajme, že na uľahčenie výpočtov je obdĺžnikové strany do a b, ktorého normálny vektor n, Odchádzajúca obrazovka, spočiatku je kolmá na jednotné magnetické pole B, ako na obrázku 3. Strany slučkových skúseností sily, ktoré poskytuje:

F = IL X B

Kde L Je to vektor veľkosti rovnajúci sa dĺžke segmentu a nasmerovaný podľa prúdu a je intenzitou toho istého a B Je to pole. Sila je kolmá na obidve L Rovnako ako pole, ale nie všetky strany zažívajú silu.

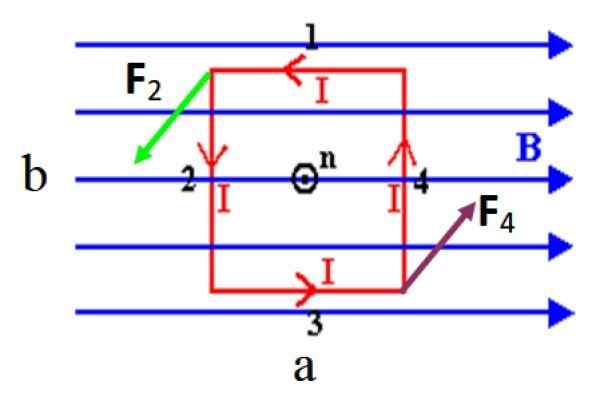Obrázok 3. Obdĺžniková špirála, ktorá transportuje prúd I v anti -horskom zmysle, zažíva krútiaci moment v prítomnosti rovnomerného rovnomerného magnetického poľa. Zdroj: f. Zapata.

Na obrázku nie je na krátkych stranách 1 a 3 žiadna pevnosť na paralelné s poľom, nezabudnite, že prierez medzi paralelnými vektormi je neplatný. Dlhé strany 2 a 4, ktoré sú kolmé na B, zažívajú označované sily ako F₂ a F₄.

Tieto sily tvoria pár: Majú rovnakú veľkosť a smer, ale opačné zmysly, preto sa nedokážu presunúť do slučky v strede poľa. Ale môžu ho prinútiť otáčať sa, pretože krútiaci moment  τ Že každá sila vyvíja, vzhľadom na vertikálnu os, ktorá prechádza stredom slučky, má rovnaký smer a význam.

Môže vám slúžiť: súdržná sila

Podľa definície krútiaceho momentu, kde r Je to polohový vektor:

τ = r X F

Tak:

τ₂ = τ₄=(A/2) f (+J )

Jednotlivé krútiace momenty nie sú zrušené, pretože majú rovnaký smer a význam, potom sú pridané:

τ_slepo = τ₂ + τ₄ = f (+J )

A keďže je veľkosť sily f = IBB, výsledkom je:

τ_slepo = I šložený na+J )

Produkt A zajtra je oblasť A Spipas, takže IAB je veľkosť magnetického momentu μ. Preto τ_slepo = μ⋅b (+J )

Je zrejmé, že vo všeobecnosti sa krútiaci moment zhoduje s vektorovým produktom medzi vektormi μ a B:

τ_slepo = μ X B

A hoci tento výraz bol odvodený z obdĺžnikovej slučky, je platný pre ploché opory svojvoľne.

Účinok poľa na slučku je krútiaci moment, ktorý má tendenciu zarovnať magnetický moment s poľom.

Potenciálna energia magnetického dipólu

Aby sa otočil špirála alebo dipól uprostred poľa, musí sa vykonávať práca proti magnetickej sile, ktorá mení potenciálnu energiu dipola. Variácia energie Au, keď sa špirála otáča z uhla 9_ani V uhle 9 je daný integrálom:

Ak je referenčná úroveň vybraná ako 9_ani = π/2:

ΔU = -μb cos θ

Ktorý sa dá zase vyjadriť ako skalárny produkt medzi vektormi B a μ:

ΔU = - ·B

Minimálna potenciálna energia v dipóle dochádza, keď cos θ = 1, čo znamená, že to znamená μ a B Sú rovnobežné, energia je maximálna, ak sú opačné (9 = π) a je nulová, keď sú kolmé (9 = π/2).

Odkazy

1. Figueroa, D. 2005. Séria: Fyzika pre vedu a inžinierstvo. Zväzok 5. Elektromagnetizmus. Editoval Douglas Figueroa (USB).
2. Resnick, r. 1999. Fyzický. Zvuk. 2. 3. vydanie. v španielčine. Kontinentálna redakčná spoločnosť s.Do. c.Vložka.
3. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 2. Pearson.
4. Serway, r., Jewett, J. (2008). Fyzika pre vedu a inžinierstvo. Zväzok 2. 7. Edimatizovať. Učenie sa.
5. Tipler, P. (2006) Fyzika pre vedu a techniku. 5. vydanie. Zväzok 2. Redaktor sa vrátil.