Aký je rezací, tuhý alebo šmykový modul? (Vyriešené cvičenia)

On Prerezaný modul Opíšte reakciu materiálu na uplatňovanie šmykového úsilia, ktoré ho deformuje. Ďalšími častými používanými nomináciami pre rezací modul sú strihy, strihy, priečna elasticita alebo tangenciálny modul elasticity.

Ak je úsilie malé, deformácie sú im podľa Hookeho zákona úmerné. Preto:

Cut Module = úsilie o rezanie/deformáciu

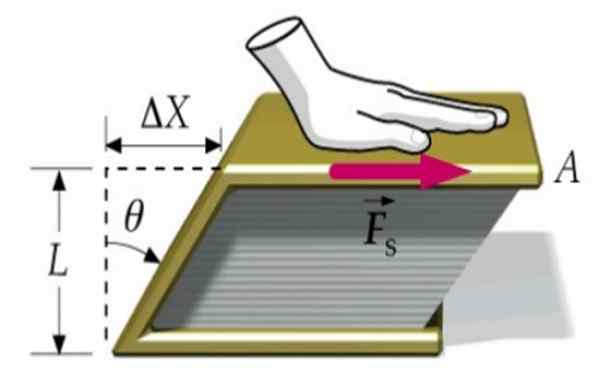
postava 1. Kniha je zdeformovaná vďaka tangenciálnej sile FS. Zdroj: f. Zapata.

Predpokladajme, že na veko knihy sa aplikuje sila, ktorá je druhá pripevnená na povrch stola. Týmto spôsobom sa kniha ako celok nepohybuje, ale deformuje sa, keď sa horné veko pohybuje vzhľadom na spodnú časť v množstve Δx.

Kniha prechádza z obdĺžnikovej priečnej časti do sekcie vo forme rovnobežníka, ako vidíme v vynikajúcom obrázku.

Byť:

τ = f/a

Úsilie alebo rezanie napätia, bytie F veľkosť aplikovanej sily a Do Oblasť, v ktorej koná.

Spôsobené deformácie je dané kvocientom:

δ = δx / l

Preto rezací modul, ktorý označíme ako G, je:

Týmto spôsobom je rezací modul zodpovedný za meranie odporu vnútorných rovín objektu, ktoré sú rovnobežné s aplikovaným úsilím.

A keďže Δx / l chýbajú rozmery, jednotky G sú rovnaké ako jednotky rezného úsilia, čo je dôvod medzi silou a oblasťou.

V medzinárodnom systéme jednotiek sú tieto jednotky Newton/Square Metro alebo Pascal, skrátene PA. A v anglo -asaxonských jednotkách je to skrátene psi.

[TOC]

Môže vám slúžiť: Rovnomerný priamy pohyb: Charakteristiky, vzorce, cvičenia

Cut Modul pre rôzne materiály

Pri pôsobení rezných síl, ako sú opísané sily, ponúkajú objekty odpor podobný odporu knihy, v ktorej sa vnútorné vrstvy posúvajú. Tento typ deformácie sa môže vyskytnúť iba v pevných telách, ktoré majú dostatočnú rigiditu na to, aby boli deformované.

Na druhej strane tekutiny neponúkajú tento druh odporu, ale môžu zažiť deformácie objemu.

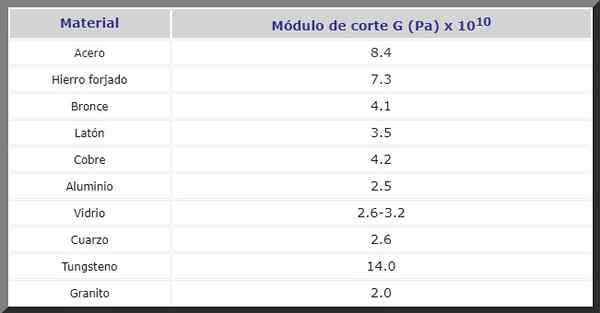
Obrázok 2. Skrutky v štruktúrach sú predmetom úsilia o rezanie. Zdroj: pixnio.

Ďalej máte modul G -Nakant v P pre rôzne materiály, ktoré sa často používajú vo výstavbe a pri výrobe strojov a náhradných dielov všetkých druhov:

Experimentálne meranie rezacieho modulu

Ak chcete nájsť hodnotu rezného modulu, musíte otestovať vzorky každého materiálu a preskúmať svoju odpoveď na použitie úsilia o rezanie.

Vzorka je tyč vyrobená z materiálu, s rádiom R a dĺžka L Známy, ktorý je pripevnený na jednom konci, zatiaľ čo druhý sa pripája k osi voľnej kladky.

Kladka má zviazané lano, na ktorého voľnom konci je váha zavesená, ktorá vyvíja silu F Na tyči cez lano. A táto sila zase vytvára okamih M V tyče, ktorá potom otočí malý uhol 9.

Na nasledujúcom obrázku je možné vidieť schému montáže:

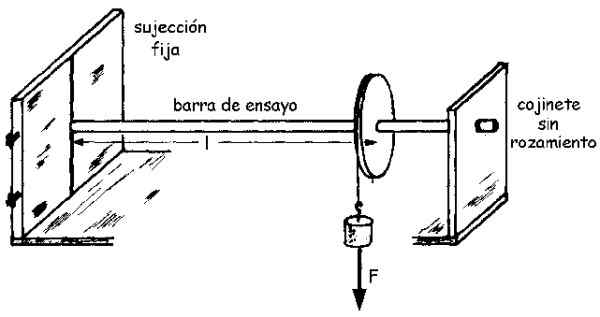Obrázok 3.- Experimentálna zostava na stanovenie šmykového modulu alebo reznej skúšobnej tyče. Zdroj: University of Valladolid.

Veľkosť okamihu M, ktoré označujeme ako M (bez tučného tuku) súvisí s uhlom otočeným 9 cez modul rezu g podľa nasledujúcej rovnice (je odvodený jednoduchým integrálom):

Pretože veľkosť tohto momentu sa rovná produktu modulu sily F polomerom kladky r_p:

Môže vám slúžiť: Torricelli Experiment: Opatrenia atmosférického tlaku, dôležitosť

M = f.R_p

A sila je váha, ktorá visí W, tak:

M = w.R_p

Nahradenie v rovnici rozsahu okamihu:

Máte vzťah medzi hmotnosťou a uhlom:

Ako nájsť g?

Tento vzťah medzi premennými W a θ Je lineárny, takže sa merajú rôzne uhly, ktoré sa vyrábajú visí rôznymi hmotnosťami.

Páry hmotnosti a uhla sú grafy na milimetrovom papieri, najlepšia čiara, ktorá prechádza experimentálnymi bodmi, je upravená a vypočíta sa sklon m uvedená čiara.

 Odtiaľ to nasleduje:

Cvičenia s roztokom

- Cvičenie 1

2 tyč.5 metrov dlhé a rádio 4.5 mm je fixovaný na jednom konci. Druhý sa pripája k 75 cm rádiovej kladke, ktorá má hmotnosť 1 1.3 kg. Zmenený uhol je 9.5.

S týmito údajmi sa požaduje vypočítať rezací modul g tyče.

Riešenie

Z rovnice:

Gasses G:

A hodnoty uvedené vo vyhlásení sú nahradené, pričom sú opatrné, aby vyjadrili všetky údaje v medzinárodnom systéme jednotiek, ak:

R = 4.5 mm = 4.5 x 10 ^-3 m

R_p = 75 cm = 0.075

Prechod z kilogramov (v skutočnosti sú to kilogramy - sila) do Newtonu vynásobí 9.8:

W = 1.3 kg-force = 1.3 x 9.8 n = 12.74 n

A nakoniec, stupne musia byť na radiánoch:

9.5. = 9.5 x2π /360 radiánov = 0.1658 Radiany.

S tým všetkým máte:

= 2.237 x 10¹⁰ Pav

- Cvičenie 2

Gélová kocka je 30 cm strana. Jedna z jeho tvárí je pevná, ale zároveň sa na opačnú tvár aplikuje paralelná sila 1 N, ktorá vďaka tomuto pohybu 1 cm (pozri príklad knihy na obrázku 1).

Môže vám slúžiť: magnetizácia: orbitálny a rotátny magnetický moment, príklady

Vyžaduje sa, aby sa s týmito údajmi vypočítal:

a) veľkosť šmykového napätia

b) jednotná deformácia δ

c) Hodnota rezného modulu

Roztok

Veľkosť šmykového napätia je:

τ = f/a

S:

A = strana² = (30 x 10^-2 cm)² = 0.09 m²

Preto:

τ = 1 n / 0.09 m² = 11.1 pa

Riešenie B

Unitárna deformácia nie je iná ako hodnota δ, daná:

δ = δx / l

Posun tváre vystavenej sile je 1 cm, potom:

δ = 1/30 = 0.0333

Riešenie c

Rezací modul a kvocient medzi úsilím o rezanie a deformáciou jednotky:

G = úsilie o rezanie/deformáciu

Preto:

G = 11.1 pa /0.033 = 336.4 PA

Odkazy

1. Pivo, f. 2010. Mechanika materiálov. McGraw Hill. 5. Vydanie.
2. Franco Garcia,. Tuhý. Počuť meranie modulu. Zdroj: SC.Ehu.je.
3. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6. Ed Prentice Hall.
4. Resnick, r. (1999). Fyzický. Zvuk. 1. 3. vydanie. v španielčine. Kontinentálna redakčná spoločnosť s.Do. c.Vložka.
5. University of Valladolid. Katedra fyziky kondenzovaných látok. Výber problémov. Obnovené z: www4.hitva.je.