Rybárske vlastnosti

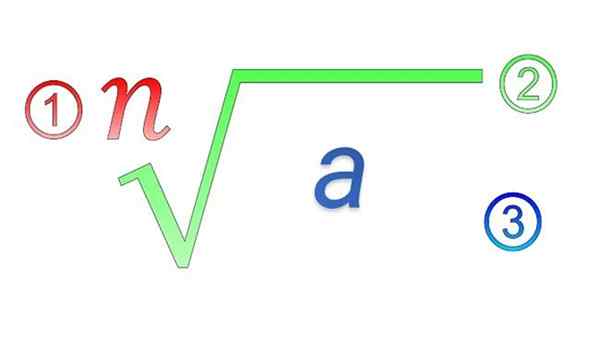
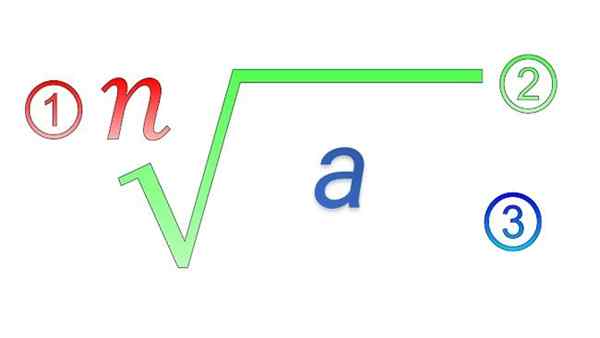Radikálne prvky: 1) index; 2) radikálny symbol; 3) subradické množstvo

Aké sú vlastnosti radikálov?

Ten rybárske vlastnosti Sú to operácie, ktoré umožňujú riešenie zložitých problémov radikálov a síl. Radical je spôsob, ako matematicky symbolizovať N-Eme sumy „a“. Táto koreň je ďalšia suma nazývaná „B“, takže jeho názov je presne „A“, takže je platné písať nasledujúce:

Hodnota „N“ je prirodzené číslo, ktoré je známe ako koreňový index, „A“ je Radikujúci alebo subradické množstvo a „b“ je n-eme koreňov „A“. „A“ aj „B“ patria do súboru skutočných čísel.

Ak index nie je napísaný v radikáli, okamžite sa chápe, že jeho hodnota sa rovná 2 a znie „druhý koreň A“.

Pretože "n" patrí do súboru prírodných čísel, môže to byť pár alebo nepárne číslo. Potom sa rozlišujú nasledujúce prípady:

Pre "n" par

• Ak a> 0 alebo rovnajú sa 0, koreň N-alka „a“ je kladný alebo 0 a nazýva sa to hlavný koreň.
• Kedy < 0, no existe raíz n-ésima en el conjunto de los números reales, pero sí en los números complejos.

Pre „n“ nepárne

• Áno a> 0, n-eme koreňa „A“ je pozitívny.
• Kedy< 0, la raíz n-ésima de “a” es negativa.

Niektoré príklady sú nasledujúce:

Natáčanie

Je možné napísať názov sumy sumy ako silu s zlomkom exponentom, to znamená racionálne číslo.

V tomto prípade sa koreňový index stáva menovateľom, zatiaľ čo exponent subradickej sumy sa stáva čitateľom:

Môže vám slúžiť: Homografická funkcia: Ako graf, vyriešené cvičenia

Výraz, ktorý je platný, pokiaľ N ≠ 0, pretože nie sú prijaté žiadne frakcie s menovateľom.

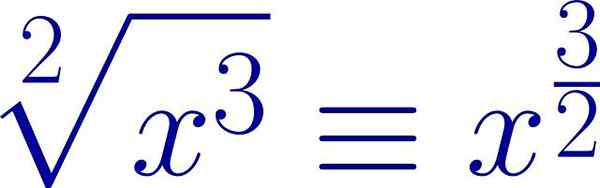Príklad radikálneho výrazu napísaného vo forme frakčného exponentu. Koreňový index je menovateľ exponentov, zatiaľ čo výkonom vysielania je čitateľ. Zdroj: Wikimedia Commons.

Týmto spôsobom sa môžu použiť rovnaké vlastnosti, ktoré sa vzťahujú na právomoci, môžu byť použité v prípade radikálov.

Pre hodnoty patriace do súboru reálnych čísel sú tieto vlastnosti nasledujúce:

1. Radikálny produkt rovnakého indexu

V produkte dvoch (alebo viacerých) radikálov toho istého indexu sa subradické sumy vynásobia, čo udržiava index:

2. Radikálny kvocient toho istého indexu

Kvocient medzi n-the koreňom „A“ a n-eme „B“, ktorý je B ≠ 0, sa rovná koreňu kvocientu medzi „A“ a „B“:

3. Koreň

Ak chcete nájsť koreň N-EMEASY z M-Eme sumy „A“, subradickú sumu je napísaná pod koreňom, ktorého index je produkt medzi „N“ a „M“:

Tento postup sa ľahko rozšíri na po sebe nasledujúce vnorené korene. Výsledný koreňový index je produktom všetkých indexov, ako je tento:

4. Koreňová sila

N-to, zdvihnuté k moci m, vyjadruje subradickú sumu uvedenú silu:

Konkrétne prípady:

1) Áno n = m, Koreňová značka zmizne a základňa zostane zvýšená na napájanie 1:

Čo je platné pre ≥ 0. Všeobecne platí, že ak je koreňový index párne číslo, máte:

(Pozri príklady neskôr)

2) Áno m> n, Frakcia m/n je nesprávna a koreň sa môže zjednodušiť, napríklad hľadať frakčný ekvivalent s m/n tak, aby čitateľ a menovateľ boli navzájom bratranci alebo prepisovali subradickú sumu a uplatňovali niektoré z tu opísané vlastnosti.

Môže vám slúžiť: hranoly a pyramídy

(Pozri príklady neskôr)

5. Zosilnenie

Radikál môže byť zosilnený faktorom Otázka, Ak index koreňov, ako aj sila subradického množstva, vynásobte uvedeným faktorom a táto operácia neznamená modifikáciu výsledku. Preto:

Za predpokladu, že ≥ 0, keď je rovnomerne.

6. Zavedenie faktora v radikáli

Ak pozitívny faktor „B“ vynásobí radikál, môže v ňom prejsť, ak stúpa na rovnaký koreňový index. V tom prípade:

7. Súčet a odčítanie radikálov

Radikály môžu pridať a odčítať, pokiaľ sú rovnakým indexom a majú rovnaké subradickú sumu.

Ak sú dva alebo viac radikálnych rovnakých indexov a subradikálneho množstva, hovorí sa, že sú Podobné radikály.

Napríklad nasledujúce radikály sú podobné:

Namiesto toho tieto radikály nie sú podobné, pretože nemajú rovnakú subradickú sumu:

Ani tieto dve podobné:

Pretože radikálny index nie je rovnaký.

Podobné radikály sa môžu znížiť na jeden a pridať alebo odčítať koeficienty, ktoré ich sprevádzajú.

Príklady radikálnych vlastností

Príklad 1

Aká je hodnota nasledujúcich koreňov?

Druhý koreň 32 nájdete priamo pomocou kalkulačky. Jeho hodnota je:

Podporné body naznačujú, že existujú nekonečné desatinné miesto.

Ak radšej nepracujete s desatinnými číslami, druhá druhá koreň 32 sa dá vypočítať aj rozložením 32 v hlavných faktoroch:

32 = 2⁵

Týmto spôsobom sa pri výmene získa:

Môže vám slúžiť: DETIVORY 8: Čo sú a ľahké vysvetlenie

Napísaný ako zlomkový exponent:

Frakcia 5/2 je nesprávna, takže radikál sa dá zjednodušiť pomocou vlastností právomocí:

Teraz uplatňovanie nehnuteľnosti 1 vyššie:

Preto:

Po jeho časti:

Pretože (−2)³ = −8.

Podľa nehnuteľnosti 4:

A nakoniec, druhá druhá koreň −8 neexistuje v súbore reálnych čísel, hoci v zložitých číslach.

Príklad 2

Vzhľadom na nasledujúcu operáciu:

Je možné znížiť výsledok?

Za predpokladu, že radikály sú podobné, je možné ich znížiť, ale preto musia mať rovnaký index a rovnaké subradické množstvo. V predchádzajúcom príklade bolo vidieť, že:

Analogický postup sa dá použiť na písanie prvého pridania, takže subradickú sumu sa rovná 2:

Tento radikál je podobný ako predchádzajúci. Pokiaľ ide o druhú odmocninu 81, to je 9, preto:

Príklad 3

Aké vlastnosti sú potrebné na uplatnenie na vykonanie tejto operácie?

Musíme aplikovať vlastnosti 3 a 5, ktoré sú korene koreňa a zavedenie radikálnej hodnoty. Po prvé, vlastnosť 5 sa uplatňuje na predstavenie „X“, ktorý je mimo najvnútornejšej koreňov:

A teraz je výraz pripravený uplatniť vlastnosť 3 a vynásobiť príslušné indexy každého radikálu:

Odkazy

1. Gonzales, D. 2011. Základná algebra: teória a prax. Druhý. Vydanie.
2. Haeussler, e. 2012. Predbežné vyfarbenie. 1. Vydanie. Pearson.
3. Khan Acadaem. Exponenty a radikály. Získané z: Khanacademy.orgán.
4. Larson, R. 2012. Predbežné vyfarbenie. 8. Vydanie. Učenie sa.
5. Stewart, J. 2007. Matematika na výpočet. 5. Vydanie. Učenie sa.