Matematika

Obmedzte vlastnosti (s príkladmi)

3217
20
Tomáš Klapka

Ten Limitné vlastnosti Sú súborom algebraických pravidiel a postupov používaných na ich určenie. Koncept limitu je nevyhnutný na výpočet a nájdenie jej hodnoty nemusí byť zložitá úloha za predpokladu, že jej vlastnosti sa s ľahkosťou zaobchádza.

Nižšie je uvedený zoznam najdôležitejších, sprevádzaných príkladmi aplikácie.

Limity a jeho vlastnosti sú základom výpočtu. Na obrázku je uvedený veľmi špeciálny limit: Derivát funkcie F (x)

Nech B, C, N, A a B Real Numbers and F a g Takéto funkcie, ktoré overujú nasledujúce:

$\lim_x\rightarrow cf(x)=A$
$\lim_x\rightarrow cg(x)=B$

Potom máte nasledujúce vlastnosti:

1. Limit priameho výmeny

V prvom prípade limit funkcie F, keď sa x → c môže vypočítať priamo nahradiť x = c vo funkcii. Ak funkcia existuje pri x = c, potom je limit:

$\lim_x \rightarrow c f(x)=f(c)$ Ale nie nevyhnutne táto funkcia musí byť definovaná pri x = c, takže limit existuje. Zámerom je pristupovať k toľko, koľko chcete k hodnote x = c, a zistiť, čo sa v tomto prípade stane s funkciou.

Príklad

Nájdite limit f (x) = x² Keď x → 4

Riešenie

Limit sa rieši jednoducho nahradením x = 4 v f (x) = x², Pretože pri vykonávaní operácie nie sú žiadne nepríjemnosti:

$\lim_x\rightarrow 4x^2=4^2=16$ 2. Jedinečnosť limitu

Ak limit funkcie f (x), keď x → c existuje a má hodnotu l, uvedený limit je jedinečný.

Preto bočné limity, ktoré sú obmedzeniami, keď x → c^- (Prečítajte si „X má tendenciu C zľava“) a keď x → C⁺(Znie „x má tendenciu C napravo“), existujú a majú rovnakú hodnotu l, aj keď funkcia nie je definovaná v x = c.

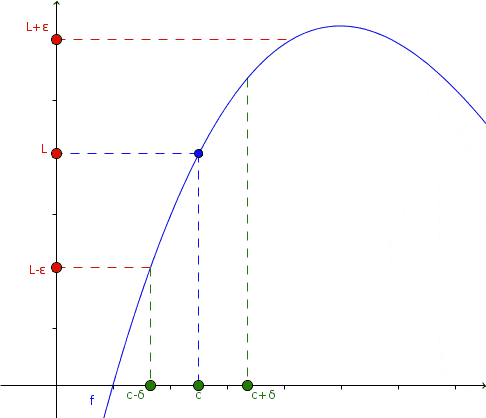V tejto animácii je uvedený koncept limitu: keď X má tendenciu k určitej hodnote C, ktorá sa blíži vľavo aj vpravo, hodnota funkcie má tendenciu L k L k L. Nie nevyhnutne funkcia je definovaná v x = c. Zdroj: Wikimedia Commons.

V animácii je tento prístup pozorovaný a čo sa stane s funkciou v takom prípade: či sa blíži vľavo a vpravo k x = c, hodnota funkcie je zase blízko L.

Môže vám slúžiť: minimálne štvorce

Matematicky vyjadruje týmto spôsobom:

$\lim_x\rightarrow c^-f(x)=\lim_x\rightarrow c^+f(x)=\lim_x\rightarrow cf(x)=L$ Bočné limity umožňujú vedieť, kedy existuje alebo nie, pretože ak neexistujú alebo ak sa líšia, je isté, že limit funkcie, keď X → C neexistuje.

Príklad

Vypočítajte limit f (x), keď x → 1, ak existuje, kde f (x) je daný:

Riešenie

Toto je funkcia podľa častí alebo definovaná na kúsky, ktoré pozostávajú z riadku 4 -x pre hodnoty x < 1 y en la parábola 4 - x² Keď sa x rovná 1 alebo väčšie ako 1.

Môžeme sa priblížiť x = 1 zľava, v tomto prípade sa berie časť funkcie, ktorá je platná pre X<1:

Pretože bočné limity sú rovnaké, z toho vyplýva, že limit funkcie, keď x → 1 existuje a má hodnotu 3.

3. Konštantný

Limit konštanty je hodnota uvedenej konštanty bez ohľadu na hodnotu, ktorej premenná má tendenciu:

$\lim_x\rightarrow cb=b .$

Príklad

Vypočítať:

$\lim_x\rightarrow 1\pi$ Riešenie

$\lim_x\rightarrow 1\pi= \pi$

4. Limit funkcie identity

Ak f (x) = x, vždy sa splní:

$\lim_x\rightarrow cx=c$

Príklad

Vypočítať:

$\lim_x\rightarrow 2x$ Riešenie

$\lim_x\rightarrow 2x=2$

5. Limit produktu konštanty funkciou

V tomto prípade konštanta vychádza z limitu a presúva sa, aby ju vynásobila, takto:

$\lim_x\rightarrow c\left [b\cdot f(x) \right ]=b\cdot \lim_x\rightarrow c f(x)=b\cdot A$ Príklad

Vypočítajte, ak existuje, nasledujúci limit:

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]$ Riešenie

Konštanta 5 je vonku vynásobená limitu a uplatňuje sa vlastnosť výmeny:

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]=5\cdot \lim_x\rightarrow -2 x^3=5\cdot (-2)^3=-40$

6. Limit

Limit súčtu dvoch funkcií F a g Je to súčet limitov:

$\lim_x\rightarrow c\left [ f(x)+g(x) \right ]=\lim_x\rightarrow c f(x)+\lim_x\rightarrow cg(x)=A+B$

Príklad

Ak existuje, nájdete nasledujúci limit:

Môže vám slúžiť: Sada Teória: Charakteristiky, prvky, príklady, cvičenia

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ]$ Riešenie

Vlastnosť súčtu limitov sa uplatňuje ako prvá a potom priama výmena, pretože operácie nepredstavujú ťažkosti:

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ] = \lim_\theta \rightarrow \pi cos\: \: \theta + \lim_\theta \rightarrow \pisen\: \: \theta=cos\: \pi +sen\: \pi =-1$

7. Limit odčítania

V prípade limitu odčítania dvoch funkcií postupujte analogickým spôsobom, že pre súčet: limit odčítania je odčítanie limitov:

$\lim_x\rightarrow c \left [f(x) - g(x) \right ]=A-B$

Príklad

Vypočítajte nasledujúci limit:

$\lim_x \rightarrow 0 [sec\: x - e^x ]$ Riešenie

Vlastnosť limitu odčítania dvoch funkcií sa použije a potom priama výmena, pretože všetky operácie sa dajú vykonať bez problémov:

$\lim_x \rightarrow 0 [sec\: x - e^x ]=\lim_x \rightarrow 0 sec\: x -\lim_x \rightarrow 0 e^x = sec\: 0-e^0=1-1=0$

8. Limit produktu

Limit produktu dvoch funkcií F a g Je to produkt limitov:

$\lim_x \rightarrow c [f(x)\cdot g(x) ]=\lim_x \rightarrow c f(x) \cdot \lim_x \rightarrow c g(x) = A\cdot B$ Príklad

Vypočítajte tento limit:

$\lim_x \rightarrow 0 cos\: x\cdot (1-x^2^)$

Riešenie

$\lim_x \rightarrow 0 cos\: x\cdot (1-x^2^)=\lim_x \rightarrow 0 cos\: x\cdot \lim_x \rightarrow 0 (1-x^2^)=cos\: 0\cdot (1-0^2)=1$

9. Pomer kvocientu

Limit pomeru dvoch funkcií F a g Je to kvocient limitov za predpokladu, že limit g (x), keď sa x → c líši od 0, pretože rozdelenie o 0 nie je definované. Tak:

$\lim_x \rightarrow c \left [ \fracf(x)g(x) \right ]=\frac\lim_x \rightarrow c f(x)\lim_x \rightarrow c g(x)=\fracAB; \: \: \textupcon\: B\neq 0$

Príklad

Vypočítajte, ak existuje, hodnota nasledujúceho limitu:

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]$ Riešenie

V prvom rade sa uplatňuje vlastnosť Limit Vlastnosti, aby sa získal kvocient limitov:

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]=\frac\lim_x \rightarrow -3 2x-6\lim_x \rightarrow -3 x^2+5$

Vlastnosť výmeny sa teraz uplatňuje na nájdenie každého limitu:

$\lim_x \rightarrow -3 2x-6=2\cdot (-3)-6=-12$ $\lim_x \rightarrow -3 x^2+5= (-3)^2+5=14$

A keďže b ≠ 0, požadovaný limit je kvocient A/B:

$\lim_x \rightarrow -3 \frac2x-6x^2+5=\frac-1214=\frac-67$

10. Obmedzenie

Limit sily exponentu N je rovnocenný s limitom zvýšenou na uvedenú moc takto:

$\lim_x \rightarrow c \left [f(x) \right ]^n=\left [\lim_x \rightarrow c f(x) \right ]^^n$ Prípad 1: Limit X Power

Ak máte napríklad limit výkonu X, výsledky:

$\lim_x \rightarrow c x^n=\left [\lim_x \rightarrow c x \right ]^n$

Podľa nehnuteľnosti 4 je tento limit:

Môže vám slúžiť: numerické analógie: typy, aplikácie a cvičenia

$\lim_x \rightarrow c x^n=c^n$

Prípad 2: Koreňový limit

Tento koreň je možné napísať vo forme frakčného exponentu, preto:

$\lim_x \rightarrow c \sqrt[n]f(x)=\sqrt[n]\lim_x \rightarrow c f(x)$

Dôležitý: Ak je koreňový index rovnomerne, je potrebné, aby limit f (x), keď x → c je väčší alebo rovný 0, pretože neexistujú žiadne skutočné páry záporných množstiev.

Príklady

Určite, uplatňujte predchádzajúce vlastnosti, tieto limity, ak existujú:

$a)\: \lim_x \rightarrow -2 (x+5)^^3$

$b)\: \lim_x \rightarrow 3 \sqrt2x-1$

Roztok

Vlastníctvom limitu moci a priamej substitúcie sa získa:

$\lim_x \rightarrow -2 (x+5)^^3= \left [\lim_x \rightarrow -2 (x+5) \right ]^3=(-2+5)^3=27$

Riešenie B

$\lim_x \rightarrow 3 \sqrt2x-1=\sqrt\lim_x \rightarrow 3 \left (2x-1 \right )=\sqrt(2\cdot 3-1)=\sqrt5$

jedenásť. Obmedzenie

Na nájdenie limitu základného exponenciálneho B a exponentu F (x), musí sa základ funkcie F (x) zvýšiť takto:

$\lim_x \rightarrow c \left [b^f(x) \right ]=b^\lim_x \rightarrow cf(x)$

Príklad

Zistite, či existuje nasledujúci limit:

$\lim_x \rightarrow 1 \left [e^x^^2 \right ]$ Riešenie

V tomto limite je základňa číslo E a funkcia f (x) = x², Preto musíte najskôr vypočítať limit X² Keď X má tendenciu 1:

$\lim_x \rightarrow 1 x^2=1^^2=1$

Potom sa uplatňuje vlastnosť exponenciálneho limitu:

$\lim_x \rightarrow 1 e^^x^2=e^^1=e$

12. Limit funkcie exponenciálneho potenciálu

Limit, keď x → c funkcie f (x), ktorý je zase zvýšený na inú funkciu g (x), sa vyjadruje:

$\lim_x \rightarrow c \left [f(x)^g(x) \right ]=\left [\lim_x \rightarrow c f(x) \right ]^\lim_x \rightarrow c g(x)$

Príklad

Vypočítajte nasledujúci limit, ak existuje:

$\lim_x \rightarrow -1 (x-1)^^2x$

Riešenie

Na použitie predchádzajúcej vlastnosti sú najskôr identifikované F (x) = x-1 a g (x) = 2x a potom sa vypočítajú príslušné limity:

$\lim_x \rightarrow -1 (x-1)=-1-1=-2$

$\lim_x \rightarrow -1 2x=2\cdot (-1)=-2$ Konečne:

$\lim_x \rightarrow -1 (x-1)^2x=\left [\lim_x \rightarrow -1 (x-1) \right ]^\lim_x \rightarrow -1 2x=(-2)^-2=\left (\frac1-2 \right )^2=\frac14$ Odkazy

Ayres, f. 2000. Kalkulácia. 5ed. MC Graw Hill.
Leithold, L. 1992. Výpočet analytickou geometriou. Harla, s.Do.
Bezplatné matematické texty. Limity. Získané z: matematiky.Libretexts.orgán.
Matematický. Zákony a obmedzujú nehnuteľnosti. Získané z: Matemovil.com.
Larson, R. 2010. Výpočet premennej. 9NA. Vydanie. McGraw Hill.
Purcell, e. J., Varberg, D., & Rigdon, s. A. (2007). Kalkulácia. Mexiko: Pearson Education.
Vesmír. Limitné vlastnosti. Získané z: Universoformulas.com

Obmedzte vlastnosti (s príkladmi)

1. Limit priameho výmeny

Príklad

Riešenie

2. Jedinečnosť limitu

Príklad

Riešenie

3. Konštantný

Príklad

Riešenie

4. Limit funkcie identity

Príklad

Riešenie

5. Limit produktu konštanty funkciou

Príklad

Riešenie

6. Limit

Príklad

Riešenie

7. Limit odčítania

Príklad

Riešenie

8. Limit produktu

Príklad

Riešenie

9. Pomer kvocientu

Príklad

Riešenie

10. Obmedzenie

Prípad 1: Limit X Power

Prípad 2: Koreňový limit

Príklady

Roztok

Riešenie B

jedenásť. Obmedzenie

Príklad

Riešenie

12. Limit funkcie exponenciálneho potenciálu

Príklad

Riešenie

Odkazy

Najlepšie články

Flóra a fauna reprezentatívnych druhov Tucumánu

Tucumánova flóra a fauna sú zastúpené druhmi ako ružový lapmach. Tucumán je druhá najmenšia provinci...

Moorský nový pôvod, charakteristiky, zástupcovia a diela

Moorský román je literárny žáner, ktorý sa zaoberá vzťahmi medzi rascami a kresťanmi v Španielsku 16...

$\lim_x\rightarrow 4x^2=4^2=16$ 2. Jedinečnosť limitu

$\lim_x\rightarrow 1\pi$ Riešenie

$\lim_x\rightarrow 2x$ Riešenie

$\lim_x\rightarrow c\left [b\cdot f(x) \right ]=b\cdot \lim_x\rightarrow c f(x)=b\cdot A$ Príklad

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]$ Riešenie

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ]$ Riešenie

$\lim_x \rightarrow 0 [sec\: x - e^x ]$ Riešenie

$\lim_x \rightarrow c [f(x)\cdot g(x) ]=\lim_x \rightarrow c f(x) \cdot \lim_x \rightarrow c g(x) = A\cdot B$ Príklad

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]$ Riešenie

$\lim_x \rightarrow c \left [f(x) \right ]^n=\left [\lim_x \rightarrow c f(x) \right ]^^n$ Prípad 1: Limit X Power

$\lim_x \rightarrow 1 \left [e^x^^2 \right ]$ Riešenie

$\lim_x \rightarrow -1 (x-1)^2x=\left [\lim_x \rightarrow -1 (x-1) \right ]^\lim_x \rightarrow -1 2x=(-2)^-2=\left (\frac1-2 \right )^2=\frac14$ Odkazy