Sum asociatívna vlastnosť, násobenie, príklady, cvičenia

Ten asociatívna vlastnosť Z tejto sumy predstavuje asociatívnu povahu operácie dodáva v rôznych matematických množinách. Vzťahuje sa na tri (alebo viac) prvkov týchto súborov nazývaných A, B a C, takže je vždy splnený:

a + (b + c) = (a + b) + c

Týmto spôsobom je zaručené, že bez ohľadu na to, ako zoskupovať vykonávanie operácie, výsledok je rovnaký.

postava 1. Pri aritmetických a algebraických operáciách používame asociatívnu vlastnosť súčtu mnohokrát. (Výkres: Freepik Zloženie: f. Zapata)

Je však potrebné poznamenať, že asociatívne vlastníctvo nie je synonymom komutatívneho majetku. To znamená, že vieme, že poradie pridaní nemení súčet alebo že poradie faktorov nemení produkt. Takže pre sumu, ktorú môžete napísať takto: a + b = b + a.

Avšak v asociatívnom vlastníctve je to iné, pretože poradie prvkov, ktoré sa majú pridať. Čo znamená, že na tom nezáleží na prvom mieste (b+c) a k tomuto výsledku sa pridá, začať sa pridávať do B a k výsledku pridať c.

Mnoho dôležitých operácií, ako je suma. Napríklad pri odčítaní skutočných čísel sa stáva, že:

A - (b - c) ≠ (a - b) - c

ÁNO A = 2, B = 3, C = 1, potom:

2- (3 - 1) ≠ (2 - 3) - 1

0 ≠ -2

[TOC]

Asociatívna vlastnosť násobenia

Ako sa stalo pre sumu, asociatívna vlastnosť násobenia naznačuje, že:

a ˟ (b ˟ c) = (a ˟ b) ˟ c

Môže vám slúžiť: súčet polynómov, ako sa to robí, príklady, cvičenia

V prípade súboru reálnych čísel je ľahké overiť, či je to vždy. Napríklad pri použití hodnôt a = 2, b = 3, c = 1 musíte:

2 _˟ (3 _˟ 1) = (2 _˟  3) _˟ 1 → 2 _˟ 3 = 6 _˟ 1

6 = 6

Skutočné čísla spĺňajú asociatívnu vlastnosť súčtu aj násobenia. Na druhej strane, v inej sade, podobne ako v prípade vektorov, je suma asociatívna, ale krížový produkt alebo vektor.

Aplikácie asociatívneho vlastníctva násobenia

Výhoda, že operácie, v ktorých je splnená asociatívna vlastnosť, sa splnia najpohodlnejším spôsobom. To výrazne uľahčuje rozlíšenie.

Napríklad predpokladajme, že v malej knižnici sú 3 police s 5 zábavou. V každej zábave je 8 kníh. Koľko kníh je celkovo?

Môžeme vykonať operáciu nasledovne: Celkom knihy = (3 x 5) x 8 = 15 x 8 = 120 kníh.

Alebo tak: 3 x (5 x 8) = 3 x 40 = 120 kníh.

Obrázok 2. Aplikácia asociatívnej vlastnosti násobenia je výpočet počtu kníh na každej polici. Obrázok vytvorený f. Zapata.

Príklady

-V súboroch prírodných, celých, racionálnych, skutočných a komplexných čísel sa splní asociatívna vlastnosť súčtu a násobenia.

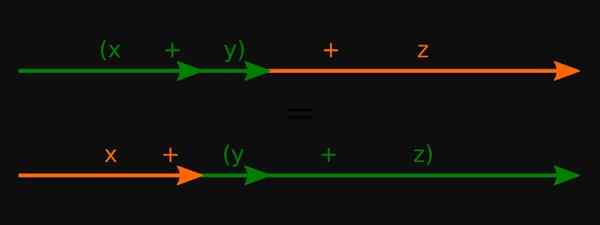Obrázok 3. Pokiaľ ide o skutočné čísla, asociatívny majetok sumy je splnený. Zdroj: Wikimedia Commons.

-V prípade polynómov sa uplatňujú aj v týchto operáciách.

-V prípadoch odčítania operácií, rozdelenia a exponencie nie je asociatívny majetok splnený v reálnych číslach alebo polynómoch.

Môže vám slúžiť: ortoedro: vzorce, oblasť, objem, diagonálne, príklady

-V prípade matíc je asociatívna vlastnosť splnená pre súčet a násobenie, hoci v druhom prípade nie je komunita splnená. To znamená, že vzhľadom na matice A, B a C je pravda, že:

(A x b) x c = a x (b x c)

Ale ... a x b ≠ b x a

Asociatívne vlastníctvo vo vektoroch

Vektory tvoria inú množinu ako reálne čísla alebo zložité čísla. Operácie definované pre súbor vektorov sú trochu odlišné: existuje súčet, odpočítanie a tri typy produktov.

Súčet vektorov spĺňa asociatívnu vlastnosť, ako aj čísla, polynómy a matice. Pokiaľ ide o skalárne výrobky, lezenie vektorom a krížom, ktoré sa vyrábajú medzi vektormi, nestretáva sa, ale skalárny produkt, ktorý je ďalším druhom operácie medzi vektormi, ho spĺňa, berúc do úvahy nasledujúce:

-Produkt skalárneho pre vektor má za následok vektor.

-A lezením na dva vektory je to skalár.

Preto vzhľadom na vektory vložka, alebo a W, A navyše skalárny λ, je možné napísať:

-Súčet vektorov: vložka +(alebo + W ) = (vložka + alebo) + W

-Skalárny produkt: λ (vložka • alebo ) = (λvložka) • alebo

Ten je možný vďaka čomu vložka • alebo Je to skalár a λvložka Je to vektor.

Avšak:

vložka × (alebo × W ) ≠ (vložka × alebo)×W

Polynómová faktorizácia zoskupením výrazov

Táto aplikácia je veľmi zaujímavá, pretože ako je uvedené vyššie, asociatívna vlastnosť pomáha vyriešiť určité problémy. Súčet monomálov je asociatívny a to sa dá použiť na faktor, keď sa zjavný spoločný faktor neobjaví na prvý pohľad.

Môže vám slúžiť: konvexný polygón: definícia, prvky, vlastnosti, príklady

Predpokladajme napríklad, že sa vyžaduje faktor: X³ + 2X² + 3X +6. Tento polynóm nemá spoločný faktor, ale pozrime sa, čo sa stane, ak je zoskupený týmto spôsobom:

X³ + 2x² + 3x +6 = (x³ + 2x²) + (3x +6)

Prvá zátvorka má ako spoločný faktor X²:

X³ + 2X² = X² (x+2)

V druhom je spoločný faktor 3:

3x +6 = 3 (x + 2)

Tak:

X³ + 2X² + 3X +6 = X²(x+ 2)+ 3 (x+ 2)

Teraz existuje zjavný spoločný faktor, ktorý je x+2:

X²(x+ 2)+ 3 (x+ 2) = (x+ 2) (x²+3)

Cvičenia

- Cvičenie 1

Budovanie školy má 4 poschodia a v každom je tu 12 tried s 30 stopami vo vnútri. Koľko stolov má celkom škola?

Riešenie

Tento problém sa vyrieši uplatňovaním asociatívnej vlastnosti násobenia, pozrime sa:

Celkový počet stolov = 4 poschodia x 12 tried /podlaha x 30 stolov /učebňa = (4 x 12) x 30 stolov = 48 x 30 = 1440 stolov.

O, ak sa uprednostňuje: 4 x (12 x 30) = 4 x 360 = 1440 stolov

- Cvičenie 2

Vzhľadom na polynómy:

A (x) = 5x³ + 2x² -7x + 1

B (x) = x⁴ +6x³ -5x

C (x) = -8x² +3x -7

Použite asociatívnu vlastnosť súčtu na nájdenie (x) + b (x) + c (x).

Riešenie

Prvé dve môžu byť zoskupené a výsledok pridá tretí:

A (x) + b (x) = [5x³ + 2x² -7x + 1] + [x⁴ +6x³ -5x] = x⁴ + 11x³+ 2x² -12x +1

Okamžite sa pridá polynóm C (x):

[X⁴ + 11x³+ 2x² -12x +1] + [-8x² +3x -7] = x⁴ + 11x³ - 6x² -9x -6

Čitateľ môže overiť, či je výsledok rovnaký, ak je vyriešený podľa možnosti A (x) + [b (x) + c (x)]]]]]]]]]]]]]]]]]]]]]]]]].

Odkazy

1. Jiménez, r. 2008. Algebra. Sála.
2. Matematika je zábava. Komunikačné, asociatívne a okresné zákony. Získané z: Mathisfun.com.
3. Matematický sklad. Definícia asociatívneho majetku. Obnovené z: Mathwarehouse.com.
4. Vedecký. Asociatívna a komutatívna vlastnosť pridávania a násobenia (s príkladom). Obnovené z: vedeckých.com.
5. Wikipedia. Asociatívna vlastnosť. Zdroj: In.Wikipedia.orgán.